|
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Задачи-2(11 класс)
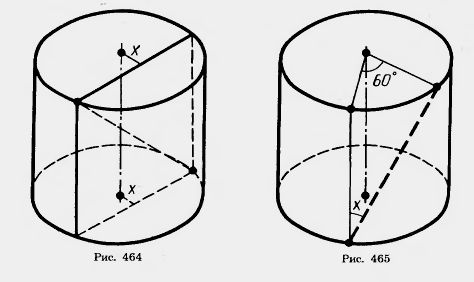
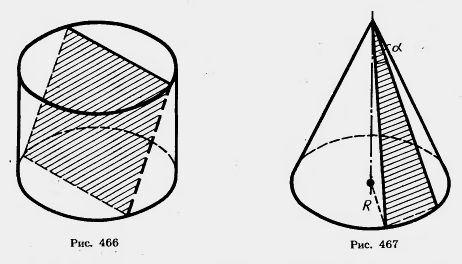
Задачи 2.Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра. 3.Высота цилиндра 6 см, радиус основания 5 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее. 4.Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси (рис. 464). 5.Высота цилиндра 6 дм, радиус основания 5 дм. Концы отрезка АВ, равного 10 дм, лежат на окружностях обоих оснований. Найдите кратчайшее расстояние от него до оси. 6.В равностороннем цилиндре (диаметр равен высоте цилиндра) точка окружности верхнего основания соединена с точкой окружности нижнего основания. Угол между радиусами, проведенными в эти точки, равен 60°. Найдите угол X между проведенной прямой и осью цилиндра (рис. 465). 7. В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра. 10. Образующая конуса I наклонена к плоскости основания под углом 30°. Найдите высоту. 11. Радиус основания конуса R. Осевым сечением является прямоугольный треугольник. Найдите его площадь. 12. В равностороннем конусе (в осевом сечении правильный треугольник) радиус основания R. Найдите площадь сечения, проведенного через две образующие, угол между которыми равен 13. Высота конуса 20, радиус его основания 25. Найдите площадь сечения, проведенного через вершину, если расстояние от него до центра основания конуса равно 12. 14. Радиус основания конуса R, а образующая наклонена к плоскости основания под углом 15. Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота Н. 16. Высота конуса Н. На каком расстоянии от вершины надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания? 17. Через середину высоты конуса проведена прямая параллельно образующей I. Найдите длину отрезка прямой, заключенного внутри конуса.
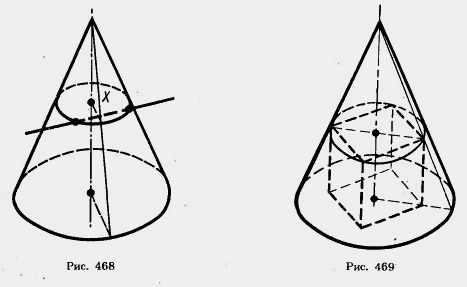
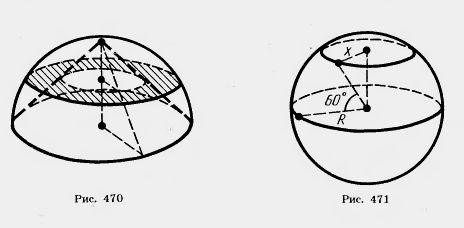
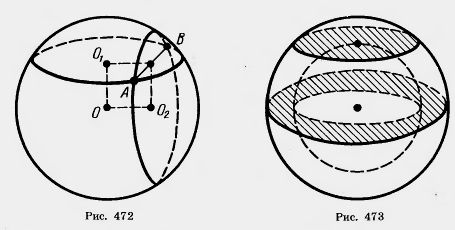
18*. Образующая конуса 13 см, высота 12 см. Конус пересечен прямой, параллельной основанию; расстояние от нее до основания равно 6 см, а до высоты — 2 ом. Найдите отрезок прямой, заключенный внутри конуса (рис. 468). 19. Радиусы оснований усеченного конуса 3 м и 6 м, высота 4 м. Найдите образующую. 20. Радиусы оснований усеченного конуса R и r, образующая наклонена к основанию под углом 45°. Найдите высоту. 21. Образующая усеченного конуса равна 2а и наклонена к основанию под углом 60°. Радиус одного основания вдвое больше радиуса другого основания. Найдите радиусы. 22. Радиусы оснований усеченного конуса 3 дм и 7 дм, образующая 5 дм. Найдит^ площадь осевого сечения. 23. Площади оснований усеченного конуса 4 дм2 и 16 дм2. Через середину высоты проведена плоскость, параллельная основаниям. Найдите площадь сечения. 24. Площади оснований усеченного конуса Мит. Найдите площадь среднего сечения, параллельного основаниям. 25. У пирамиды все боковые ребра равны. Докажите, что она является вписанной в некоторый конус. 26*. В конусе даны радиус основания R и высота Н. Найдите ребро вписанного в него куба (рис. 469). 27*. В конусе даны радиус основания R и высота Н. В него вписана правильная треугольная призма, у которой боковые грани — квадраты. Найдите ребро призмы. 28. Полушар и вписанный в него конус имеют общее основание и общую высоту. Через середину высоты проведена плоскость, параллельная основанию. Докажите, что площадь сечения, заключенного между боковой поверхностью конуса и поверхностью полушара, равна половине площади основания (рис. 470). 29. Шар, радиус которого 41 дм, пересечен плоскостью на расстоянии 9 дм от центра. Найдите площадь сечения. 30. Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга? 31. Радиус шара R. Через конец радиуса проведена плоскость под углом 60° к нему. Найдите площадь сечения. 32. Радиус земного шара R. Чему равна длина параллели, если ее широта 60° (рис, 471)? 33. Город N находится на 60° северной широты. Какой путь совершает этот пункт в течение 1 ч вследствие вращения Земли вокруг своей оси? Радиус Земли принять равным 6000 км. 34. На поверхности шара даны три точки. Прямолинейные расстояния между ними 6 см, 8 см, 10 см. Радиус шара 13 см. Найдите расстояние от центра до плоскости. Проходящей через эти точки. 35. Диаметр шара 25 см. На его поверхности даны точка А и окружность, все точки которой удалены (по прямой) от А на 15 см. Найдите радиус этой окружности. . Радиус шара 7 см. На его поверхности даны две равные окружности, имеющие общую хорду длиной 2 см. Найдите радиусы окружностей, зная, что их плоскости перпендикулярны (рис. 472). 37. Дан шар радиуса R. Через одну точку его поверхности проведены две плоскости: первая — касательная к шйру, вторая — под углом 30° к первой. Найдите площадь сечения.
39. Шар радиуса R касается всех сторон правильного треугольника со стороной а. Найдите расстояние от центра шара до плоскости треугольника. 40. Стороны треугольника 13 см, 14 см и 15 см. Найдите расстояние от плоскости треугольника до центра шара, касающегося всех сторон треугольника. Радиус шара 5 см. 41. Диагонали ромба 15 см и 20 см. Шаровая поверхность касается всех его сторон. Радиус шара 10 см. Найдите расстояние от центра шара до плоскости ромба. 42. Через касательную к поверхности шара проведены две взаимно перпендикулярные плоскости, пересекающие шар по кругам радиусов r1 и r2. Найдите радиус шара R. 43. Шар радиуса R вписан в усеченный конус. Угол наклона образующей к плоскости нижнего основания конуса равен а. Найдите радиусы оснований и образующую усеченного конуса. 44. Два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности. 45. Радиусы шаров равны 25 дм и 29 дм, а расстояние между их центрами 36 дм. Найдите длину линии, по которой пересекаются их поверхности. 46. Найдите радиус шара, описанного около куба с ребром а. 47. Докажите, что центр шара, описанного около правильной пирамиды, лежит на ее оси. 48. Докажите, что центр шара, вписанного в правильную пирамиду, лежит на ее высоте. 49. Найдите радиус шара, описанного около правильного тетраэдра с ребром а. 50. В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен 51*. В шар радиуса R вписана правильная треугольная пирамида с плоскими углами 52. Правильная n-угольная призма вписана в шар радиуса R. Ребро основания призмы равно 1) n = 3; 2) n = 4; 3) n = 6. 53. Сторона основания правильной n-угольной пирамиды равна а, двугранный угол при основании равен 54. Найдите радиус шара, описанного около правильной n-угольной пирамиды, если сторона основания равна а, а боковое ребро наклонено к плоскости основания под углом
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: