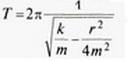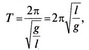Гіпермаркет Знань>>Фізика і астрономія>>Фізика 11 клас>> Фізика: Коливальний рух. Вільні коливання. Амплітуда, період, частота. Математичний маятник. Коливання вантажу на пружині

КОЛИВАЛЬНИЙ РУХ. ВІЛЬНІ КОЛИВАННЯ. АМПЛІТУДА, ПЕРІОД, ЧАСТОТА. МАТЕМАТИЧНИЙ МАЯТНИК. КОЛИВАННЯ ВАНТАЖУ НА ПРУЖИНІ

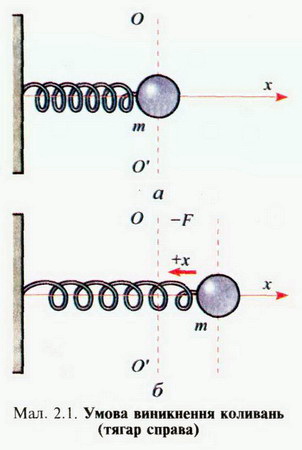
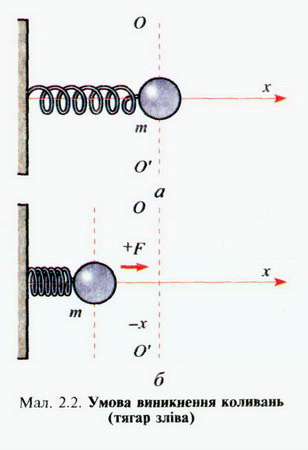
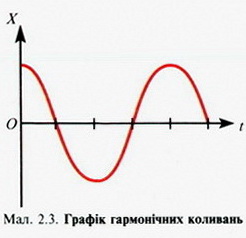
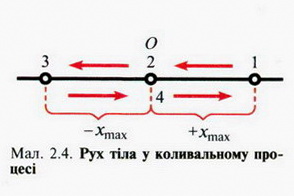
МЕХАНІЧНІ КОЛИВАННЯ І ХВИЛІ

Коливання — це будь-який процес, під час якого стан тіла або фізичної системи тіл повторюється через певні інтервали часу.

Коливання — найпоширеніша форма руху в навколишньому світі та техніці. Коливаються дерева під дією вітру, поршні у двигуні автомобіля тощо. Ми можемо розмовляти і чути звуки завдяки коливанням голосових зв'язок, повітря і барабанних перетинок; коливається серце. Це все — приклади механічних коливань. Світло — це також коливання, але електромагнітні. За допомогою електромагнітних коливань, які поширюються в просторі, можна здійснювати радіозв'язок, радіолокацію, передавати телевізійні передачі, а також лікувати деякі хвороби. Перелічити всі види коливань неможливо.

Наведені приклади механічних і електромагнітних коливань з першого погляду мають мало спільного. Проте під час їх дослідження було виявлено цікаву закономірність: різні за фізичною природою коливання описуються однаковими математичними рівняннями, що значно полегшує їх вивчення.

Коливання бувають періодичними і неперіодичними. Найцікавішими є дослідження періодичних коливань.

Періодичним називають такий процес, за якого величина, що коливається взята у будь-який момент часу, через певний інтервал часу Т матиме те саме значення.

Коливання — найпоширеніша форма руху в навколишньому світі

Різні за фізичною природою коливання описуються однаковими математичними рівняннями, що значно полегшує їх вивчення

Математичне визначення періодичної функції таке: функцію f (t) називають періодичною з періодом Т, якщо f (t+T) = f (t) за будь-яких значень змінної t.

Дослідження коливань у техніці — надзвичайно важлива справа. Деякі коливання можна виявити лише за допомогою спеціальних датчиків. Такими є, наприклад, коливання різних споруд, корпусів і деталей машин, літальних апаратів тощо. Датчики сприймають коливання, перетворюють їх переважно на електричні сигнали, які реєструються вимірювальними приладами, електронними осцилографами та іншими пристроями.

Найпростішими є гармонічні коливання

Найпростішими механічними коливаннями є так звані гармонічні коливання. Гармонічними вважають коливаня, за яких зміни фізичних величин з часом відбуваються за законами змін синуса або косинуса. їх вивчення дає змогу досліджувати й складніші коливання, оскільки останні в багатьох випадках можна вважати такими, що складаються з певної кількості простих гармонічних коливань.

ГАРМОНІЧНІ КОЛИВАННЯ ТЯГАРЯ НА ПРУЖИНІ

Розглянемо рух тягаря, прикріпленого до пружини. Тягар має отвір, у який вставлено горизонтально розміщений стержень (мал. 2.1, 2.2).

Для спрощення розглянемо ідеальний випадок, коли тертя відсутнє, тобто немає втрат механічної енергії. Пізніше з'ясуємо вплив тертя на характер руху тягаря.

Коли на тягар у горизонтальному напрямку не діють зовнішні сили, то він перебуває у стані рівноваги (див. мал. 2.1, а). Сила тяжіння, яка діє на тягар, зрівноважується дією сили реакції стержня. Ці сили на рух тягаря не впливають.

Будемо відлічувати зміщення тягаря від положення рівноваги ОО'. Коли тягар перебуває справа від положення рівноваги, зміщення х вважатимемо додатними, а коли зліва — від'ємними.

Щоб тягар почав рухатися, його необхідно вивести зі стану рівноваги (див. мал. 2.1, б). При цьому, відповідно до закону Гука, виникне сила пружності, яка діє на тягар і напрямлена до положення рівноваги. З цього моменту й починаємо розгляд руху.
Якщо тягар відпустити, то під дією сили пружності пружини він почне рухатись до положення рівноваги, при цьому швидкість його руху зростатиме. В момент проходження тягарем через положення рівноваги його швидкість буде максимальною, а прискорення дорівнюватиме нулю (мал. 2.2, а).

Рухаючись далі, тягар стискує пружину, в ній виникає сила пружності, спрямована до положення рівноваги. Дійшовши до крайнього лівого положення, тягар буде рухатися до положення рівноваги (мал. 2.2, б).

Якщо розглядати ідеальний випадок, коли немає втрат механічної енергії, то рухи справа вліво і зліва вправо періодично повторюватимуться нескінченно довго. Саме періодичність і є найхарактернішою особливістю коливальних рухів.

Періодичність є найхарактернішою особливістю коливальних рухів

Проаналізуємо коливання тягаря під дією пружини. Коли тягар масою т зміщений від положення рівноваги на х (у положенні рівноваги х = 0), то на нього діє сила F = - kx, деk — жорсткість пружини (знак «—» означає, що сила у будь-який момент часу напрямлена в бік, протилежний зміщенню). За другим законом динаміки Ньютона F = та. Тому рівняння, яке описує рух тягаря, матиме такий вигляд:                           

або

У цьому рівнянні величина  завжди додатна, оскільки жорсткість пружини і маса тягаря не можуть набувати від'ємних значень. Відомо, що будь-яке число в квадраті  є додатним. Тому величину можна позначити як w ²  ,тоді рівняння руху тягаря буде таким:

Коли ви згодом вивчатимете основи диференціального й інтегрального числення, то зможете знайти розв'язок одержаного рівняння, а тут наведемо його в остаточному вигляді:

де x_max  і а — сталі   величини,  які  можна знайти з початкових умов руху.

Величину (wt + а) називають фазою коливанння а величину а — початковою фазою.

Розв'язок рівняння може бути и таким:      

але в цьому разі іншою буде початкова фаза а.

Величину (wt+ а) називають фазою коливання, а величину a  — початковою фазою

Останні два рівняння називають рівняннями гармонічного коливального руху.

Впевнитись у тому, що коливання відбуваються за законом косинуса чи синуса, можна й на досліді. До тягаря (див. мал. 2.1, 2-2) слід прикріпити перо з чорнилом або фарбою, вивести тягар із положення рівноваги і відпустити. Водночас у перпендикулярному до коливань напрямку рівномірно рухатимемо під тягарем чистий аркуш паперу, на якому одержимо графічне зображення гармонічних коливань (мал. 2.3). Такий характер можуть мати й електромагнітні коливання, про що ви дізнаєтеся з подальшого вивчення фізики.

Якщо здійснювати коливання з початковою фазою, що дорівнює нулю (а = 0), то легко встановити фізичну сутність величин x_max  і w. У цьому разі х = x_maxcoswt і в початковий момент руху t = 0, x = x_max (мал. 2.4, положення тягаря у точці 1). Це максимальне зміщення тягаря від положення рівноваги, яке називають амплітудою коливання.

Проаналізуємо рух тягаря, відпущеного у точці 1 (мал. 2.4).

, тіло перебуває у положенні рівноваги (точка 2). Якщо (wt = п, то х= -х_mах х = 0, тіло перебуває у точці 4. За wt = 2п  х = х_maх, тобто тіло повертається у вихідне положення, здійснивши одне повне коливання. За одне повне коливання тіло проходить усі точки траєкторії (крім крайніх) двічі — спочатку в одному напрямку, а потім у протилежному.

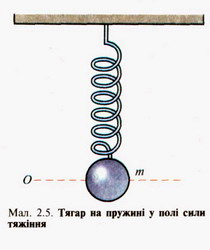
Інтервал часу, протягом якого тіло здійснює одне повне коливання, називають періодом коливання Т.

Максимальне зміщення тягаря від положення рівноваги називають амплітудою коливання

За одне повне коливання тіло проходить усі точки траєкторії (крім крайніх) двічі — спочатку в одному напрямку, а потім у протилежному

Інтервал часу, протягом якого тіло здійснює одне повне коливання, називають періодом коливання Т

Для розглянутого прикладу

,

звідки

Отже, величина w показує, яку кількість коливань здійснює тіло за 2п секунд. Цю величину називають коловою, або циклічною, частотою.

У процесі дослідження коливань користуються поняттям частоти f Частота коливань f показує, яку кількість коливань тіло здійснює за одну секунду. Легко помітити, що w = 2пf а . За міжнародною системою період визначають у секундах, а частоту — в одиницях за секунду. Ця одиниця названа герцом (Гц) на честь німецького фізика Генріха Герца, котрий у 1884 р. експериментально довів наявність електромагнітних хвиль.

Тепер можемо одержати формулу для визначення періоду коливань тягаря на пружині (див. мал. 2.1, 2.2). Якщо , то
, а період коливань , тоді частота коливань _.

За такими самими формулами визначають величини, які описують коливання тягаря на пружині, що підвішена вертикально (мал. 2.5).

У цьому разі сила тяжіння, що діє на тягар, зміщує лише положення рівноваги, а на характер коливань не впливає.
Коли тіло здійснює коливання, то періодично змінюються не лише його зміщення, а й швидкість та прискорення. У точках максимального відхилення від положення рівноваги (х = x_max і х = -х_mах) швидкість руху тіла дорівнює нулю, а прискорення максимальне, оскільки на тіло діє максимальна сила. Під час проходження тілом положення рівноваги  швидкість максимальна,  а  прискорення дорівнює нулю, бо сила, що діє на тіло, дорівнює нулю. Координата, швидкість та прискорення під час коливання змінюються з однаковим періодом Т.

Величина w показує, яку кількість коливань здійснює тіло за 2п секунд. Цю величину називають коловою, або циклічною, частотою

Частота коливань f показує, яку кількість коливань тіло здійснює за одну секунду

Коли тіло здійснює коливання, то періодично змінюються не лише його зміщення, а й швидкість та прискорення

ЕНЕРГІЯ КОЛИВАЛЬНОГО РУХУ

У механіці розрізняють кінетичну та потенціальну енергії тіл. Кінетична енергія визначається масою тіл та швидкістю їх руху:

Потенціальну енергію тіла у полі сил тяжіння визначають за формулою Е_п = mgh, а потенціальну енергію пружно деформованого тіла (наприклад, пружини)

Якщо розглядати рух тягаря, прикріпленого до пружини (див. мал. 2.1, 2.2), то тут періодично змінюватимуться як швидкість руху тіла, так і сила пружності пружини. Отже, періодично будуть змінюватися кінетична й потенціальна енергії. Кінетична енергія матиме максимальні значення у моменти проходження тілом положень рівноваги, а потенціальна — у моменти перебування тіла в точках найбільших відхилень від положення рівноваги.

Досі ми вважали, що в коливальних системах втрат механічної енергії немає, тому повна механічна енергія системи залишалася сталою:

Кінетична енергія матиме максимальні значення у моменти проходження тілом положень рівноваги, а потенціальна— у моменти перебування тіла в точках найбільших відхилень від положення рівноваги

У разі максимального відхилення тіла від положення рівноваги повна механічна енергія системи дорівнюватиме максимальній потенціальній енергії пружно деформованої пружини:

Оскільки  втратами  механічної енергії у системі ми поки що нехтуємо, то

Якщо не враховувати втрати механічної енергії у системі, то

З останнього рівняння можна легко знайти максимальне значення швидкості руху тіла в коливальному процесі. Зробіть це самі.

ВІЛЬНІ КОЛИВАННЯ

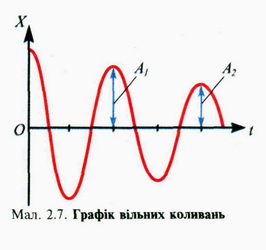
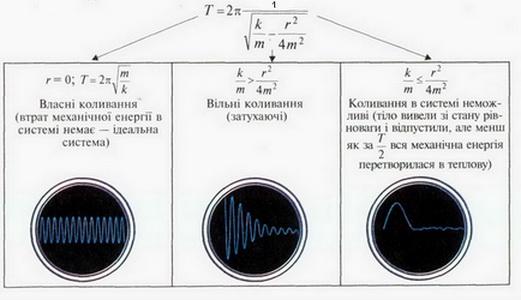
У попередніх розглянутих випадках коливань ми нехтували втратами механічної енергії у коливальних системах, тобто розглядали ідеальні випадки. Проте в реальних системах втрати механічної енергії завжди існують. Вони викликані наявністю тертя, опору середовища, утворенням механічних хвиль тощо. Тому амплітуда коливань у реальних системах з часом зменшується і коливання, зрештою, припиняються. Наприклад, з часом припиняються коливання тягаря на пружині чи гойдалки, якщо їх час від часу не підштовхувати, поповнюючи втрати механічної енергії. Якщо в коливальній системі тіло вивести зі стану рівноваги і відпустити, то воно здійснюватиме так звані вільні коливання, які завжди є затухаючими.

Для дослідження коливань різної природи часто використовують прилади, що дістали назву осцилографів. Осцилограф (від лат. oscillo — коливаюсь і грец. графо — пишу) — прилад для спостереження коливань та запису їх у графічній формі.

На мал. 2.7 зображено осцилограму вільних коливань.

Візьміть лінійку з міліметровими поділками і дослідіть за осцилограмою, чи залежить період таких коливань від їхньої амплітуди — виміряйте у міліметрах періоди коливань на початку осцилограми, в її середній частині та в кінці. Зробіть висновок.

Вочевидь, ви впевнились у тому, що період коливань від їхньої амплітуди не залежить.

Амплітуда коливань у реальних системах з часом зменшується і коливання, зрештою, припиняються

Вільні коливання завжди є затухаючими

Період коливань не залежить від їхньої амплітуди

У реальних механічних системах завжди є втрати механічної енергії

Досліджуючи коливання в системі тягар — пружина, за відсутності втрат механічної енергії, ми дійшли висновку, що період таких коливань можна визначити за формулою

А що ж ми маємо для вільних коливань? Вивчаючи фізику далі, ви переконаєтесь, що для вільних коливань ця формула набирає дещо іншого вигляду:

де  г — коефіцієнт опору,  що  характеризує втрати механічної енергії у системі.

Цю формулу можна й не запам'ятовувати, але проаналізувати її варто. Зрозуміло, що до неї входять величини, які мають лише додатні значення. Опір середовища збільшує період коливань тіла.

Період коливань має значення тільки більше за нуль. Це можливо лише за умови, що для підкореневого виразу забезпечується
умова . Якщо , то коливання в системі взагалі неможливі. Якщо ж коефіцієнт опору r = 0 (коливання відбуваються в ідеальній системі, без втрат механічної енергії), то

а це є період для гармонічних коливань тягаря на пружині. Такі коливання називають власними.

Викладені міркування зручно подати у такому вигляді:

Період власних коливань тягаря на пружині

Власними називають коливання в ідеальних системах

Висновки з цього легко перевірити експериментально. Якщо тягар, підвішений до пружини, вивести зі стану рівноваги і відпустити, то він коливатиметься досить довго. У воді його коливання відбуватимуться менш тривалий час, а у в'язкій рідині їх може не бути зовсім.

На практиці для визначення періоду вільних коливань користуються формулами для власних коливань, наприклад . Це цілком припустимо, оскільки похибки визначень у такому разі незначні.

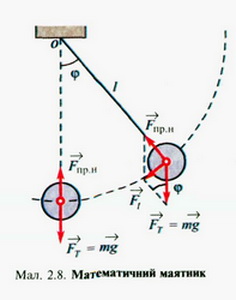
МАТЕМАТИЧНИЙ МАЯТНИК

Математичним маятником вважають точкове тіло, підвішене до нерозтяжної і невагомої нитки. Математичний маятник — це поняття абстрактне, тому що: по-перше, у природі не існує точкових тіл, а по-друге, немає абсолютно нерозтяжних і невагомих ниток.

Проте з певним наближенням математичним маятником можна вважати кульку, підвішену на нитці (мал. 2.8).

Коли кулька перебуває в стані рівноваги, то на неї діють сила тяжіння  та сила пружності нитки  які зрівноважують одна одну, тобто рівнодійна цих сил дорівнює нулю.

Якщо ж маятник відхилити від положення рівноваги на кут ер, то на кульку так само діятимуть сили тяжіння та пружності нитки, але їх рівнодійна  тепер уже має певне значення, напрямлена перпендикулярно до нитки маятника і діє у напрямку до положення рівноваги. Саме ця сила і викликає коливання маятника.

Якщо кут ф малий, то sinф ~ ф і сила, що викликає коливання, пропорційна куту відхилення нитки:

Такий самий характер має сила, що спричиняла коливання кульки, прикріпленої до пружини, яку розглядали вище.

Ця сила діє по дотичній до траєкторії руху кульки маятника і надає їй так званого тангенціального прискорення:

де / — довжина маятника (сумарна довжина нитки маятника і радіуса кульки); є — кутове прискорення руху маятника.

За другим законом Ньютона

Останнє рівняння аналогічне рівнянню
         к
а = - — х,  що описує  коливання тягаря  на пружині.
        m

Розв'язки обох рівнянь однакові. Якщо позначити  то колова частота коливань математичного маятника 

Оскільки період коливань  то період коливань математичного маятника буде

де / — довжина маятника; g — прискорення вільного падіння у точці, де перебуває маятник.

Це формула Гюйгенса для періоду коливань математичного маятника.

Загальною умовою виникнення механічних коливань є пропорційність прискорення руху тіл зміщеню, взятому зі знаком мініс:

У випадку криволінійного руху прискорення можна розділити на доцентрове, яке характеризує швидкість зміни напрямку швидкості, та тангенціальне, що характеризує швидкість зміни швидкості за значенням. Кутове прискорення

характеризує швидкість зміни кута повороту тіла при обертовому русі чи коливаннях навколо певних осей

Період коливань математичного маятника

Формула Гюйгенса для періоду коливань математичного маятника:

За допомогою маятників можна знаходити корисні копалини

З теоретичних міркувань, викладених у цьому параграфі, можна дійти таких висновків:
1.  Період коливань математичного маятника за малих амплітуд не залежить від амплітуди коливань. Ця властивість була відкрита Г. Галілеєм у 1583 р. і названа ізохронністю (рівночасністю).
2.  Період коливань не залежить від маси маятника.
3.  Період коливань прямо пропорційний квадратному кореню з довжини маятника.
4.  Період коливань обернено пропорційний квадратному кореню з прискорення вільного падіння.

Відомо, що в різних місцях земної кулі прискорення вільного падіння різне. Воно залежить не лише від форми Землі, а й від наявності під поверхнею важчих (руди різних металів ) чи легших (газ, нафта) речовин. Тому й період коливань маятника у таких місцях різний. Отже, за допомогою маятників можна знаходити корисні копалини, тобто допомагати геологічній розвідці.

ЗАПИТАННЯ
1. Наведіть приклади коливань. Які з них є механічними?
2. Що таке період, частота та колова, або циклічна, частота коливань? Як ці величини пов'язані між собою?
3. Яка основна одиниця вимірювання частоти? Що ви можете сказати про коливання тіл, які мають частоти коливань 0,5; 1,0 і 2,0 Гц?
4. Які величини, що характеризують коливальний рух, змінюються періодично?
5. Які властивості повинні мати сили, що викликають коливальний рух?
6. Які коливання вважають гармонічними?
7. В яких точках траєкторії тіло, що коливається, має лише потенціальну енергію?
8. В які моменти руху тіло, що коливається, має лише кінетичну енергію?
9. Як визначають потенціальну енергію тіла, що коливається? Яке максимальне значення може мати ця енергія?
10. Яке максимальне значення кінетичної енергії може мати тіло, що коливається? Яке у цьому разі значення швидкості тіла?
11. Яку повну механічну енергію має тіло, що коливається, у будь-якій точці траєкторії?
12. Чому в реальних системах відбуваються втрати механічної енергії?
13. За яких умов коливання не припинялися б взагалі?
14. За яких умов спостерігаються вільні коливання? Який характер має їхній графік?
15. За яких умов коливання зовсім неможливі?
16. Чи існують у природі власні коливання?
17. Які сили діють на кульку, підвішену на нитці, під час її коливання? Як ці сили змінюються?
18. Якими мають бути кулька та нитка, щоб маятник можна було вважати математичним?
19. Які умови потрібно забезпечити, щоб коливання були гармонічними?
20. Як зміниться період коливань маятника, якщо масу кульки збільшити (зменшити)?
21. Якою має бути амплітуда коливань маятника, розглянутого в цьому параграфі?

Є.В. Коршак, О.І. Ляшенко, В.Ф. Савченко, Фізика, 11 клас
Вислано читачами з інтернет-сайтів  

_{Повний перелік тем з фізики, календарний план по всім предметам згідно шкільної програми, домашня робота, курсита завдання з фізики для 11 класу}

Зміст уроку
 конспект уроку і опорний каркас                      
 презентація уроку 
 акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями)
 оцінювання 

Практика
 задачі та вправи,самоперевірка 
 практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання 

Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати
 фішки для допитливих
 шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати

Доповнення
 зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні 
 тематичні свята, девізи 
 статті 
 національні особливості
 словник термінів                          
 інше 

Тільки для вчителів
 ідеальні уроки 
 календарний план на рік 
 методичні рекомендації 
 програми
 обговорення

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.