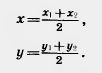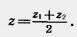Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Координаты середины отрезка(10 класс)

Координаты середины отрезка

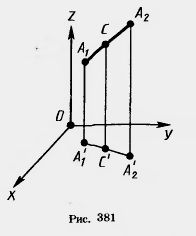
Пусть A₁ (x₁; у₁; z₁) и A₂ (x₂; у₂; z₂) — две произвольные точки. Выразим координаты х, у, z середины С отрезка А₁А₂ через координаты его концов А₁ и А₂ (рис. 381). Для этого проведем через точки А₁, А₂ и С прямые, параллельные оси z. Они пересекут плоскость ху в точках А^/₁(x₁; y₁; 0), А^/₂ ( x₂; y₂; 0) и С^/ (х; у; 0). По теореме Фалеса точка С^/ является серединой отрезока А₁, А₂.
 

А мы знаем, что на плоскости ху координаты середины отрезка выражаются через координаты его концов по формулам

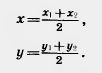
Для того чтобы найти выражение для z, достаточно вместо плоскости ху взять плоскость xz или yz. При этом для z получается аналогичная формула:

 
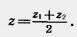
Задача (9). Докажите, что четырехугольник ABCD с вершинами в точках А (1; 3; 2), В (0; 2; 4), С(1; 1; 4), D (2; 2; 2) является параллелограммом.

Решение. Как мы знаем, четырехугольник, у которого диагонали пересекаются и точкой пересечения делятся пополам, есть параллелограмм. Воспользуемся этим для решения задачи. Координатами середины отрезка АС будут Мы видим, что координаты середин отрезков АС и BD одинаковы.

Значит, эти отрезки пересекаются и точкой пересечения делятся пополам. Следовательно, четырехугольник ABCD — параллелограмм.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.