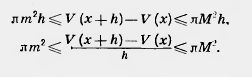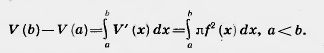Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Общая формула для объемов тел вращения

Общая формула для объемов тел вращения

Телом вращения в простейшем случае называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой. Круговой цилиндр, конус, шар являются примерами тел вращения. Найдем формулу для вычисления объема тела вращения.

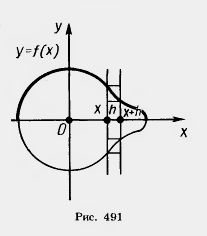
Проведем плоскость через ось тела и введем в этой плоскости декартовы координаты х, у, приняв ось тела за ось x (рис. 491). Плоскость ху пересекает поверхность тела по линии, для которой ось X является осью симметрии. Пусть y = f(x) — уравнение той части этой линии, которая расположена над осью х.

Проведем через точку (х,. О) плоскость, перпендикулярную оси х, и обозначим через V (х) объем части тела, лежащей слева от этой плоскости; V (х) является функцией от х.

Разность V {x + h) - V (х) представляет собой объем слоя тела толщиной h, заключенного между двумя плоскостями, которые перпендикулярны оси X и проходят через точки с абсциссами х и x + h.

Пусть М — наибольшее, а m —наименьшее значение функции f (х) на отрезке (х, x + h). Тогда рассматриваемый слой тела содержит  цилиндр с радиусом m и высотой h и содержится в цилиндре с радиусом М и той же высотой h (см. рис. 491). Поэтому

При стремлении высоты h к нулю левая и правая части последнего неравенства стремятся к одной и той же величине . Средняя же часть этого неравенства при стремлении h к О стремится к производной V'(x) функции V (х). Значит,
V'(x) = .

По известной формуле анализа

Эта формула и дает объем части тела, заключенной между параллельными плоскостями х = а и х = b.
 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.