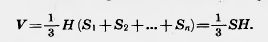|
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Объем пирамиды
Объем пирамиды
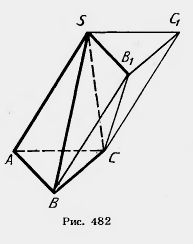
Пусть SABC — треугольная пирамида с вершиной S и основанием AВС. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой (рис. 482). Эта призма составлена из трех пирамид: данной пирамиды SABC и еще двух треугольных пирамид SCC1B1 и SCBB1.
У второй и третьей пирамид равные основания—  СС1В1 и СС1В1 и  В1ВС и общая высота, проведенная из вершины S. Поэтому у них равные объемы. В1ВС и общая высота, проведенная из вершины S. Поэтому у них равные объемы.
У первой и третьей пирамид тоже равные основания —  SAB и SAB и  BB1S и совпадающие высоты, проведенные из вершины С. Поэтому у них тоже равные объемы. BB1S и совпадающие высоты, проведенные из вершины С. Поэтому у них тоже равные объемы.
Значит, все три пирамиды имеют один и тот же объем. Так как сумма этих объемов равна объему призмы, то объемы пирамид равны-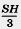
Итак, объем любой треугольной пирамиды, равен одной трети произведения площади основания на высоту:

Пусть теперь имеем любую, не обязательно треугольную пирамиду. Разобьем ее основание на треугольники  1, 1,  2. ... 2. ... n. Пирамиды, у которых основаниями являются эти треугольники, а вершинами — вершина данной пирамиды, составляют данную пирамиду. Объем данной пирамиды равен сумме объемов составляющих ее пирамид. Так как все они имеют ту же высоту Н, что и данная пирамида, то объем ее равен: n. Пирамиды, у которых основаниями являются эти треугольники, а вершинами — вершина данной пирамиды, составляют данную пирамиду. Объем данной пирамиды равен сумме объемов составляющих ее пирамид. Так как все они имеют ту же высоту Н, что и данная пирамида, то объем ее равен:
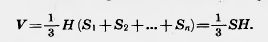
Итак, объем любой пирамиды равен одной трети произведения площади ее основания на высоту.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|