|
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Параллельные прямые в пространстве
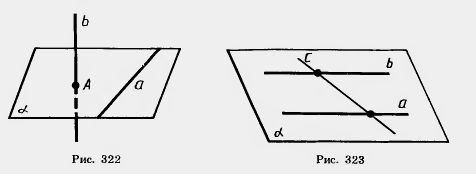
Решение. Так как данные прямые а и b параллельны, то через них можно провести плоскость (рис. 323). Обозначим ее Теорема 16.1. Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну. Замечание. Утверждение единственности в теореме 16.1 не является простым следствием аксиомы параллельных, так как этой аксиомой утверждается единственность прямой, параллельной данной в данной плоскости. Поэтому она требует доказательства.
Доказательство. Пусть a — данная прямая и А —точка, не лежащая на этой прямой (рис. 324). Проведем через прямую а и точку А плоскость Допустим, что существует другая прямая а2, проходящая через точку А и параллельная прямой a. Через прямые a и а2 можно провести плоскость
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: