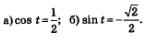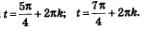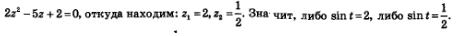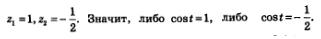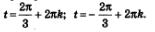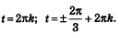|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Первые представления о решении тригонометрических уравнений
§16. Первые представления о решении тригонометрических уравнений
В главе 1 мы научились решать некоторые тригонометрические уравнения вида 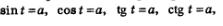 где а — действительное число. Например, мы знаем, что уравнения sin t = а и соs t =а не имеют решений, если а < -1 или а > 1, поскольку область значений функции s = sin t, равно как и функции s= соs t, есть отрезок [-1,1]. где а — действительное число. Например, мы знаем, что уравнения sin t = а и соs t =а не имеют решений, если а < -1 или а > 1, поскольку область значений функции s = sin t, равно как и функции s= соs t, есть отрезок [-1,1].
Напомним, как мы решали тригонометрические уравнения.
Пример 1. Решить уравнения: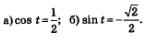
Решение: а) Используем геометрическую модель — числовую окружность на координатной плоскости (рис. 69). Отметим на окружности точки М и Р с абсциссой 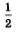 (они лежат на прямой (они лежат на прямой

В итоге получаем две серии решений уравнения:
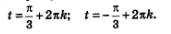
Обобщая, это можно записать так:
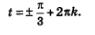
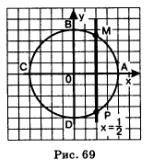
б) Используем геометрическую модель — числовую окружность на координатной плоскости (рис. 70). Отметим на окружности точки М и Р с ординатой -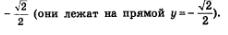 Точка М соответствует значению —, т.е. всем числам вида Точка М соответствует значению —, т.е. всем числам вида  Точка Р соответствует значению — Точка Р соответствует значению —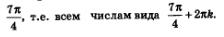
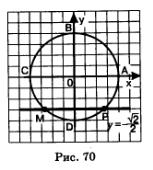
В итоге получаем две серии решений уравнения: 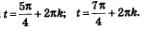
Решали мы и некоторые уравнения вида tg x =a, сtg х=а, используя для этого графики функций у = tg x, y = ctg x. Так, в § 15 мы, решив уравнение 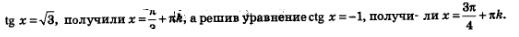
Впрочем, и уравнения вида sin х=а, соз х =а тоже можно решать графическим методом.
А как вы считаете, любое ли уравнение вида 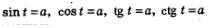 можно решить графически или с помощью числовой окружности? Для ответа на этот вопрос рассмотрим пример. можно решить графически или с помощью числовой окружности? Для ответа на этот вопрос рассмотрим пример.
Пример 2. Решить уравнения: 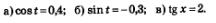
Решение: а) Нам нужно найти на числовой окружности точки с абсциссой 0,4 и записать, каким числам X они соответствуют. Абсциссу 0,4 имеют точки МиР (рис. 71), но каким числам X они соответствуют, мы не знаем. Решить это тригонометрическое уравнений мы пока не можем.
б) Нам нужно найти на числовой окружности точки с ординатой - 0,3 и записать, каким числам X они соответствуют. Ординату - 0,3 имеют точки ЬиИ (рис. 71), но каким числам X они соответствуют, мы не знаем. Решить это тригонометрическое уравнение мы тоже пока не можем.
в) Графики функций у = tg х и у = 2 имеют бесконечно много общих точек, абсциссы всех этих точек имеют вид 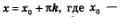 абсцисса точки пересечения прямой у =2 с главной ветвью тангенсоиды (рис. 72). Но что это за число х0, мы не знаем. Так что и тригонометрическое уравнение х = 2 мы пока решить не можем. абсцисса точки пересечения прямой у =2 с главной ветвью тангенсоиды (рис. 72). Но что это за число х0, мы не знаем. Так что и тригонометрическое уравнение х = 2 мы пока решить не можем.
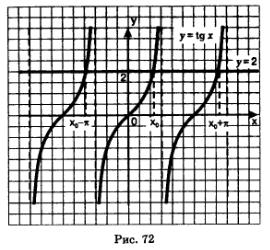
К уравнениям из примера 2 мы вернемся после того, как заложим необходимую теоретическую базу.
Итак, пока мы в состоянии решить тригонометрическое уравнение вида sin t =а, соs t =а только для конкретных значений а:
 эти уравнения не имеют решений. Уравнения вида tg=а, сtg х =а мы тоже в состоянии решить пока только для конкретных значений а: эти уравнения не имеют решений. Уравнения вида tg=а, сtg х =а мы тоже в состоянии решить пока только для конкретных значений а:
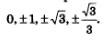
Но даже с помощью этого небольшого запаса знаний мы уже теперь можем решать некоторые более сложные уравнения.
Пример 3. Решить уравнение 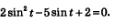
Решение. Введем новую переменную z = sin t. Тогда уравнение примет вид
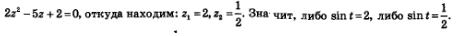
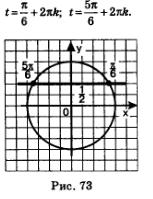
Первое из этих уравнений не имеет решений (вспомните почему), а для второго с помощью числовой окружности (рис. 73) находим две серии решений:
Пример 4. Решить уравнение 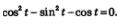
Решение. Воспользуемся тем, что 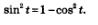 Тогда заданное Уравнение можно переписать в виде: Тогда заданное Уравнение можно переписать в виде:
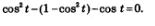
После понятных преобразований получим:
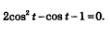
Введем новую переменную z =соs x. Тогда уравнение примет вид 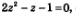 , откуда находим , откуда находим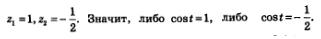 Первое из этих уравнений было решено в § 4 (см. пример 7): x= 2sin. Для второго уравнения с помощью числовой окружности (рис. 74) находим две серии решений: Первое из этих уравнений было решено в § 4 (см. пример 7): x= 2sin. Для второго уравнения с помощью числовой окружности (рис. 74) находим две серии решений:
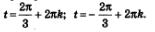
Ответ: 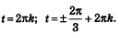
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|