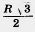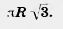|
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Пересечение двух сфер
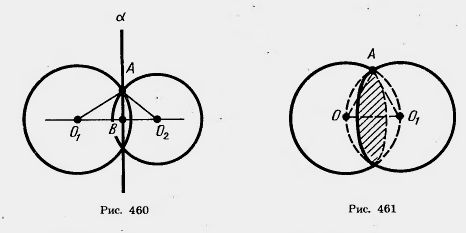
Доказательство. Пусть О1 и О2 — центры сфер и А — их точка пересечения (рис. 460). Проведем через точку А плоскость Обозначим через В точку пересечения плоскости Покажем теперь, что сферы не имеют других точек пересечения, кроме точек окружности К. Допустим, точка X пересечения сфер не лежит на окружности К. Проведем плоскость через точку X и прямую О1О2. Она пересечет сферы по окружностям с центрами О1 и О2. Эти окружности пересекаются в двух точках, принадлежащих окружности К, да еще в точке X. Но две окружности не могут иметь больше двух точек пересечения. Мы пришли к противоречию. Итак, пересечение наших сфер есть окружность (К). Теорема доказана. Задача (44). Два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найдите длину линии, по которой пересекаются их поверхности. Решение. Проведем сечение через центры шаров (рис. 461). Линия, о которой идет речь в задаче, есть окружность (теорема 20.6). Ее радиус равен высоте равностороннего треугольника ОАО1 со сторонами, равными R. Высота равна Следовательно, длина линии равна
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: