Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Перпендикулярность прямых в пространстве

Перпендикулярность прямых в пространстве

Так же как и на плоскости, две прямые называются перпендикулярными, если они пересекаются под прямым углом.

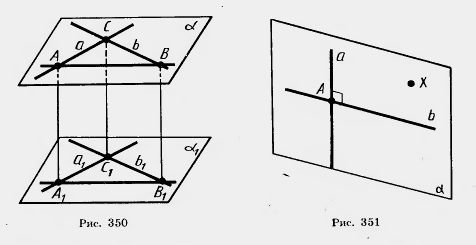
Теорема 17.1. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.

Доказательство. Пусть а и b — перпендикулярные прямые, а₁ и b₁ — параллельные им пересекающиеся прямые.

Докажем, что прямые а₁ и b₁перпендикулярны.

Если прямые а, b, а₁, b₁ лежат в одной плоскости, то они обладают указанным в теореме свойством, как это известно из планиметрии.

Допустим теперь, что наши прямые не лежат в одной плоскости. Тогда прямые а и b лежат в некоторой плоскости , а прямые а₁ и b₁ — в некоторой плоскости 1 (рис. 350). По теореме 16.4 плоскости и ₁ параллельны.. Пусть С — точка пересечения прямых а и b, а C₁ — точка пересечения прямых

а₁ и b₁. Проведем в плоскости параллельных прямых и ₁ прямую, параллельную прямой СС₁. Она пересечет прямые а и а₁ в точках А и А₁.B плоскости прямых b и b₁ проведем прямую, параллельную прямой СС₁, и обозначим через В и В₁ точки ее пересечения с прямыми b и b₁.

 
Четырехугольники САА₁С₁и СВВ₁С₁ — параллелограммы, так как у них противолежащие стороны параллельны. Четырехугольник АВВ₁ А₁ также параллелограмм. У него стороны АА₁, ВВ₁ параллельны, потому что каждая из них параллельна прямой CC₁. Таким образом, четырехугольник лежит в плоскости, проходящей через параллельные прямые АА₁ и ВВ₁. А она пересекает параллельные плоскости и ₁ по параллельным прямым АВ и А₁В₁.

Так как у параллелограмма противолежащие стороны равны, то АВ = А₁В₁, AC=А₁C₁, BC = B₁C₁. По третьему признаку равенства треугольников треугольники ABC и А₁В₁C₁ равны. Итак, угол А₁C₁B₁, равный углу АСВ, прямой, т. е. прямые а₁ и b₁ перпендикулярны. Теорема доказана.

Задача (1). Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.

Решение. Пусть a — прямая а А — точка на ней (рис. 351). Возьмем любую точку X вне прямой a и проведем через эту точку и прямую a плоскость (теорема 15.1). В плоскости через точку А можно провести прямую b, перпендикулярную прямой a.

 
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.