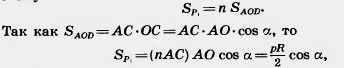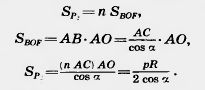Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Площадь круга

Площадь круга

Если фигура простая, т. е. допускает разбиение на конечное число треугольников, то ее площадь равна сумме площадей этих треугольников. Для произвольной фигуры площадь определяется следующим образом.

Данная фигура имеет площадь S, если существуют содержащие ее простые фигуры и содержащиеся в ней простые фигуры с площадями, как угодно мало отличающимися от S. Применим это определение к нахождению площади круга.

Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного. Эта точка называется центром круга, а данное расстояние — радиусом круга. Границей круга является окружность с теми же центром и радиусом (рис. 304).

Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

Докажем это. Построим два правильных n-угольника: Р₁ — вписанный в круг и Р₂ — описанный около круга (рис. 305). Многоугольники Р₁ и Р₂ являются простыми фигурами. Многоугольник Р₂ содержит круг, а многоугольник Р₁ содержится в круге.

Радиусы, проведенные в вершины многоугольника Р₁, разбивают его на n треугольников, равных треугольнику AOD. Поэтому

где р — периметр многоугольника Р₁, R — радиус круга. Аналогично находим площадь многоугольника Р₂:

 
Итак, многоугольник P₁, содержащийся в круге, имеет площадь

а многоугольник Р₂, содержащий круг, имеет площадь

Так как при достаточно большом n периметр р отличается сколь угодно мало от длины l окружности, а cos сколь угодно мало отличается от единицы, то площади многоугольников Р₁ и P₂ сколь угодно мало отличаются от . Согласно определению это значит, что площадь круга

что и требовалось доказать.

Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла (рис. 306).

Площадь кругового сектора вычисляется по формуле

где R — радиус круга, а — градусная мера соответствующего центрального угла.

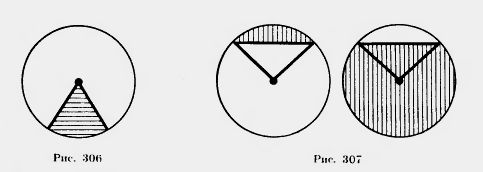
Круговым сегментом называется общая часть круга и полуплоскости (рис. 307).

Площадь сегмента, не равного полукругу, вычисляется по формуле

где — градусная мера центрального угла, который содержит дугу этого кругового сегмента, а S, — площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак « — » надо брать, когда < 180°, а знак «+» надо брать, когда > 180°.
 
 

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Библиотека с учебниками и книгами на скачку бесплатно онлайн, Математика для 9 класса скачать, школьная программа по математике, планы конспектов уроков}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.