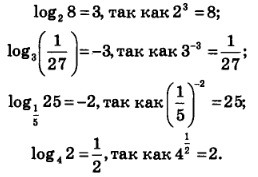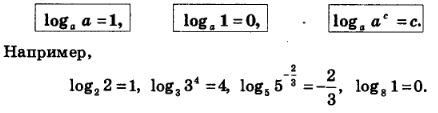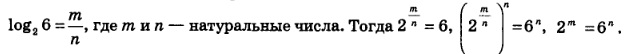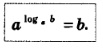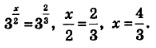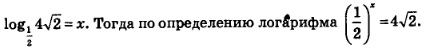|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Понятие логарифма
§ 48. Понятие логарифма
Рассмотрим уравнение 2х =4, решим его графически. Для этого в одной системе координат построим график функции у = 2 х и прямую у = 4(рис. 213). Они пересекаются в точкеА(2; 4), значит, х-2 — единственный корень уравнения.
Рассуждая точно так же, находим корень уравнения 2х =8 (см. рис. 213): х = 3.
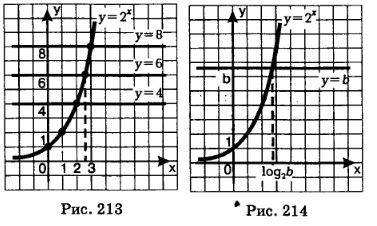
А теперь попробуем решить уравнение 2 х =6; геометрическая иллюстрация представлена на рис. 213. Ясно, что уравнение имеет один корень, но в отличие от предыдущих случаев, где корни уравнений были найдены без труда (причем их очень легко было найти и не пользуясь графиками), с уравнением 21 = 6 у нас возникают трудности: по чертежу мы не можем определить значение корня, можем только установить, что этот корень заключен в промежутке от 2 до 3.
С подобной ситуацией мы уже встречались в § 39, когда, решая уравнение х4 = 5, поняли, что надо вводить новый символ математического языка 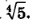 Обдумывая ситуацию с показательным уравнением 2х =6, математики ввели в рассмотрение новый символ log2, который назвали логарифмом по основанию 2 и с помощью этого символа корень уравнения 2х =6 записали так: х =log2 6 (читается: «логарифм числа 6 по основанию 2»). Теперь для любого уравнения вида 2х =Ь, где 6 >0, можно найти корень — им будет число log2 b (рис. 214). Обдумывая ситуацию с показательным уравнением 2х =6, математики ввели в рассмотрение новый символ log2, который назвали логарифмом по основанию 2 и с помощью этого символа корень уравнения 2х =6 записали так: х =log2 6 (читается: «логарифм числа 6 по основанию 2»). Теперь для любого уравнения вида 2х =Ь, где 6 >0, можно найти корень — им будет число log2 b (рис. 214).
Мы говорили об уравнении 2х =6. С равным успехом мы могли говорить и об уравнении 3x =5, и об уравнении 10x =0,3 и об уравнении 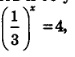 , и вообще о любом уравнении вида ax=b, где а и b — , и вообще о любом уравнении вида ax=b, где а и b —
положительные числа, причем аx 1. Единственный корень уравнения ах =Ъ математики договорились записывать так:
x=log5b (читается: «логарифм числа b по основанию а»).
Кстати, вернемся к уравнению 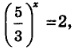 которое встретилось нам в примере 4 § 46 и которое мы не смогли решить. Теперь ответ ясен: которое встретилось нам в примере 4 § 46 и которое мы не смогли решить. Теперь ответ ясен: 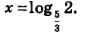
Определение. Логарифмом положительного числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
Например,
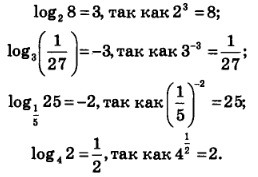
Особо выделим три формулы (попробуйте их обосновать, это очень просто):
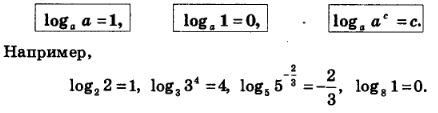
Для числа log2 6, которое встретилось нам в начале параграфа, точного рационального значения мы указать не можем, поскольку log2 6 — иррациональное число. Доказывается это довольно красиво.
Предположим, что log26 рациональное число, т.е. что 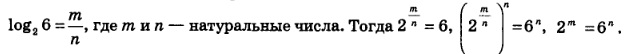
Последнее равенство невозможно, поскольку его правая часть есть целое число, которое делится без остатка на 3, а левая часть делиться без остатка на 3 никак не может.
Полученное противоречие означает, что наше предположение неверно и, следовательно, log2 6 — иррациональное число.
Мы дали определение логарифма на обычном языке, а теперь приведем то же определение на языке символов:
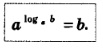
В самом деле, что надо подставить вместо x в равенство аx =b? Какое число должно находиться в показателе степени, в которую надо возвести число a, чтобы получить число b? Ответ следует из данного выше определения: этим показателем является logа b. Значит, вместо * надо подставить число logа b, что мы и сделали.
Например,
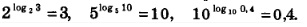
Подчеркнем, что logаЬ=с и ас =b — одна и та же математическая модель (одна и та же зависимость между числами а, b и с), но только вторая описана на более простом языке (использует более простые символы), чем первая.
Операцию нахождения логарифма числа обычно называют логарифмированием. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните:

Вычисление значения логарифма сводится, как правило, к решению некоторого показательного уравнения.
Пример.
Вычислить:
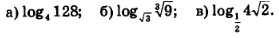
Решение. а) Положим: log4128 = x. Тогда по определению логарифма 4x =128. Решая это показательное уравнение, последовательно находим:
22x =27, 2х = 7, х=3,5.
б) Положим: 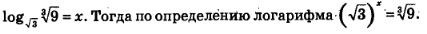 Решая это показательное уравнение, последовательно находим: Решая это показательное уравнение, последовательно находим:
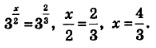
в) Положим:
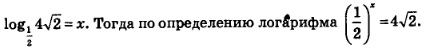
Решая это показательное уравнение, последовательно находим:
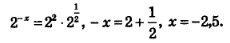
Логарифм по основанию 10 обычно называют десятичным логарифмом. Так, log10 5, log10 3,4 — десятичные логарифмы. Вместо символа log10 принято использовать символ так, вместо log10 5 пишут 5, а вместо log 10 3,4 пишут 3,4. В недалеком прошлом десятичным логарифмам отдавали предпочтение; опираясь на особенности принятой десятичной системы счисления, составляли весьма подробные таблицы десятичных логарифмов, наносили на шкалы специальных логарифмических линеек. В эпоху всеобщей компьютеризации десятичные логарифмы утратили свою ведущую роль, более важны стали логарифмы по основанию 2, но особенно широко используются в математике и технике логарифмы, основанием которых служит особое число е (такое же знаменитое, как число п); с этим числом мы познакомимся позднее (в § 54).
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|