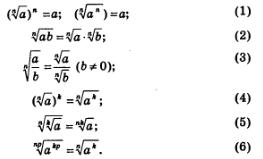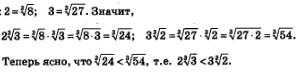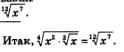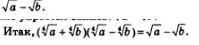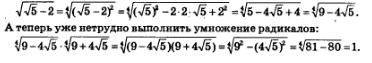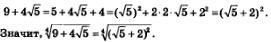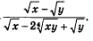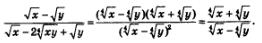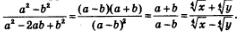Гипермаркет знаний>>Математика>>Математика 10 класс>> Преобразование выражений, содержащих радикалы

§ 42. Преобразование выражений, содержащих радикалы

В 7-м и 8-м классах вы выполняли преобразования рациональных выражений, используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т.д. В 8-м классе вы изучили новую операцию — операцию извлечения квадратного корня из неотрицательного числа и, используя свойства квадратных корней, выполняли преобразования выражений, содержащих квадратные корни. В предыдущих параграфах мы познакомились с операцией извлечения корня п-й степени из действительного числа, изучили свойства этой операции, а именно (для неотрицательных значений а и b):

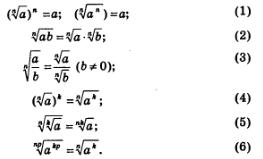
Используя эти формулы, можно осуществлять преобразования выражений, содержащих операцию извлечения корня (выражений с радикалами), — такие выражения называют иррациональными. Рассмотрим несколько примеров на преобразования иррациональных выражений.
Пример 1. Упростить выражения: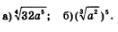

Решение: а) Представим подкоренное выражение 32а⁵ в виде 16- а⁴- 2а и воспользуемся формулой (2); получим: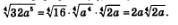
Полученное выражение считается более простым, чем заданное, поскольку под знаком корня содержится более простое выражение. Подобное преобразование называют вынесением множителя за знак радикала.
б) Воспользовавшись формулой (4), получим:

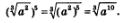
Представим подкоренное выражение а¹⁰ в виде а⁹ -а и воспользуемся формулой (2); получим:

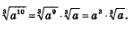
Как видите, и здесь удалось вынести множитель за знак радикала.

Вспомните формулу 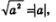которую вы изучали в курсе алгебры 8-го класса. Она обобщается на случай любого четного показателя корня
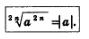
Эту формулу следует иметь в виду в тех случаях, когда нет уверенности в том, что переменные принимают только неотрицательные значения. Например, вынося множитель за знак корня в выражении 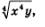, следует (если о знаке числа х ничего не известно) рассуждать так:

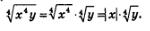
Наряду с вынесением множителя за знак радикала в необходимых случаях используется и преобразование, так сказать, противоположной направленности: внесение множителя под знак радикала. Это преобразование мы используем в следующих двух примерах.
Пример 2. Сравнить числа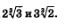
Решение. Имеем:

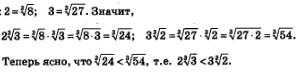
Пример 3. Упростить выражение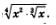
Решение. Сначала внесем множитель х¹ под знак корня 3-й степени:

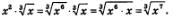
Теперь заданное выражение можно записать так: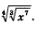
Воспользовавшись формулой (5), мы можем последнее выражение записать в виде

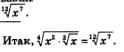
Пример 4. Выполнить действия:

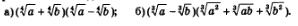
Решение: а) Здесь можно применить формулу сокращенного умножения «разность квадратов»:

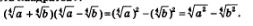
Воспользовавшись формулой (6), разделим в каждом из полученных радикалов показатели корня и подкоренного выражения на 2; это существенно упростит запись:

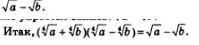
б) Здесь можно применить формулу сокращенного умножения «разность кубов»:

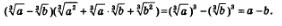
Пример 5. Выполнить действия:

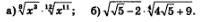
Решение: а) Поскольку перемножать можно корни только одной и той же степени, начнем с уравнивания показателей у имеющихся радикалов. Для этого дважды воспользуемся формулой (6):

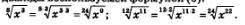
А теперь воспользуемся формулой (2):

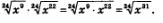
Осталось вынести множитель за знак радикала:

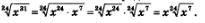
б) Первый способ. Преобразуем первый множитель в корень 4-й степени:

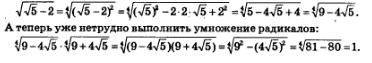
Второй способ. Сначала поработаем с подкоренным выражением во втором множителе. Имеем:

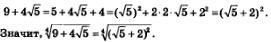
Разделив показатели корня и подкоренного выражения на 2, получим: 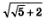(формулой (6) мы здесь имеем право пользоваться, поскольку подкоренное выражение 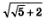— положительное число). Осталось выполнить умножение квадратных корней:

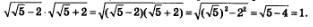
Пример 6. Разложить на множители: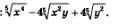

Решение. Заданное выражение можно переписать следующим образом: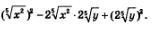
Теперь видно, что это — полный квадрат, квадрат разности выражений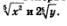
Окончательно получаем:

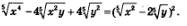
Пример 7. Сократить дробь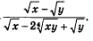
Решение. Первый способ. Знаменатель дроби можно преобразовать следующим образом:

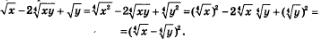
Значит, есть резон представить числитель как «разность квадратов»:

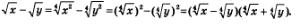
Далее, имеем:

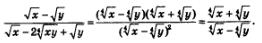
Второй способ. Введем новые переменные:

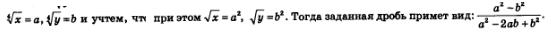
Что дала нам замена переменных? Она позволила заменить иррациональное выражение (с переменными х и у) рациональным выражением (с переменными а и b). А оперировать с рациональными выражениями намного проще, чем с иррациональными. Имеем:

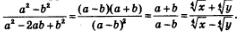
А.Г. Мордкович Алгебра 10 класс

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.