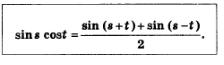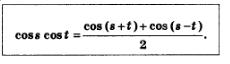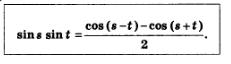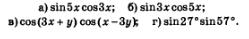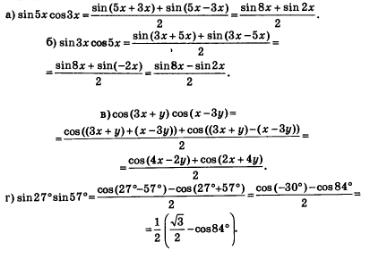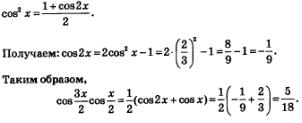|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Преобразование произведений тригонометрических функций в суммы
§ 27. Преобразование произведений тригонометрических функций в суммы
Сравните название этого параграфа с названием § 26, в котором речь шла о преобразование суммы (или разности) синусов или косинусов в произведение. Известно, что любая математическая формула на практике применяется как справа налево, так и слева направо. Поэтому неудивительно, что в тригонометрии приходится осуществлять и «движение в обратном направлении»: преобразовывать произведение тригонометрических функций в сумму. Об этом и пойдет речь в настоящем параграфе.
В § 26 мы видели, что sin(s + t)+ cos (s-t)=2sincost
Отсюда получаем:
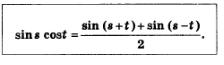
В § 26 мы видели, чтo сos(s + t) + сos(s-t) = 2coscost Отсюда получаем:
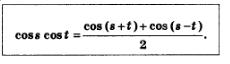
В § 26 мы видели, что соз (s-t)-соз (s-t) = -2sinssint Отсюда получаем:
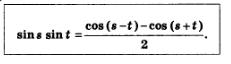
Таковы три формулы, позволяющие преобразовать произведение тригонометрических функций в сумму.
Пример 1. Преобразовать произведения в суммы: 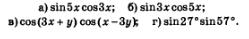
Решение.
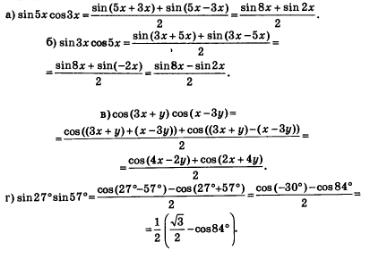
Пример 2. Найти значение выражения 
Решение. Имеем:

Значение соsх дано в условии, значение соз2х легко найти, воспользовавшись формулой понижения степени:
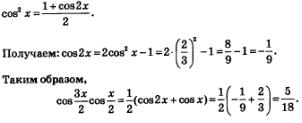
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|