|
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей
Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
На рисунке 365, а вы видите две перпендикулярные плоскости  и и  , пересекающиеся по прямой с. Плоскость , пересекающиеся по прямой с. Плоскость 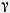 , перпендикулярная прямой с, пересекает плоскости , перпендикулярная прямой с, пересекает плоскости  и и  по перпендикулярным прямым а и b. по перпендикулярным прямым а и b.
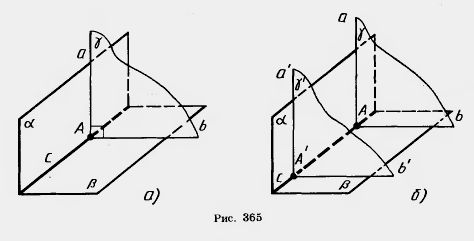
Любая плоскость, перпендикулярная линии пересечения перпендикулярных плоскостей, пересекает их по перпендикулярным прямым.
Действительно, если взять другую плоскость 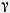 ', перпендикулярную прямой с (рис. 365, б), то она пересечет плоскость ', перпендикулярную прямой с (рис. 365, б), то она пересечет плоскость  по прямой а', перпендикулярной с, а значит, параллельной прямой а, а плоскость по прямой а', перпендикулярной с, а значит, параллельной прямой а, а плоскость  по прямой b', перпендикулярной с и, значит, параллельной прямой b. По теореме 17.1 из перпендикулярности прямых а и b следует перпендикулярность прямых а' и b', что и требовалось доказать. по прямой b', перпендикулярной с и, значит, параллельной прямой b. По теореме 17.1 из перпендикулярности прямых а и b следует перпендикулярность прямых а' и b', что и требовалось доказать.
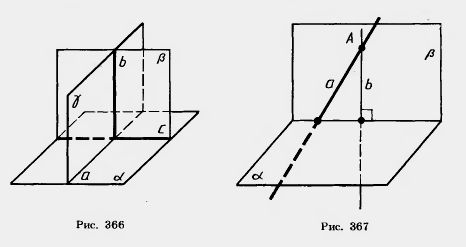
Теорема 17.6. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Доказательство. Пусть  — плоскость, b — перпендикулярная ей прямая, — плоскость, b — перпендикулярная ей прямая,  — плоскость, проходящая через прямую b и с — прямая, по которой пересекаются плоскости — плоскость, проходящая через прямую b и с — прямая, по которой пересекаются плоскости  и и  (рис. 366). Докажем, что плоскости (рис. 366). Докажем, что плоскости  и и  перпендикулярны. перпендикулярны.
Проведем в плоскости  через точку пересечения прямой b с плоскостью через точку пересечения прямой b с плоскостью  прямую а, перпендикулярную прямой с. Проведем через прямые а и b плоскость прямую а, перпендикулярную прямой с. Проведем через прямые а и b плоскость 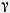 . Она перпендикулярна прямой с, так как прямая с перпендикулярна прямым а и b. Так как прямые а и b перпендикулярны, то плоскости . Она перпендикулярна прямой с, так как прямая с перпендикулярна прямым а и b. Так как прямые а и b перпендикулярны, то плоскости  и и  перпендикулярны. Теорема доказана. перпендикулярны. Теорема доказана.
Задача (54). Даны прямая а и плоскость  . Проведите через прямую а плоскость, перпендикулярную плоскости . Проведите через прямую а плоскость, перпендикулярную плоскости  . .
Решение. Через произвольную точку прямой а проводим прямую b (рис. 367), перпендикулярную плоскости  (задача 12). Через прямые a и b проводим плоскость (задача 12). Через прямые a и b проводим плоскость  . Плоскость . Плоскость  перпендикулярна плоскости перпендикулярна плоскости  по теореме 17.6. по теореме 17.6.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












