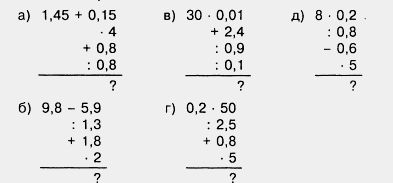Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика: Проценты

Проценты

Сотую часть центнера называют килограммом, сотую часть метра — сантиметром, сотую часть гектара — аром или соткой. Принято называть сотую часть любой величины или числапроцентом. Значит, 1 кг — один процент центнера, 1 см — один процент метра, 1 а — один процент гектара, 0,02 — один процент от 2.

Процентом называют одну сотую часть.

Для краткости слово «процент» после числа заменяют знаком %. Предложение «В поход ушли 1,5% учащихся нашей школы» читают так:

«В поход ушли полтора процента учащихся нашей школы», а предложение «В этом месяце заработная платавыросла на 8%» читают так: «В этом месяце заработная плата выросла на восемь процентов».

Так как 1% равен сотой части величины, то вся величина равна 100%.

Задача 1. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Решение. Так как 1200 костюмов — это 100% выпуска, то, чтобы найти 1% выпуска, надо 1200 разделить на 100. Получим, что 1200 : 100 = 12, значит, 1% выпуска равен 12 костюмам. Чтобы найти, чему равны 32% выпуска, надо умножить 12 на 32. Так как 12 • 32 = 384, то фабрика выпустила 384 костюма нового фасона.

Задача 2. За контрольную работу по математике отметку «5» получили 12 учеников, что составляет 30% всех учеников. Сколько учеников в классе?

Решение. Сначала узнаем, чему равен 1% всех учеников. Для этого разделим 12 на 30. Так как 12 : 30 = 0,4, то 1% равен 0,4. Чтобы узнать, чему равны 100% учащихся, надо умножить 0,4 на 100. Так как 0,4 • 100 = 40, то в классе 40 учеников.

Задача 3. Из 1800 га поля 558 га засажено картофелем. Какой процент поля засажен картофелем?
Решение. Картофелем засажено всего поля. Обратим дробь в десятичную. Для этого разделим 558 на 1800. Получаем 0,31. Значит, картофелем засажена 31 сотая всего поля. Каждая сотая равна 1% поля, поэтому картофелем засажен 31% всего поля.
Чтобы обратить десятичную дробь в проценты, надо ее умножить на 100.
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.
Например, 0,971 = 0,971 . 100% = 97,1%; 39% = 39 : 100 = 0,39.

Что называют процентом?
Как называют 1% от центнера, метра, гектара?
Как обратить десятичную дробь в проценты?
Как перевести проценты в десятичную дробь?

1561. Запишите в виде десятичной дроби:

1%; 6%; 45%; 123%; 2,5%; 0,4%.

1562. Запишите в процентах десятичные дроби:
0,87; 0,07; 1,45; 0,035; 2,672; 0,907.

1563. Запишите обыкновенные дроби в виде десятичных, а потом в виде процентов.
1564. Заполните таблицу:

1565. В школьной библиотеке 7000 книг. Маша прочитала одну сотую всех этих книг. Сколько библиотечных книг прочитала Маша? Сережа прочитал 1% всех книг школьной библиотеки. Сравните число библиотечных книг, прочитанных Машей и Сережей.

1566. В палатку завезли 850 кг огурцов. Первый покупатель взял для соления 1% всех огурцов, а второй — 3% всех огурцов. Сколько килограммов огурцов купил каждый из них?

1567. На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка убрали за сутки?

1568. Бригаде поручили отремонтировать участок дороги длиной 760 м. Сколько метров дороги бригада отремонтирует, когда выполнит: 30% задания; 50% задания; 10% задания?

1569. Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

1570. В плодовом саду собирали яблоки. За день было собрано 4840 кг. 25% собранных яблок отправили в магазин, а остальные — на склад. Сколько килограммов яблок отправили на склад?

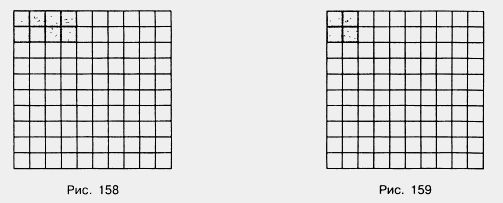
1571. Себестоимость изготовления одной детали равна 650 р. Внедрение новой технологии позволило снизить себестоимость детали на 2%. Какова стала себестоимость такой детали?

1572. Поле на рисунке 158 разбито на 100 долей. Закрашенная на рисунке часть засеяна горохом. Найдите площадь всего поля, если горохом засеяно 24,8 га.

1573. Сколько человек было в кино, если 1% всех зрителей составляет 7 человек?

1574. Мотоциклист за день проехал некоторое расстояние. 1% пути он ехал по проселочной дороге, что составило 3,2 км. Какое расстояние проехал мотоциклист за день?

1575. Двор разбит на 100 равных частей. Часть площади двора, закрашенная на рисунке 159, отведена под стоянку машин. Найдите площадь двора, если стоянка занимает 146,4 м².

1576. Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?

1577. Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.

1578. Сливочное мороженое содержит 14% сахара. На приготовление мороженого израсходовали 35 кг сахара. Сколько сделали порций мороженого, если в каждой порции 100 г?

1579. Применяя интенсивную технологию, бригада изготовила сверх плана 250 деталей, перевыполнив тем самым план на 5%. Сколько деталей изготовила бригада?

1580. В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?

1581. Фрекен Бок испекла 80 пирожков, и Карлсон тут же съел 10 пирожков. Сколько процентов всех пирожков съел Карлсон?

1582. В механическом цехе установлено 350 станков, из которых 35 находятся в ремонте. Сколько процентов станков находятся в действующем состоянии?

1583. При плане 35 деталей в день рабочий сделал 42 детали. На сколько процентов он выполнил норму? На сколько процентов он перевыполнил норму?

1584. Сколько процентов соли содержит раствор, приготовленный из 35 г соли и 165 г воды?

1585. В 4 А классе 40 учеников. С задачей справились 32 ученика. В 4 Б классе 35 учеников, а с задачей справились 28 учеников. Какой класс лучше справился с задачей?

1586. Найдите 0,3 числа:   

а) 150;           б) 600;         в) 100;          г) 5.

1587. Вычислите устно:

1588. Представьте в виде десятичной дроби числа 
1589. Восстановите цепочки вычислений и попробуйте объяснить, почему они приводят к одному ответу:

1590. Собственная скорость катера 18 км/ч. Отметьте ее на координатном луче. Вычислите и отметьте на этом луче скорости катера против течения и по течению, если скорость течения 1,5 км/ч. Используя чертеж, подумайте:

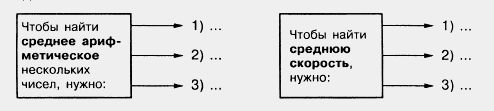
а) как найти собственную скорость катера, если известны его скорости по течению и против течения;
б) как найти скорость катера против течения, если известны скорость течения и скорость катера по течению;
в) на сколько скорость катера по течению больше его скорости против течения.

1591. Попробуйте представить правило нахождения среднего арифметического нескольких чисел и средней скорости в виде последовательности команд по схемам:

1592. Найдите значение выражения:

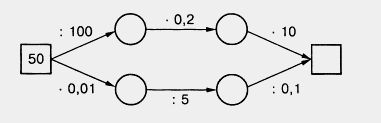
а) 2,0928 + 47,9072 : (7 - 0,195);
б) 100,5876 - 88,5856 : (6,0811 + 8,4889);
в) 687,8 + (88,0802 - 85,3712) : 0,045.
Проверьте ответ с помощью микрокалькулятора.

1593. Автобус шел 3 ч по шоссе, 1,5 ч по грунтовой дороге и 0,5 ч по проселочной дороге. Известно, что скорость автобуса по грунтовой дороге была в 2 раза больше скорости по проселочной дороге, а скорость по шоссе в 3,5 раза больше скорости по проселочной дороге. Найдите скорость движения автобуса по проселочной дороге, если средняя скорость автобуса на всем пути 33,6 км/ч.

1594. Марина сварила варенье, истратив имевшегося у нее сахара. Сколько сахара осталось у Марины, если на варенье она израсходовала 0,8 кг сахара?
1595. В куске было 112,2 м материи. В первый раз отрезали кyска а во второй раз куска. Сколько метров материи было отрезано за оба раза?

1596. Выполните действия:

1) (3,1 • 5,3 - 14,39) : 1,7 + 0,8;
2) (21,98 - 4,2 • 4,6) : 1,9 + 0,6.

1597. Решите задачу:

1) Первое число в 2,4 раза больше третьего, а второе число на 0,6 больше третьего числа. Найдите эти три числа, если их среднее арифметическое равно 2,4.

2) Второе число на 0,8 больше первого, а третье число в 3,2 раза больше первого. Найдите эти три числа, если их среднее арифметическое равно 4,6.

1598. Запишите в виде процентов десятичные дроби

6,51;         2,3;           0,095.

1599. Запишите в виде десятичной дроби

42%;          8%;           7,25%;          568%.

1600. Слесарь и его ученик изготовили 1200 деталей. Ученик сделал 30% всех деталей. Сколько деталей сделал ученик?

1601. На водопой пригнали 220 лошадей и жеребят. Жеребята составляли 15% всего табуна. Сколько жеребят было в табуне?

1602. Геологи проделали путь длиной 2450 км. 10% пути они пролетели на самолете, 60% пути проплыли в лодках, а остальную часть прошли пешком. Сколько километров геологи прошли пешком?

1603. Из молока получается 10% творога. Сколько творога получится из 32,8 кг молока? Из 58,7 кг молока?

1604. Площадь одной комнаты 12 м², и она составляет 25% площади всей квартиры. Найдите площадь всей квартиры.

1605. Автотурист проехал в первый день 120 км, что составляет 15% всего намеченного пути. Какой длины намеченный путь?

1606. Засеяли 24% поля. Осталось засеять 45,6 га этого поля. Найдите площадь всего поля.

1607. Из пшеницы получается 80% муки. Сколько смололи пшеницы, если получили 2,4 т муки? Сколько муки получится из 2,5 т пшеницы?

1608. Масса сушеных яблок составляет 16% массы свежих яблок. Сколько надо взять свежих яблок, чтобы получить 4 т сушеных? Сколько сушеных яблок получится из 4,5 т свежих яблок?

1609. Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?

1610. В классе 17 мальчиков, а девочек на 6 больше. Сколько процентов класса составляют девочки и сколько процентов класса составляют мальчики?

1611. В санатории отдыхали мужчины и женщины. Мужчины составляли 40% всех отдыхающих. Какой процент всех отдыхающих составляли женщины?

1612. Выполните действия:

а) (3,8 • 1,75 : 0,95 - 1,02) : 2,3 + 0,4;
б) (11,28 + 3,4 : 0,85 • 1,55) : 4,6 - 0,8.

Слово «процент» происходит от латинских слов pro centum, что буквально означает «со ста».

Проценты дают возможность легко сравнивать между собой части целого, упрощают расчеты и поэтому очень распространены.

Широко начали использовать проценты в Древнем Риме, но идея процентов возникла много раньше — вавилонские ростовщики уже умели находить проценты (но они считали не «со ста», а «с шестидесяти», так как в Вавилоне пользовались шестидесятеричными дробями).

Знак % произошел, как предполагают, благодаря опечатке. В рукописях pro centum часто заменяли словом «cento» (сто) и писали его сокращенно — cto. в 1685 году в Париже была напечатана книга — руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %.

После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.

Иногда применяют и более мелкие доли целого —тысячные, то есть десятые части процента. Их называют промилле (от латинского «с тысячи») и обозначают %0.

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Книги и учебники согласно календарному плануванння по математике 5 класса скачать, помощь школьнику онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.