Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми

Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.

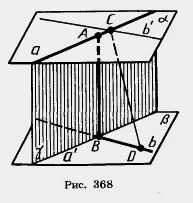
Докажем, что две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.

Действительно, пусть а и b — данные скрещивающиеся прямые (рис. 368).

Проведем через них параллельные плоскости и . Прямые, пересекающие прямую а и перпендикулярные плоскости , лежат в одной плоскости (). Эта плоскость пересекает плоскость по прямой а', параллельной а. Пусть В — точка пересечения прямых а' и b. Тогда прямая АВ, перпендикулярная плоскости , перпендикулярна и плоскости , так как параллельна . Отрезок АВ — общий перпендикуляр плоскостей и , а значит, и прямых а и b.

Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых а и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b', параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b'. Так как она перпендикулярна прямой а, то она перпендикулярна плоскости , а значит, параллельна прямой АВ. Выходит, что через прямые АВ и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые АС и BD, а это невозможно, что и требовалось доказать.

Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые.


А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.