Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Сечения цилиндра плоскостями

Сечения цилиндра плоскостями

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 435). Две его стороны — образующие цилиндра, а две другие — параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это — сечение цилиндра плоскостью, проходящей через его ось (рис. 436).

Задача (2). Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.

Решение. Сторона квадрата равна 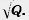. Она равна диаметру основания. Поэтому площадь основания равна.

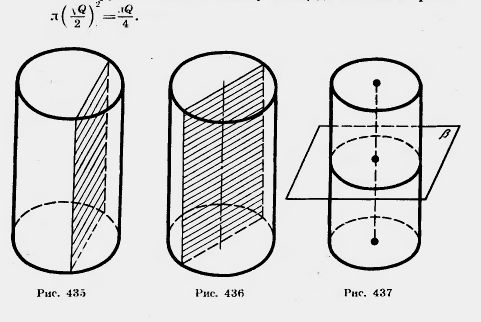
Теорема 20.1. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Доказательство. Пусть — плоскость, параллельная плоскости основания цилиндра (рис. 437). Параллельный перенос в направлении оси цилиндра, совмещающий плоскость с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью с окружностью основания. Теорема доказана.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.