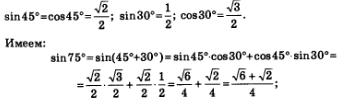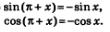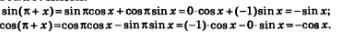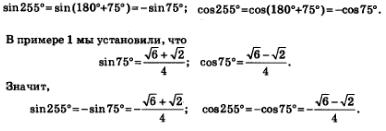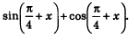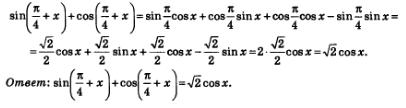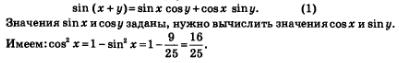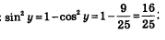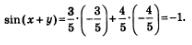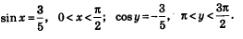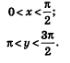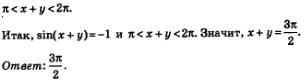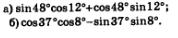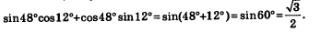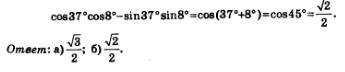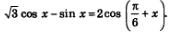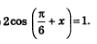|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Синус и косинус суммы аргументов
§21. Синус и косинус суммы аргументов
В этой главе речь пойдет о преобразовании тригонометрических выражений. Для этого используются различные -тригонометрические формулы, основные из которых мы внимательно рассмотрим.
Пожалуй, самыми важными в тригонометрии являются следующие две формулы (доказательства их технически довольно сложны, и мы их здесь не приводим):
Эти формулы обычно называют синус суммы и косинус суммы. А считаются они самыми важными потому, что, как мы увидим далее, из этих формул без особого труда выводятся практически все формулы тригонометрии. Поэтому есть смысл уделить указанным формулам особое внимание. Рассмотрим примеры, в которых используются формулы синуса суммы и косинуса суммы. Учтем при этом, что каждая из указанных формул применяется на практике как «слева направо», так и «справа налево».
Пример 1. Вычислить sin 75° и соs 75°.
Решение. Воспользуемся тем, что 75° — 45° + 30° , и тем, что значения синуса и косинуса от углов 45° и 30° мы знаем:
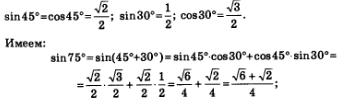
Пример 2. Доказать, что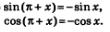 
Решение. Имеем:
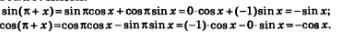
Замечание. Вернемся к доказанному в § 4 свойству 3. Это те самые тождества (формулы приведения), которые только что доказаны в примере 2, но ранее мы получили их с помощью числовой окружности, а сейчас — с помощью формул синуса и косинуса суммы.
Пример 3. Вычислить sin x и соs x, если х =255°.
Решение. Имеем:
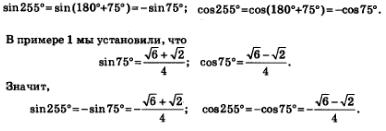
Пример 4. Упростить выражение
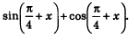
Решение. Имеем:
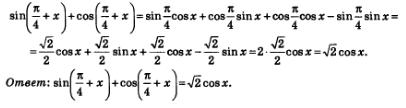
Пример 5. Вычислить sin (x + у), если известно, что
Решение. Воспользуемся формулой синуса суммы:
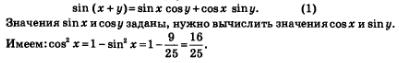
По условию аргумент х принадлежит первой четверти, а в ней косинус положителен. Поэтому из равенства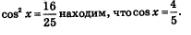 
Имеем: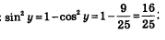 
По условию аргумент у принадлежит третьей четверти, а в ней синус отрицателен. Поэтому из равенства: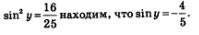 
Подставим заданные и найденные значения в правую часть формулы (1):
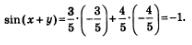
Ответ: -1.
Пример 6. Вычислить х + у, если известно, что
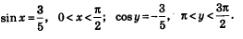
Решение. В предыдущем примере мы установили, что при заданных условиях sin (x+ у)=-1.
По условию данного примера, как и в примере 5,
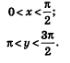
Сложив эти два двойных неравенства, получим:
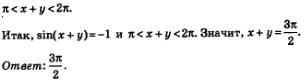
Пример 7. Вычислить:
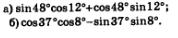
Решение, а) Заданное выражение можно «свернуть» в синус суммы аргументов 48° и 12°, получим:
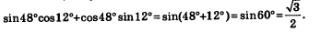
б) Заданное выражение можно «свернуть» в косинус суммы аргументов 37° и 8°, получим:
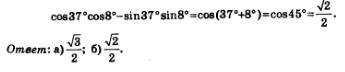
Пример 8. Упростить выражение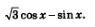 
Решение. Если переписать заданное выражение в виде
Пример 9. Решить уравнение: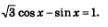 
Решение.В предыдущем примере мы получили, что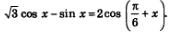 
Значит, заданное уравнение можно переписать в виде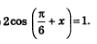 
Решая это уравнение, последовательно находим:
Итак, мы познакомились с двумя тригонометрическими формулами: «синус суммы» и «косинус суммы», увидели, как эти формулы используются для доказательства тригонометрических тождеств и упрощения тригонометрических выражений, для отыскания значений тригонометрических выражений и решения тригонометрических уравнений. В § 22 мы проделаем аналогичную работу с формулами «синус разности» и «косинус разности».
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
