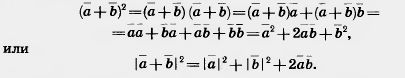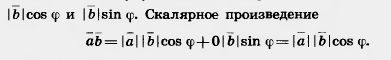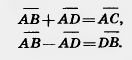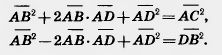|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Скалярное произведение векторов
Скалярное произведение векторов
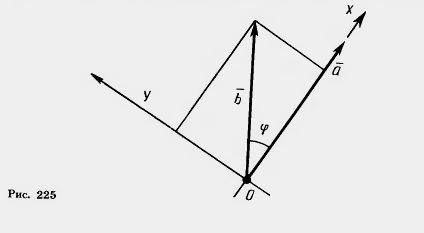
Для скалярного произведения векторов используется такая же запись, как и для произведения чисел. Скалярное произведение Из определения скалярного произведения векторов следует, что для любых векторов Действительно, левая часть равенства есть (а1;b1)c1 + (а2;b2)c2 , а правая a1c1 + a2 c2 + b1c1 + b2 c2 . Очевидно, они равны. Углом между ненулевыми векторами Теорема 10.3. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними. Доказательство. Пусть
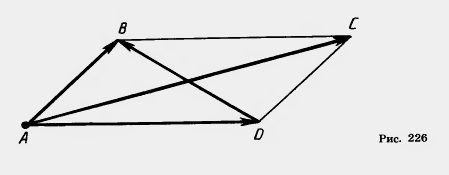
Из теоремы 10.3 следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны. Задача (38). Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Решение. Пусть четырехугольник ABCD — параллелограмм (рис. 226). Имеем векторные равенства
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планирование математике, материалы по математике 8 класса скачать, учебники онлайн
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: