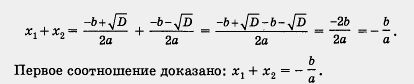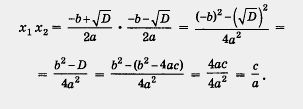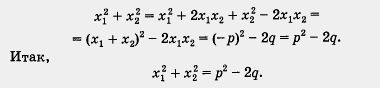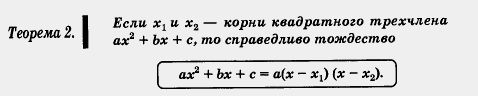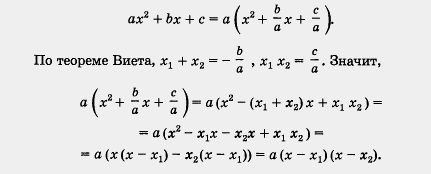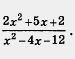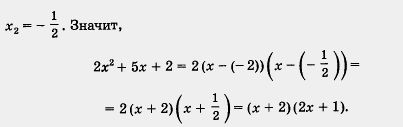|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Теорема Виета''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Теорема Виета''' |
| | | | |
| | + | <br> |
| | | | |
| | + | ''' ТЕОРЕМА ВИЕТА '''<br> |
| | | | |
| - | ''' ТЕОРЕМА ВИЕТА '''<br>
| + | <br>В этом параграфе мы познакомимся с любопытными соотношениями между корнями квадратного уравнения и его коэффициентами. Эти соотношения впервые обнаружил французский математик Франсуа Виет (1540—1603). |
| | | | |
| - | <br>В этом параграфе мы познакомимся с любопытными соотношениями между корнями квадратного уравнения и его коэффициентами. Эти соотношения впервые обнаружил французский математик Франсуа Виет (1540—1603).
| + | <br> |
| - | | + | |
| - | <br> | + | |
| | | | |
| | [[Image:14-06-47.jpg]]<br><br>Например, для уравнения Зx<sup>2</sup> - 8x - 6 = 0, не находя его корней, можно, воспользовавшись теоремой Виета, сразу сказать, что сумма корней равна [[Image:14-06-48.jpg]], а произведение корней равно [[Image:14-06-49.jpg]]<br> т. е. - 2. А для уравнения х<sup>2</sup> - 6х + 8 = 0 заключаем: сумма корней равна 6, произведение корней равно 8; между прочим, здесь нетрудно догадаться, чему равны корни: 4 и 2. <br>Доказательство теоремы Виета. Корни х<sub>1</sub> и х<sub>2</sub> квадратного уравнения ах<sup>2</sup> + bх + с = 0 находятся по формулам | | [[Image:14-06-47.jpg]]<br><br>Например, для уравнения Зx<sup>2</sup> - 8x - 6 = 0, не находя его корней, можно, воспользовавшись теоремой Виета, сразу сказать, что сумма корней равна [[Image:14-06-48.jpg]], а произведение корней равно [[Image:14-06-49.jpg]]<br> т. е. - 2. А для уравнения х<sup>2</sup> - 6х + 8 = 0 заключаем: сумма корней равна 6, произведение корней равно 8; между прочим, здесь нетрудно догадаться, чему равны корни: 4 и 2. <br>Доказательство теоремы Виета. Корни х<sub>1</sub> и х<sub>2</sub> квадратного уравнения ах<sup>2</sup> + bх + с = 0 находятся по формулам |
| Строка 23: |
Строка 23: |
| | [[Image:14-06-54.jpg]]<br><br>Однако основное назначение теоремы Виета не в том, что она выражает некоторые соотношения между корнями и коэффициентами квадратного уравнения. Гораздо важнее то, что с помощью теоремы Виета выводится формула разложения квадратного трехчлена на множители, без которой мы в дальнейшем не обойдемся. | | [[Image:14-06-54.jpg]]<br><br>Однако основное назначение теоремы Виета не в том, что она выражает некоторые соотношения между корнями и коэффициентами квадратного уравнения. Гораздо важнее то, что с помощью теоремы Виета выводится формула разложения квадратного трехчлена на множители, без которой мы в дальнейшем не обойдемся. |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | [[Image:14-06-55.jpg]]<br><br>Доказательство. Имеем | | [[Image:14-06-55.jpg]]<br><br>Доказательство. Имеем |
| | | | |
| - | [[Image:14-06-56.jpg]]<br>'''<br>Пример 1'''. Разложить на множители квадратный трехчлен Зх<sup>2</sup> - 10x + 3. <br>Решение. Решив уравнение Зх<sup>2</sup> - 10x + 3 = 0, найдем корни квадратного трехчлена Зх<sup>2</sup> - 10x + 3: х<sub>1</sub> = 3, х2 = [[Image:14-06-57.jpg]]. <br>Воспользовавшись теоремой 2, получим <br> | + | [[Image:14-06-56.jpg]]<br>'''<br>Пример 1'''. Разложить на множители квадратный трехчлен Зх<sup>2</sup> - 10x + 3. <br>Решение. Решив уравнение Зх<sup>2</sup> - 10x + 3 = 0, найдем корни квадратного трехчлена Зх<sup>2</sup> - 10x + 3: х<sub>1</sub> = 3, х2 = [[Image:14-06-57.jpg]]. <br>Воспользовавшись теоремой 2, получим <br> |
| | | | |
| - | [[Image:14-06-58.jpg]]<br><br>Есть смысл вместо [[Image:14-06-59.jpg]] написать Зx - 1. Тогда окончательно получим Зх<sup>2</sup> - 10x + 3 = (х - 3)(3х - 1). <br>Заметим, что заданный квадратный трехчлен можно разложить на множители и без применения теоремы 2, использовав способ группировки: <br> | + | [[Image:14-06-58.jpg]]<br><br>Есть смысл вместо [[Image:14-06-59.jpg]] написать Зx - 1. Тогда окончательно получим Зх<sup>2</sup> - 10x + 3 = (х - 3)(3х - 1). <br>Заметим, что заданный квадратный трехчлен можно разложить на множители и без применения теоремы 2, использовав способ группировки: <br> |
| | | | |
| - | Зх<sup>2</sup> - 10x + 3 = Зх<sup>2</sup> - 9х - х + 3 = <br>= Зх (х - 3) - (х - 3) = (х - 3) (Зx - 1). <br> | + | Зх<sup>2</sup> - 10x + 3 = Зх<sup>2</sup> - 9х - х + 3 = <br>= Зх (х - 3) - (х - 3) = (х - 3) (Зx - 1). <br> |
| | | | |
| - | Но, как видите, при этом способе успех зависит от того, сумеем ли мы найти удачную группировку или нет, тогда как при первом способе успех гарантирован. <br>'''Пример 1'''. Сократить дробь <br> | + | Но, как видите, при этом способе успех зависит от того, сумеем ли мы найти удачную группировку или нет, тогда как при первом способе успех гарантирован. <br>'''Пример 1'''. Сократить дробь <br> |
| | | | |
| - | [[Image:14-06-60.jpg]]<br><br>Решение. Из уравнения 2х<sup>2</sup> + 5х + 2 = 0 находим х<sub>1</sub> = - 2, <br> | + | [[Image:14-06-60.jpg]]<br><br>Решение. Из уравнения 2х<sup>2</sup> + 5х + 2 = 0 находим х<sub>1</sub> = - 2, <br> |
| | | | |
| - | [[Image:14-06-61.jpg]]<br><br>Из уравнения х2 - 4х - 12 = 0 находим х<sub>1</sub> = 6, х<sub>2</sub> = -2. Поэтому <br>х<sup>2</sup>- 4х - 12 = (х- 6) (х - (- 2)) = (х - 6) (х + 2). <br>А теперь сократим заданную дробь:<br> | + | [[Image:14-06-61.jpg]]<br><br>Из уравнения х2 - 4х - 12 = 0 находим х<sub>1</sub> = 6, х<sub>2</sub> = -2. Поэтому <br>х<sup>2</sup>- 4х - 12 = (х- 6) (х - (- 2)) = (х - 6) (х + 2). <br>А теперь сократим заданную дробь:<br> |
| | | | |
| - | [[Image:14-06-62.jpg]]<br><br>'''Пример 3'''. Разложить на множители выражения: <br>а)x4 + 5x<sup>2</sup>+6; б)2x+[[Image:14-06-63.jpg]]-3<br>Р е ш е н и е. а) Введем новую переменную у = х<sup>2</sup>. Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде у<sup>2</sup> + bу + 6. <br>Решив уравнение у<sup>2</sup> + bу + 6 = 0, найдем корни квадратного трехчлена у<sup>2</sup> + 5у + 6: у<sub>1</sub> = - 2, у<sub>2</sub> = -3. Теперь воспользуемся теоремой 2; получим<br> | + | [[Image:14-06-62.jpg]]<br><br>'''Пример 3'''. Разложить на множители выражения: <br>а)x4 + 5x<sup>2</sup>+6; б)2x+[[Image:14-06-63.jpg]]-3<br>Р е ш е н и е. а) Введем новую переменную у = х<sup>2</sup>. Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде у<sup>2</sup> + bу + 6. <br>Решив уравнение у<sup>2</sup> + bу + 6 = 0, найдем корни квадратного трехчлена у<sup>2</sup> + 5у + 6: у<sub>1</sub> = - 2, у<sub>2</sub> = -3. Теперь воспользуемся теоремой 2; получим<br> |
| | | | |
| - | у<sup>2</sup> + 5у + 6 = (у + 2) (у + 3). <br>Осталось вспомнить, что у = x<sup>2</sup> , т. е. вернуться к заданному выражению. Итак, <br>x<sup>4</sup> + 5х<sup>2</sup>+ 6 = (х<sup>2</sup> + 2)(х<sup>2</sup> + 3). <br>б) Введем новую переменную у = [[Image:14-06-63.jpg]]. Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде 2у<sup>2</sup> + у - 3. Решив уравнение <br>2у<sup>2</sup> + у - 3 = 0, найдем корни квадратного трехчлена 2у<sup>2</sup> + у - 3: <br>y<sub>1</sub> = 1, y<sub>2</sub>= [[Image:14-06-64.jpg]]. Далее, используя теорему 2, получим: <br> | + | у<sup>2</sup> + 5у + 6 = (у + 2) (у + 3). <br>Осталось вспомнить, что у = x<sup>2</sup> , т. е. вернуться к заданному выражению. Итак, <br>x<sup>4</sup> + 5х<sup>2</sup>+ 6 = (х<sup>2</sup> + 2)(х<sup>2</sup> + 3). <br>б) Введем новую переменную у = [[Image:14-06-63.jpg]]. Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде 2у<sup>2</sup> + у - 3. Решив уравнение <br>2у<sup>2</sup> + у - 3 = 0, найдем корни квадратного трехчлена 2у<sup>2</sup> + у - 3: <br>y<sub>1</sub> = 1, y<sub>2</sub>= [[Image:14-06-64.jpg]]. Далее, используя теорему 2, получим: <br> |
| | | | |
| - | [[Image:14-06-65.jpg]]<br><br>Осталось вспомнить, что у = [[Image:14-06-63]] , т. е. вернуться к заданному выражению. Итак, <br> | + | [[Image:14-06-65.jpg]]<br><br>Осталось вспомнить, что у = , т. е. вернуться к заданному выражению. Итак, <br> |
| | | | |
| | [[Image:14-06-66.jpg]]<br><br>В заключение параграфа — некоторые рассуждения, опятьтаки связанные с теоремой Виета, а точнее, с обратным утверждением: <br>если числа х<sub>1</sub>, х<sub>2</sub> таковы, что х<sup>1</sup> + х<sup>2</sup> = - р, x<sub>1</sub>x<sub>2</sub> = q, то эти числа — корни уравнения <br>С помощью этого утверждения можно решать многие квадратные уравнения устно, не пользуясь громоздкими формулами корней, а также составлять квадратные уравнения с заданными корнями. Приведем примеры. | | [[Image:14-06-66.jpg]]<br><br>В заключение параграфа — некоторые рассуждения, опятьтаки связанные с теоремой Виета, а точнее, с обратным утверждением: <br>если числа х<sub>1</sub>, х<sub>2</sub> таковы, что х<sup>1</sup> + х<sup>2</sup> = - р, x<sub>1</sub>x<sub>2</sub> = q, то эти числа — корни уравнения <br>С помощью этого утверждения можно решать многие квадратные уравнения устно, не пользуясь громоздкими формулами корней, а также составлять квадратные уравнения с заданными корнями. Приведем примеры. |
| Строка 57: |
Строка 57: |
| | 5) х<sup>2</sup> - 293x + 2830 = 0. Здесь х<sub>1</sub>+ х<sub>2</sub> = 293, х<sub>1</sub>х<sub>2</sub> = 2830. Если обратить внимание на то, что 2830 = 283 • 10, а 293 = 283 + 10, то становится ясно, что х<sub>1</sub> = 283, х<sub>2</sub> = 10 (а теперь представьте, какие вычисления пришлось бы выполнить для решения этого квадратного уравнения с помощью стандартных формул). | | 5) х<sup>2</sup> - 293x + 2830 = 0. Здесь х<sub>1</sub>+ х<sub>2</sub> = 293, х<sub>1</sub>х<sub>2</sub> = 2830. Если обратить внимание на то, что 2830 = 283 • 10, а 293 = 283 + 10, то становится ясно, что х<sub>1</sub> = 283, х<sub>2</sub> = 10 (а теперь представьте, какие вычисления пришлось бы выполнить для решения этого квадратного уравнения с помощью стандартных формул). |
| | | | |
| - | 6) Составим квадратное уравнение так, чтобы его корнями служили числа х<sub>1</sub> = 8, х<sub>2</sub> = - 4. Обычно в таких случаях составляют приведенное квадратное уравнение х<sup>2</sup> + рх + q = 0. <br>Имеем х<sub>1</sub>+ х<sub>2</sub>= -р, поэтому 8 - 4 = -р, т. е. р = -4. Далее, х<sub>1</sub>х<sub>2</sub>= q, т.е. 8«(-4) = q, откуда получаем q = -32. Итак, р = -4, q = -32, значит, искомое квадратное уравнение имеет вид х<sup>2</sup>-4х-32 = 0. <br><br><br><br><br><br><br> | + | 6) Составим квадратное уравнение так, чтобы его корнями служили числа х<sub>1</sub> = 8, х<sub>2</sub> = - 4. Обычно в таких случаях составляют приведенное квадратное уравнение х<sup>2</sup> + рх + q = 0. <br>Имеем х<sub>1</sub>+ х<sub>2</sub>= -р, поэтому 8 - 4 = -р, т. е. р = -4. Далее, х<sub>1</sub>х<sub>2</sub>= q, т.е. 8«(-4) = q, откуда получаем q = -32. Итак, р = -4, q = -32, значит, искомое квадратное уравнение имеет вид х<sup>2</sup>-4х-32 = 0. <br><br><br><br><br><br><br> |
| - | | + | |
| - | <br> | + | |
| | | | |
| | + | <br> |
| | | | |
| | + | <br> |
| | | | |
| | <sub>Математика за 8 класс бесплатно [[Математика|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Математика за 8 класс бесплатно [[Математика|скачать]], планы конспектов уроков, готовимся к школе [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
Версия 07:41, 14 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Теорема Виета
ТЕОРЕМА ВИЕТА
В этом параграфе мы познакомимся с любопытными соотношениями между корнями квадратного уравнения и его коэффициентами. Эти соотношения впервые обнаружил французский математик Франсуа Виет (1540—1603).

Например, для уравнения Зx2 - 8x - 6 = 0, не находя его корней, можно, воспользовавшись теоремой Виета, сразу сказать, что сумма корней равна 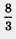 , а произведение корней равно , а произведение корней равно 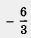
т. е. - 2. А для уравнения х2 - 6х + 8 = 0 заключаем: сумма корней равна 6, произведение корней равно 8; между прочим, здесь нетрудно догадаться, чему равны корни: 4 и 2.
Доказательство теоремы Виета. Корни х1 и х2 квадратного уравнения ах2 + bх + с = 0 находятся по формулам
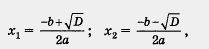
где D = b2 — 4ас — дискриминант уравнения. Сложив эти корни,
получим
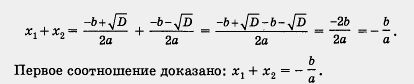
Теперь вычислим произведение корней х1 и х2 Имеем
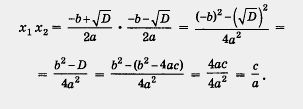
Второе соотношение доказано: 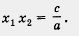
Замечание. Теорема Виета справедлива и в том случае, когда квадратное уравнение имеет один корень (т. е. когда D = 0), просто в этом случае считают, что уравнение имеет два одинаковых корня, к которым и применяют указанные выше соотношения.
Особенно простой вид принимают доказанные соотношения для приведенного квадратного уравнения х2 + рх + q = 0. В этом случае получаем:
x1 = x2 = -p, x1x2 =q
т.е. сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
С помощью теоремы Виета можно получить и другие соотношения между корнями и коэффициентами квадратного уравнения. Пусть, например, х1 и х2 — корни приведенного квадратного уравнения х2 + рх + q = 0. Тогда
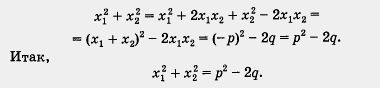
Однако основное назначение теоремы Виета не в том, что она выражает некоторые соотношения между корнями и коэффициентами квадратного уравнения. Гораздо важнее то, что с помощью теоремы Виета выводится формула разложения квадратного трехчлена на множители, без которой мы в дальнейшем не обойдемся.
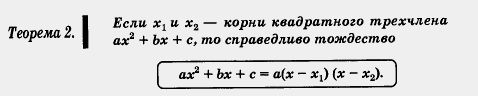
Доказательство. Имеем
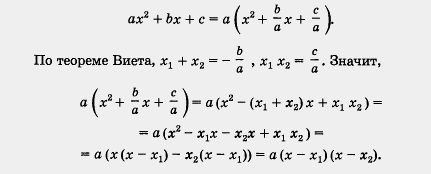
Пример 1. Разложить на множители квадратный трехчлен Зх2 - 10x + 3.
Решение. Решив уравнение Зх2 - 10x + 3 = 0, найдем корни квадратного трехчлена Зх2 - 10x + 3: х1 = 3, х2 = 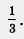 . .
Воспользовавшись теоремой 2, получим
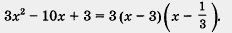
Есть смысл вместо 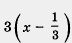 написать Зx - 1. Тогда окончательно получим Зх2 - 10x + 3 = (х - 3)(3х - 1). написать Зx - 1. Тогда окончательно получим Зх2 - 10x + 3 = (х - 3)(3х - 1).
Заметим, что заданный квадратный трехчлен можно разложить на множители и без применения теоремы 2, использовав способ группировки:
Зх2 - 10x + 3 = Зх2 - 9х - х + 3 =
= Зх (х - 3) - (х - 3) = (х - 3) (Зx - 1).
Но, как видите, при этом способе успех зависит от того, сумеем ли мы найти удачную группировку или нет, тогда как при первом способе успех гарантирован.
Пример 1. Сократить дробь
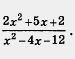
Решение. Из уравнения 2х2 + 5х + 2 = 0 находим х1 = - 2,
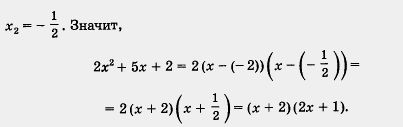
Из уравнения х2 - 4х - 12 = 0 находим х1 = 6, х2 = -2. Поэтому
х2- 4х - 12 = (х- 6) (х - (- 2)) = (х - 6) (х + 2).
А теперь сократим заданную дробь:
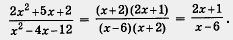
Пример 3. Разложить на множители выражения:
а)x4 + 5x2+6; б)2x+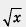 -3 -3
Р е ш е н и е. а) Введем новую переменную у = х2. Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде у2 + bу + 6.
Решив уравнение у2 + bу + 6 = 0, найдем корни квадратного трехчлена у2 + 5у + 6: у1 = - 2, у2 = -3. Теперь воспользуемся теоремой 2; получим
у2 + 5у + 6 = (у + 2) (у + 3).
Осталось вспомнить, что у = x2 , т. е. вернуться к заданному выражению. Итак,
x4 + 5х2+ 6 = (х2 + 2)(х2 + 3).
б) Введем новую переменную у = 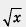 . Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде 2у2 + у - 3. Решив уравнение . Это позволит переписать заданное выражение в виде квадратного трехчлена относительно переменной у, а именно в виде 2у2 + у - 3. Решив уравнение
2у2 + у - 3 = 0, найдем корни квадратного трехчлена 2у2 + у - 3:
y1 = 1, y2= 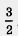 . Далее, используя теорему 2, получим: . Далее, используя теорему 2, получим:
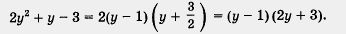
Осталось вспомнить, что у = , т. е. вернуться к заданному выражению. Итак,
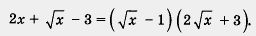
В заключение параграфа — некоторые рассуждения, опятьтаки связанные с теоремой Виета, а точнее, с обратным утверждением:
если числа х1, х2 таковы, что х1 + х2 = - р, x1x2 = q, то эти числа — корни уравнения
С помощью этого утверждения можно решать многие квадратные уравнения устно, не пользуясь громоздкими формулами корней, а также составлять квадратные уравнения с заданными корнями. Приведем примеры.
1) х2 - 11х + 24 = 0. Здесь x1 + х2 = 11, х1х2 = 24. Нетрудно догадаться, что х1 = 8, х2 = 3.
2) х2 + 11х + 30 = 0. Здесь x1 + х2 = -11, х1х2 = 30. Нетрудно догадаться, что х1 = -5, х2 = -6.
Обратите внимание: если свободный член уравнения — положительное число, то оба корня либо положительны, либо отрицательны; это важно учитывать при подборе корней.
3) х2 + х - 12 = 0. Здесь x1 + х2 = -1, х1х2 = -12. Легко догадаться, что х1 = 3, х2 = -4.
Обратите внимание: если свободный член уравнения — отрицательное число, то корни различны по знаку; это важно учитывать при подборе корней.
4) 5х2 + 17x - 22 = 0. Нетрудно заметить, что х = 1 удовлетворяет уравнению, т.е. х1 = 1 — корень уравнения. Так как х1х2 = -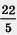 , а х1 = 1, то получаем, что х2 = - , а х1 = 1, то получаем, что х2 = -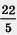 . .
5) х2 - 293x + 2830 = 0. Здесь х1+ х2 = 293, х1х2 = 2830. Если обратить внимание на то, что 2830 = 283 • 10, а 293 = 283 + 10, то становится ясно, что х1 = 283, х2 = 10 (а теперь представьте, какие вычисления пришлось бы выполнить для решения этого квадратного уравнения с помощью стандартных формул).
6) Составим квадратное уравнение так, чтобы его корнями служили числа х1 = 8, х2 = - 4. Обычно в таких случаях составляют приведенное квадратное уравнение х2 + рх + q = 0.
Имеем х1+ х2= -р, поэтому 8 - 4 = -р, т. е. р = -4. Далее, х1х2= q, т.е. 8«(-4) = q, откуда получаем q = -32. Итак, р = -4, q = -32, значит, искомое квадратное уравнение имеет вид х2-4х-32 = 0.
Математика за 8 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|