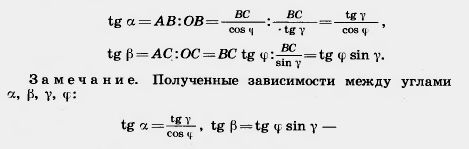|
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Трехгранный и многогранный угол
Трехгранный и многогранный угол
Рассмотрим три луча a, b, с, исходящие из одной точки и не лежащие в одной плоскости. Трехгранным углом (аbс) называется фигура, составленная из трех плоских углов (аb), (bс) и (aс) (рис. 400). Эти углы называются гранями трехгранного угла, а их стороны — ребрами . Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
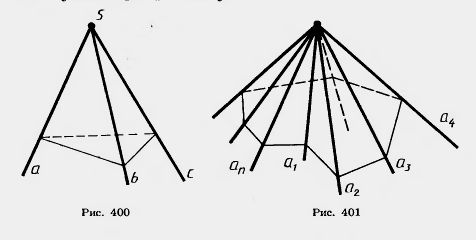
Аналогично определяется понятие многогранного угла (рис. 401).
Задача (2). У трехгранного угла (аЬс) двугранный угол при ребре с прямой, двугранный угол при ребре Ь равен 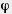 , а плоский угол (bс) равен , а плоский угол (bс) равен 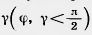 Найдите два других плоских угла: Найдите два других плоских угла:  = = (аb), (аb),  = = (ac). (ac).
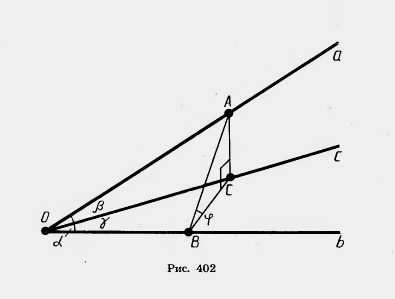
Решение. Опустим из произвольной точки А ребра a перпендикуляр АВ на ребро b и перпендикуляр АС на ребро с (рис. 402). По теореме о трех перпендикулярах СВ — перпендикуляр к ребру b.
Из прямоугольных треугольников ОАВ, ОСВ, АОС и ABC получаем:
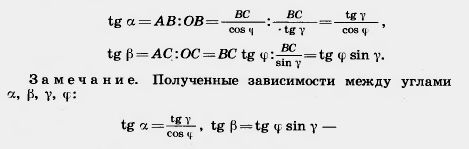
— позволяют, зная два угла, найти два других.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|