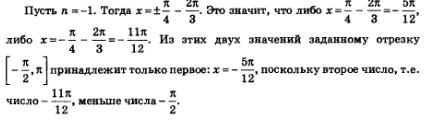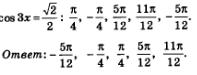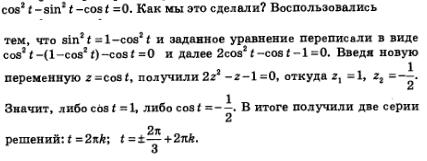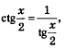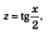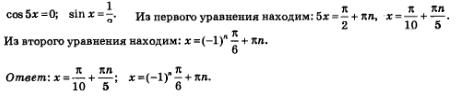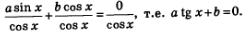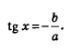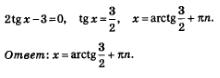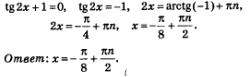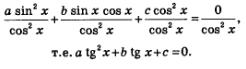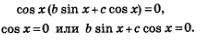Гипермаркет знаний>>Математика>>Математика 10 класс>> Тригонометрические уравнения

§ 20. Тригонометрические уравнения

Простейшие тригонометрические уравнения

Все уравнения, которые содержат переменную под знаком тригонометрических функций, называются тригонометрическим уравнением. Если перед вами уравнения такого вида, как:

sin x = a; cos x = a; tg x = a; ctg x = a,

в котором x является его переменной, и a является действительным числом, то такие уравнения называются простейшими тригонометрическими уравнениями. И если нам с вами известно, что в том случае, когда:

1) | а | < 1, то решения уравнения cos о:-а приобретает такой вот вид:

Во всех перечисленных формулах подразумевается, что параметр (n, к и т.д.) принимает любые целочисленные значения

Во всех этих формулах, которые перечислены выше, следует понимать, что параметр (n, к и т.д.) может принимать любые целочисленные значения.

Также к простейшим уравнениям можно отнести и такие уравнения, которые имеют вид: Т(кх + m)=а. В этом случае Т является знаком какой-нибудь тригонометрической функции. А теперь давайте попробуем это рассмотреть на примере решения уравнения.

Пример 1. Нам нужно решить данные уравнения:

Решение:

а) Для решения этого уравнения нам понадобиться в первую очередь ввести новую переменную:

Далее, мы вернемся к переменной х, и соответственно получим:

Теперь нам остается разделить почленно на два обе эти части, в итоге мы получим:

Но здесь обратите внимание на то, что приобретя некоторый опыт решения таких уравнений, появляется возможность без ввода промежуточной переменной t = 2х, сразу переходить от уравнения

Таким методом мы постараемся действовать и в дальнейшем.

б) Нам с вами уже известно, что при решении такого уравнения, как соs t = а, оно приобретает вид:

А это будет означать, что:

Рассмотрим второй пример.

Пример 2. Нам необходимо найти корни такого уравнения, как:

Эти корни принадлежат отрезку[0, п]. Приступим к решению.

Решение.

Внвчале мы с вами решим это уравнение в общем виде, руководствуясь примером 1а:

Теперь попробуем последовательно придать параметру п, такие значения, как: 0,1, 2,..., -1, -2,... , а далее возьмем и подставим эти значения в общую формулу корней. Смотрим, что у нас вышло:

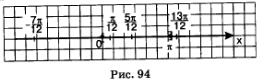
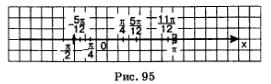
А получилось у нас то, что данное число не принадлежит заданному отрезку [0, п], также как и не принадлежать заданному отрезку и все те значения х, которые мы получили из общей формулы при n = -2, -3,... Сейчас внимательно посмотрите на рис. 94. На нем мы видим геометрическую интерпретацию проведенных рассуждений.

Решив уравнение и рассмотрев рисунок, мы с вами пришли к выводу, что заданному отрезку [0, п] могут принадлежать корни уравнения, полученные из общей формулы, если параметр n имеет следующие значения: n = 0, n = 1.

Вот как выглядят эти корни:

Следовательно, мы получаем такой ответ:

Перейдем к решению следующего примера.

Пример 3. Дано уравнение

и нам нужно найти корни, принадлежащие отрезку

Решение: В первую очередь нам нужно решить это уравнение в общем виде, взяв за пример решения задание 1б:

Далее необходимо придать последовательно параметру n, значения 0,1, 2,..., -1, -2,... Следующим нашим шагом нужно будет подставить все эти значения в общую формулу корней. Смотрим, вот что у нас вышло:

У нас получились числа, которые больше числа n. И мы снова приходим к выводу, что значения х, которые мы получили из общей формулы при n = 3,4,..., тем более не могут принадлежать заданному отрезку.

Так же, как и не могут принадлежать отрезку значения х, полученные из общей формулы, если n = -2, - 3,...

Рассмотрите внимательно представленную на рис. 95 интерпретацию проведенных рассуждений.

Из этого следует, что заданному отрезку

принадлежат такие корни уравнения, как:

Два основных метода решения тригонометрических уравнений

А сейчас мы с вами перейдем к рассмотрению основных методов решения тригонометрических уравнений. Для этих целей, как правило, используют:

• во-первых, метод введения новой переменной;
• во-вторых, способ разложения на множители.

А сейчас давайте вернемся немного назад и вспомним, как на третьем примере мы с вами решили тригонометрическое уравнение:

Вспомним, что мы сделали в первую очередь. Во-первых, ввели новую переменную ю z = sin t, а потом переписали уравнение, которое приобрело такой вид:

В итоге, мы с вами получили два простых уравнения:

Из сделанных ранее выводов мы увидели, что первое уравнение не имеет решения. А вот второе имеет их целых два:

Далее мы увидели, что их можно объединить одной формулой

Вспомните, как было решено это тригонометрическое уравнение:

Пример 4. Решим следующее уравнение.

Решение.

Возьмем уравнение:

Попробуем в него ввести новую переменную:

Смотрим, что это нам даст. А это нам позволит записать уравнение, которое имеет более простой вид:

Смотрим, что мы имеем:

Теперь вернемся к переменной х, ну и в итоге получим уже два уравнения:

С методом введения новой переменной мы уже выяснили, а сейчас попробуем решить тригонометрическое уравнение вторым способом, методом разложения на множители. В принципе, с этим методом вы также знакомы.

Берем уравнение f(х) =0 и пробуем преобразовать его к такому виду:

Для этого нам нужно решить два уравнения:

Пример 5. В следующем примере решение задачи также сводится к решению совокупности уравнений

Решение.

И соответственно из этих уравнений у нас выходит:

Пример 6. Следующее уравнение решаем по такому же принципу.

Решение.

Нам дано следующее уравнение:

Следовательно, приходим к совокупности уравнений:

Замечание. Тут необходимо учесть то, что не всегда переход от уравнения:

к совокупности уравнений:

Является безопасным.

Например, берем уравнение:

С помощью уравнения tg x = 0 находим х = пn, а из уравнения sin x = 1 находим

Но здесь присутствует одно «но», так как включить обе серии решений в ответ нельзя.

Так как при значении

Его множитель tg х не имеет смысла, другими словами он не имеет значения, так как не является областью определения уравнения, т.е. – это посторонние корни.

[[Image:Alga377.jpg|80px|Формула]

Однородные тригонометрические уравнения

Теперь давайте рассмотрим и тригонометрические уравнения, которые имеют специальный вид, но встречаются довольно таки часто.

Определение. Уравнение, имеющее вид:

называется однородным тригонометрическим уравнением 1-й степени; а уравнение, которое выглядит так:

является однородным тригонометрическим уравнением 2-й степени.

Уравнения 1-й степени

Давайте рассмотрим общий случай решения тригонометрических уравнений, в котором коэффициенты а и b отличны от нуля, ведь при а =0, уравнение будет иметь вид

а такое уравнение мы обсуждать не будем, так же, как и при b=0 получаем sin х =0.

Нам дано уравнение:

Делим его части почленно на соs x, и получим:

Вот мы и пришли к простейшему тригонометрическому уравнению

Внимание! Следует запомнить, что делить обе части уравнения на одно и то же выражение можно только в случае, если это выражение нигде не обращается в нуль. А вот как в этом убедиться?

Пример 7. Давайте решим уравнение 2 sin х - 3соs х = 0.

Решение. Разделим почленно на соs х, обе части уравнения и у нас получится:

Пример 8. Дано уравнение 2x + соs2x =0. Решение. Разделим почленно на соs 2 x обе части уравнения и получим:

Теперь приступим к однородному тригонометрическому уравнению 2-й степени:

Если в данном уравнении содержится член sin 2 х, у которого коэффициент отличный от 0, то при интересующих нас значениях переменной соs х не обращается в нуль, и следовательно обе части уравнения можно разделить почленно на соs 2 х. И вот что мы получим:

А получили мы квадратное уравнение относительно новой переменной z = tg х. Если в однородном тригонометрическом уравнении:

коэффициент а = 0, т.е. отсутствует член sin2 х. Тогда мы получим такое уравнение:

И решаем его методом разложения на множители:

У нас получается два уравнения. Также обстоит дело, когда с = 0, т.е. когда однородное уравнение имеет вид, где sin х можно вынести за скобки.

Фактически мы с вами получили

А.Г. Мордкович Алгебра 10 класс