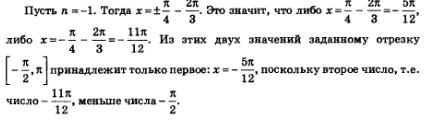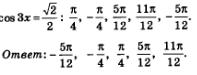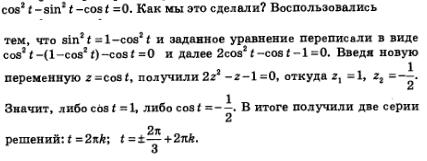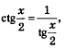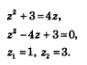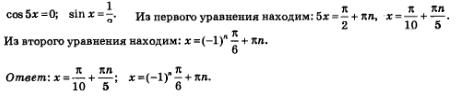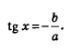|
|
|
| Строка 15: |
Строка 15: |
| | [[Image:Alga344.jpg]]<br>Итак, заданному отрезку [0, п] принадлежат те корни уравнения, которые получаются из общей формулы при следующих значениях параметра n: n = 0, n = 1. Эти корни таковы[[Image:Alga345.jpg]]<br>'''Ответ:''' [[Image:Alga345.jpg]]<br> | | [[Image:Alga344.jpg]]<br>Итак, заданному отрезку [0, п] принадлежат те корни уравнения, которые получаются из общей формулы при следующих значениях параметра n: n = 0, n = 1. Эти корни таковы[[Image:Alga345.jpg]]<br>'''Ответ:''' [[Image:Alga345.jpg]]<br> |
| | | | |
| - | '''Пример 3. '''Найти те корни уравнения [[Image:alga346.jpg]] которые принадлежат отрезку [[Image:alga347.jpg]]<br>'''Решение:''' Сначала решим уравнение в общем виде: [[Image:alga348.jpg]] (см. пример 16). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней.<br>[[Image:alga349.jpg]] , поскольку оба они больше числа л. Тем более не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = 3,4,... | + | '''Пример 3. '''Найти те корни уравнения [[Image:Alga346.jpg]] которые принадлежат отрезку [[Image:Alga347.jpg]]<br>'''Решение:''' Сначала решим уравнение в общем виде: [[Image:Alga348.jpg]] (см. пример 16). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней.<br>[[Image:Alga349.jpg]] , поскольку оба они больше числа л. Тем более не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = 3,4,... |
| | | | |
| - | [[Image:alga350.jpg]]<br>Не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = -2, - 3,...<br>На рис. 95 представлена геометрическая интерпретация проведенных рассуждений. | + | [[Image:Alga350.jpg]]<br>Не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = -2, - 3,...<br>На рис. 95 представлена геометрическая интерпретация проведенных рассуждений. |
| | | | |
| - | [[Image:alga351.jpg]]<br>Итак, заданному отрезку [[Image:alga352.jpg]] принадлежат следующие корни уравнения | + | [[Image:Alga351.jpg]]<br>Итак, заданному отрезку [[Image:Alga352.jpg]] принадлежат следующие корни уравнения |
| | | | |
| - | [[Image:alga353.jpg]] | + | [[Image:Alga353.jpg]] |
| | | | |
| - | '''2. Два основных метода решения тригонометрических уравнений'''<br>Для решения тригонометрических уравнений чаще всего используются два метода: введения новой переменной и разложения на множители.<br>Вернемся к материалу § 16. Там в примере 3 мы решили тригонометрическое уравнение [[Image:alga354.jpg]] Как мы это сделали? Ввели новую переменную z = sin t, переписали уравнение в виде<br>[[Image:alga355.jpg]] В результате мы получили два простых уравнения: [[Image:alga356.jpg]] Первое уравнение не имеет решений, а для второго нашли две серии решений: | + | '''2. Два основных метода решения тригонометрических уравнений'''<br>Для решения тригонометрических уравнений чаще всего используются два метода: введения новой переменной и разложения на множители.<br>Вернемся к материалу § 16. Там в примере 3 мы решили тригонометрическое уравнение [[Image:Alga354.jpg]] Как мы это сделали? Ввели новую переменную z = sin t, переписали уравнение в виде<br>[[Image:Alga355.jpg]] В результате мы получили два простых уравнения: [[Image:Alga356.jpg]] Первое уравнение не имеет решений, а для второго нашли две серии решений: |
| | | | |
| - | [[Image:alga357.jpg]] и установили (см. § 18), что эти две серии можно объединить одной формулой [[Image:alga358.jpg]]<br>В том же § 16 в примере 4 мы решили тригонометрическое уравнение | + | [[Image:Alga357.jpg]] и установили (см. § 18), что эти две серии можно объединить одной формулой [[Image:Alga358.jpg]]<br>В том же § 16 в примере 4 мы решили тригонометрическое уравнение |
| | | | |
| - | [[Image:alga359.jpg]] | + | [[Image:Alga359.jpg]] |
| | | | |
| - | '''Пример 4. '''Решить уравнение | + | '''Пример 4. '''Решить уравнение |
| | | | |
| - | [[Image:alga360.jpg]] | + | [[Image:Alga360.jpg]] |
| | | | |
| - | '''Решение.''' Поскольку [[Image:alga361.jpg]] есть смысл ввести новую переменную [[Image:alga362.jpg]] Это позволит переписать уравнение в более простом виде: [[Image:alga363.jpg]]<br>Имеем: | + | '''Решение.''' Поскольку [[Image:Alga361.jpg]] есть смысл ввести новую переменную [[Image:Alga362.jpg]] Это позволит переписать уравнение в более простом виде: [[Image:Alga363.jpg]]<br>Имеем: |
| | | | |
| - | <br>г2+3=4г, г2 -42 + 3=0, 2! =1, г2 =3.<br>х<br>Возвращаясь к переменной х9 получаем два уравнения: = 1 или<br>X X X тс<br>= 3. Из первого уравнения находим: — = агс1§ 1 + тел, т.е. —= —+ял,<br>К X<br>х=— + 2тсл. Из второго уравнения находим: — = агс1§ 3 + яп, х =2агс{§ 3 + 2ял. 2 2 тс<br>Ответ: х = — + 2пп, лс=2агс(еЗ + 2тсл. 2<br>V^Теперь поговорим о втором методе решения тригонометрических уравнений — методе разложения на множители. Смысл этого метода вам знаком: если уравнение х) =0 возможно преобразовать к виду /, (х) /2(х) =0, то задача сводится к решению двух уравнений (обычно говорят — к решению совокупности уравнений):<br>А(*)=0; /2(х)=0. Пример 5. Решить уравнение ||созх + ^|=0.<br>Решение. Задача сводится к решению совокупности уравнений:<br>1 2<br>81ПЛС = -; СОЗ X = —.<br>3 5<br>Из этих уравнений находим соответственно:<br>1 2 х =(-1)"агсзш- + ял; х = ± агссоз(—)+2ял. <И]<br>3 5<br>Пример 6. Решить уравнение 2 зт х соз 5х - соз 5х=0. Решение. Имеем со85лс(28тл<;-1)=0. Значит, приходим к совокупности уравнений:<br>„ „ . 1 соз 5х = 0; 81П х=—.<br>2<br>„ я я тсп<br>Из первого уравнения находим :5х = — + я л, ж = —+ —.<br>я<br>Из второго уравнения находим: х =(-1)" — + ял.<br>6<br>Л я ял , „,„ я<br>Ответ: х=— + —; дс =(—1) — + ял. 10 5 ^ ' 6<br>Замечание. Учтите, что переход от уравнения ^(лс)-Ц(х)=0 к совокупности уравнений: ^(х)=0;^(х)=0 не всегда безопасен. Рассмотрим, например, уравнение х(зтх-1)=0. Из уравнения 1б*=0 находим<br>я<br>х = ял; из уравнения зтл: = 1 находим лс = —+ 2ял. Но включить обе серии<br>я<br>решений в ответ нельзя. Дело в том, что при значениях х = — + 2ял.входя-<br>94<br>щий в заданное уравнение множитель х не имеет смысла, т.е. значения<br>ж<br>х = — + 2пп не принадлежат области определения уравнения (области допустимых значений уравнения — ОДЗ), это — посторонние корни.<br>3. Однородные тригонометрические уравнения<br>Здесь мы познакомимся с довольно часто встречающимися на практике тригонометрическими уравнениями специального вида.<br>Определение. Уравнение вида: аз1пх + Ьсозх =0 называют однородным тригонометрическим уравнением первой степени; уравне-н ие вида: азю2 х + Ьз1п х соз х + с соз2 х = 0 называют однородным тригонометрическим уравнением второй степени.<br>Сначала поговорим о решении однородных тригонометрических уравнений первой степени, причем рассмотрим только самый общий случай, когда оба коэффициента а и Ъ отличны от нуля, так как, если а =0, уравнение принимает вид Ьсоз х=0, т.е. соз х=0 — такое уравнение отдельного обсуждения не заслуживает; аналогично при Ь=0 получаем зт х =0, что тоже не требует отдельного обсуждения.<br>Итак, дано уравнение азтх+Ьсозх=0, где а * 0,Ь * 0. Разделив обе части уравнения почленно на соз*, получим:<br>азтзс Ьсозх 0 , Л<br>-+-=-, т.е. а1%х+Ъ=0.<br>соз х соз х со&х<br>В итоге приходим к простейшему тригонометрическому уравнению<br>Ъ<br>= —. а<br>Внимание! Вообще-то делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя). Уверены ли мы, что в нашем уравнении соз х отличен от нуля? Давайте проанализируем. Предположим, что соз х =0. Тогда однородное уравнение а зтх+Ь соз х=0 примет вида зтдг=0, т.е. зщх=0 (вы ведь не забыли, что коэффициент а отличен от нуля). Получается, что и соз х=0, и зш л: =0, а это невозможно, так как зтх и соззс обращаются в нуль в различных точках. Итак, в однородном тригонометрическом уравнении первой степени деление обеих частей уравнения насозх— вполне благополучная операция.<br>Уравнения вида а зт тх+Ь соз тх=0 тоже называют однородными тригонометрическими уравнениями первой степени. Для их решения обе части уравнения делят почленно на соз тх.<br>Пример 7. Решить уравнение2 зт х-3соз х=0.<br>Решение. Разделив обе части уравнения почленно на соз х, получим:<br>95<br>3 3<br>21§лс-3=0, л: = —, лс = агс 1%- + пп.<br>2 2<br>3<br>Ответ: х = агс1е- + пп.<br>2<br>Пример 8. Решить уравнение 8т2лс + со82лс =0.<br>Решение. Разделив обе части уравнения почленно насо82лс, получим: 182*+ 1=0, 1&2х=-1, 2х = агс1ё(-1)+ пп,<br>„л п пп<br>2х = — + пп, х = — + —.<br>4 8 2<br>^ п пп<br>Ответ: х ----1--.<br>8 2_^<br>Рассмотрим теперь однородное тригонометрическое уравнение второй степени:<br>а 81П2 х+Ь 81П x соз Х+С соз2 X =0.<br>Если коэффициент а отличен от нуля, т.е. в уравнении содержится член зт2 х с каким-то коэффициентом, отличным от нуля, то, рассуждая как и выше, нетрудно убедиться в том, что при интересующих нас значениях переменной сое хне обращается в нуль, а потому можно обе части уравнения разделить почленно на сое2 х. Что это даст? Смотрите:<br>а 81п2 X Ь 81п X соз X С соз2 X 0<br>сов2 X соз2 X сов2 X соз2 X<br>т.е. а 1§2х+Ь х+с =0.<br>Это — квадратное уравнение относительно новой переменной г = 1%х.<br>Пусть теперь в однородном тригонометрическом уравнении<br>а 81п2 Х + Ь 81п X соз Х + С соз2 X =0<br>коэффициент а равен 0, т.е. отсутствует член азт2 х. Тогда уравнение принимает вид:<br>Ь 81п X соз х + ссоз2 Х = 0.<br>Это уравнение можно решить методом разложения на множители: с08 X (Ъ 81п Х + С соз X) =0, соз X = 0 или Ъ 81п Х + С соз X =0.<br>Получились два уравнения, которые мы с вами решать умеем. Аналогично обстоит дело и в случае, когдас =0, т.е. когда однородное уравнение имеет вид а зт2 х+Ь зт х соз х=0 (здесь можно вынести за скобки зтх).<br>Фактически мы выработали<br>96<br>АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ автгх+Ь 81П хсоз х+ссоа2 х=0:<br>1. Посмотреть, есть ли в уравнении член азт2 х.<br>2. Если членавт2 хв уравнении содержится (т.е. а Ф 0), то уравнение решается делением обеих его частей на сое2 х и последующим введением новой переменной г = х.<br>3. Если член азт2 х в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят совх.<br>Так же обстоит дело и в однородных уравнениях вида: а 81П2 тх+Ъ 8111 тхсовтх+с сов2 тх=0.<br>Пример 9. Решить уравнение<br>81П2 лс - 3 81П л: соз х+ 2 сое2 х = 0.<br>Решение. Разделив обе част^ уравнения почленно на соз2 х, получим 1^х-31§ х + 2=0. Введя новую переменную г=Щх, получим г2 -Зг + 2=0, откуда находим г1 = 1, г2 =2. Значит, либо {%х = 1, либо 1%х=2. Из первого уравнения находим:<br>х = агс1ё 1 + пп, т.е. х = — + пп.<br>Из второго уравнения находим: х = агс1§ 2 + пп. п<br>Ответ: х = — + пп\ х = агс1§ 2 + пп. 4<br>Пример 10. Решить уравнение<br>•у/Ззтлссовлс + соз2 х=0.<br>Решение. Здесь отсутствует член вида а зш2 х, значит, делить обе части уравнения на соз2 х нельзя. Решим уравнение методом разложения на множители. Имеем:<br>совх(4з 8Н1л; + со8л;)=0, т.е. соз х = 0 или 73 зш х + соз х=0.<br>тт я<br>Из первого уравнения находим х = — + кп.<br>Второе уравнение — однородное тригонометрическое уравнение первой степени. Решим его с помощью почленного деления обеих частей уравнения насозлс:<br>81пя; + Со8я;=0,<br>4З^х + 1=0;<br>-П п<br>—Г= + пп,х = — + пп. л/3 6<br>1е л: = —Дг, откуда х = агс1§<br>4з<br>Ответ: х = — + пп: х = -—+пп. 2 6<br>В заключение рассмотрим более сложный пример.<br>4 Мордкович «Алгебра, 10 кл.»<br>97<br>Пример 11. Решить уравнение<br>3 81 п2 Зле - 2л/3 81Г1 Зх сое Зле + 5 сое2 Зле = 2 и выделить те его корни, которые принадлежат интервалу (-л, л).<br>Решение. Чем это уравнение сложнее предыдущих? Во-первых, оно не является однородным, так как в правой его части содержится не 0, а 2. Во-вторых, в левой части уравнения под знаками синуса и косинуса находится не х, а Зле. В-третьих, нужно не только решить уравнение в общем виде, но и выбрать корни, принадлежащие заданному промежутку. Эти три дополнительные трудности мы сейчас и начнем преодолевать.<br>С числом 2, содержащимся в правой части уравнения, мы поступим следующим образом. Известно, что зт21 + сое21 = 1 — это тождество верно для любого I. В частности, зт2 3* + сое2 Зле = 1. Но тогда 2 зт2 Зх + 2соз2 Зх =2. Заменив в правой части уравнения 2 на 2 81п2 Зле + 2со82 Зле, получим:<br>3 зт2 Зх - 273 зт Зх соа Зх + 5 соз2 Зх=2зт2Зх + 2 сов2 Зх.<br>Далее имеем:<br>3 зт2 Зх -2-Уз зт Зх соз Зх + 5сое2 3*'-2 зт2 Зх-2сов2 Зле = О, зт2 Зх-2^3 зт Зх соз Зле + Зсоз2 Зле =0.<br>Как видите, нам удалось преобразовать заданное уравнение в однородное тригонометрическое уравнение второй степени. Оно содержит в своем составе член зт2 Зх, значит, применив способ почленного деления на соз2 Зле, получим:<br>1§2 3 лс - 2-У31§ Зле + 3=0.<br>Положив г Зх, получим квадратное уравнение:<br>г2 -2л/3г +3=0.<br>Для решения этого уравнения можно использовать формулу корней квадратного уравнения, но изящнее сделать так: заметив, что<br>г2 -273г+3=(г-73)2, преобразовать квадратное уравнение к виду:<br>(г-7з)2=0,<br>и далее г--Уз =0.<br>Значит, 2 = л/5, т.е.<br>1§ЗХ = ТЗ, Зх = ап*8 -Уз + пп,<br>о 71<br>Злс = — + пп, 3<br>л пп<br>лс = - +-.<br>9 3<br>Осталось из найденной серии решений выбрать те корни уравнения, которые принадлежат заданному интервалу (-л, л). Можно осуществить «перебор по параметру», т.е. последовательно придать параметру п значения 0,1, 2,..., -1, -2,..., как мы это делали в п. 1 (примеры 2 иЗ). Но мы хотим показать вам еще один прием (быть может, он покажется вам более интересным).<br>98<br>Нам нужно найти такие значения х, которые содержатся в интервале (-л, л), т.е. удовлетворяют двойному неравенству -%<х<к. Поскольку л лл<br>х =— + —, получаем неравенство:<br>П ПП -л< —+-< л.<br>9 3<br>Умножив все части этого неравенства на 9 и разделив на тс, получим:<br>-9<1 + Зл<9, -10<3я<8,<br>10 8<br>--<п <-.<br>3 3<br>Осталось выяснить, какие целочисленные значения параметра п удовлетворяют последнему неравенству. Это значения: -3, -2, -1, 0,1, 2. Значит, если перечисленные шесть значений подставить вместо п в форте тел<br>мулу решении х = — н--, то мы тем самым и выделим интересующие нас<br>9 3<br>корни уравнения, принадлежащие заданному интервалу (-тс, тс). Итак:<br>1) если л = -3, то из формулы х=— + — получаем<br>9 3<br>п 8л<br>х =--л=--;<br>9 9<br>2) если л = -2, то из формулы х = — + — получаем<br>9 3<br>л _ 2л __ 5 л<br>3) если л = -1, то из формулы х + ^ получаем<br>_ л _ л _ 2 л<br>4) если л = 0, то из формулы + ~ получаем<br>л „ л<br>х=- + 0=~; 9 9<br>С\ 1 Я тел<br>5) если л = I, то из формулы х=—л--получаем<br>9 3 _ л я_4тс. *"9 + 3~~9~'<br>6) если л = 2, то из формулы х=— + — получаем<br>9 3<br>п 2тс 7тс<br>х=- +-=-.<br>9 3 9<br>^ 8л 5 л 2 л п 4тс 7п<br>Ответ:--;--;--; —; —.<br>9 9 9 9 9 9<br>4 й<br>99<br>
| + | [[Image:alga364.jpg]] |
| | + | |
| | + | Возвращаясь к переменной х получаем два уравнения: |
| | + | |
| | + | [[Image:alga365.jpg]] |
| | + | |
| | + | Теперь поговорим о втором методе решения тригонометрических уравнений — методе разложения на множители. Смысл этого метода вам знаком: если уравнение f(х) =0 возможно преобразовать к виду |
| | + | |
| | + | [[Image:alga366.jpg]] то задача сводится к решению двух уравнений (обычно говорят — к решению совокупности уравнений): |
| | + | |
| | + | [[Image:alga367.jpg]]<br>'''Пример 5.''' Решить уравнение [[Image:alga368.jpg]]<br>'''Решение. '''Задача сводится к решению совокупности уравнений: |
| | + | |
| | + | [[Image:alga369.jpg]]<br>Из этих уравнений находим соответственно: |
| | + | |
| | + | [[Image:alga370.jpg]]<br>'''Пример 6.''' Решить уравнение [[Image:alga371.jpg]]. |
| | + | |
| | + | '''Решение.''' Имеем [[Image:alga372.jpg]] Значит, приходим к совокупности уравнений: |
| | + | |
| | + | [[Image:alga373.jpg]]<br>'''Замечание.''' Учтите, что переход от уравнения [[Image:alga374.jpg]] к совокупности уравнений: [[Image:alga375.jpg]] не всегда безопасен. Рассмотрим, например, уравнение [[Image:alga376.jpg]] Из уравнения tg x = 0 находим<br>х = пn; из уравнения sin x = 1 находим [[Image:alga377.jpg]] Но включить обе серии решений в ответ нельзя. Дело в том, что при значениях [[Image:alga377.jpg]] входящий в заданное уравнение множитель tg х не имеет смысла, т.е. значения<br>[[Image:alga377.jpg]] не принадлежат области определения уравнения (области допустимых значений уравнения — ОДЗ), это — посторонние корни.<br>'''3. Однородные тригонометрические уравнения'''<br>Здесь мы познакомимся с довольно часто встречающимися на практике тригонометрическими уравнениями специального вида.<br>'''Определение.''' Уравнение вида: [[Image:alga378.jpg]] называют однородным тригонометрическим уравнением первой степени; уравнение вида: [[Image:alga379.jpg]] называют однородным тригонометрическим уравнением второй степени.<br>Сначала поговорим о решении однородных тригонометрических уравнений первой степени, причем рассмотрим только самый общий случай, когда оба коэффициента а и Ъ отличны от нуля, так как, если а =0, уравнение принимает вид [[Image:alga380.jpg]] такое уравнение отдельного обсуждения не заслуживает; аналогично при Ь=0 получаем sin х =0, что тоже не требует отдельного обсуждения.<br>Итак, дано уравнение [[Image:alga381.jpg]] Разделив обе части уравнения почленно на соs x, получим: |
| | + | |
| | + | [[Image:alga382.jpg]]<br>В итоге приходим к простейшему тригонометрическому уравнению |
| | + | |
| | + | [[Image:alga383.jpg]]<br>'''Внимание!''' Вообще-то делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя). Уверены ли мы, что в нашем уравнении соз х отличен от нуля? Давайте проанализируем. Предположим, что соз х =0. Тогда однородное уравнение а sin х+Ь соз х=0 примет вида зтдг=0, т.е. зщх=0 (вы ведь не забыли, что коэффициент а отличен от нуля). Получается, что и соз х=0, и зш л: =0, а это невозможно, так как зтх и соззс обращаются в нуль в различных точках. Итак, в однородном тригонометрическом уравнении первой степени деление обеих частей уравнения насозх— вполне благополучная операция.<br>Уравнения вида а зт тх+Ь соз тх=0 тоже называют однородными тригонометрическими уравнениями первой степени. Для их решения обе части уравнения делят почленно на соз тх.<br>'''Пример 7. '''Решить уравнение 2 sin х-3соз х=0.<br>'''Решение.''' Разделив обе части уравнения почленно на соз х, получим: |
| | + | |
| | + | <br>95<br>3 3<br>21§лс-3=0, л: = —, лс = агс 1%- + пп.<br>2 2<br>3<br>Ответ: х = агс1е- + пп.<br>2<br>Пример 8. Решить уравнение 8т2лс + со82лс =0.<br>Решение. Разделив обе части уравнения почленно насо82лс, получим: 182*+ 1=0, 1&2х=-1, 2х = агс1ё(-1)+ пп,<br>„л п пп<br>2х = — + пп, х = — + —.<br>4 8 2<br>^ п пп<br>Ответ: х ----1--.<br>8 2_^<br>Рассмотрим теперь однородное тригонометрическое уравнение второй степени:<br>а 81П2 х+Ь 81П x соз Х+С соз2 X =0.<br>Если коэффициент а отличен от нуля, т.е. в уравнении содержится член зт2 х с каким-то коэффициентом, отличным от нуля, то, рассуждая как и выше, нетрудно убедиться в том, что при интересующих нас значениях переменной сое хне обращается в нуль, а потому можно обе части уравнения разделить почленно на сое2 х. Что это даст? Смотрите:<br>а 81п2 X Ь 81п X соз X С соз2 X 0<br>сов2 X соз2 X сов2 X соз2 X<br>т.е. а 1§2х+Ь х+с =0.<br>Это — квадратное уравнение относительно новой переменной г = 1%х.<br>Пусть теперь в однородном тригонометрическом уравнении<br>а 81п2 Х + Ь 81п X соз Х + С соз2 X =0<br>коэффициент а равен 0, т.е. отсутствует член азт2 х. Тогда уравнение принимает вид:<br>Ь 81п X соз х + ссоз2 Х = 0.<br>Это уравнение можно решить методом разложения на множители: с08 X (Ъ 81п Х + С соз X) =0, соз X = 0 или Ъ 81п Х + С соз X =0.<br>Получились два уравнения, которые мы с вами решать умеем. Аналогично обстоит дело и в случае, когдас =0, т.е. когда однородное уравнение имеет вид а зт2 х+Ь зт х соз х=0 (здесь можно вынести за скобки зтх).<br>Фактически мы выработали<br>96<br>АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ автгх+Ь 81П хсоз х+ссоа2 х=0:<br>1. Посмотреть, есть ли в уравнении член азт2 х.<br>2. Если членавт2 хв уравнении содержится (т.е. а Ф 0), то уравнение решается делением обеих его частей на сое2 х и последующим введением новой переменной г = х.<br>3. Если член азт2 х в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят совх.<br>Так же обстоит дело и в однородных уравнениях вида: а 81П2 тх+Ъ 8111 тхсовтх+с сов2 тх=0.<br>Пример 9. Решить уравнение<br>81П2 лс - 3 81П л: соз х+ 2 сое2 х = 0.<br>Решение. Разделив обе част^ уравнения почленно на соз2 х, получим 1^х-31§ х + 2=0. Введя новую переменную г=Щх, получим г2 -Зг + 2=0, откуда находим г1 = 1, г2 =2. Значит, либо {%х = 1, либо 1%х=2. Из первого уравнения находим:<br>х = агс1ё 1 + пп, т.е. х = — + пп.<br>Из второго уравнения находим: х = агс1§ 2 + пп. п<br>Ответ: х = — + пп\ х = агс1§ 2 + пп. 4<br>Пример 10. Решить уравнение<br>•у/Ззтлссовлс + соз2 х=0.<br>Решение. Здесь отсутствует член вида а зш2 х, значит, делить обе части уравнения на соз2 х нельзя. Решим уравнение методом разложения на множители. Имеем:<br>совх(4з 8Н1л; + со8л;)=0, т.е. соз х = 0 или 73 зш х + соз х=0.<br>тт я<br>Из первого уравнения находим х = — + кп.<br>Второе уравнение — однородное тригонометрическое уравнение первой степени. Решим его с помощью почленного деления обеих частей уравнения насозлс:<br>81пя; + Со8я;=0,<br>4З^х + 1=0;<br>-П п<br>—Г= + пп,х = — + пп. л/3 6<br>1е л: = —Дг, откуда х = агс1§<br>4з<br>Ответ: х = — + пп: х = -—+пп. 2 6<br>В заключение рассмотрим более сложный пример.<br>4 Мордкович «Алгебра, 10 кл.»<br>97<br>Пример 11. Решить уравнение<br>3 81 п2 Зле - 2л/3 81Г1 Зх сое Зле + 5 сое2 Зле = 2 и выделить те его корни, которые принадлежат интервалу (-л, л).<br>Решение. Чем это уравнение сложнее предыдущих? Во-первых, оно не является однородным, так как в правой его части содержится не 0, а 2. Во-вторых, в левой части уравнения под знаками синуса и косинуса находится не х, а Зле. В-третьих, нужно не только решить уравнение в общем виде, но и выбрать корни, принадлежащие заданному промежутку. Эти три дополнительные трудности мы сейчас и начнем преодолевать.<br>С числом 2, содержащимся в правой части уравнения, мы поступим следующим образом. Известно, что зт21 + сое21 = 1 — это тождество верно для любого I. В частности, зт2 3* + сое2 Зле = 1. Но тогда 2 зт2 Зх + 2соз2 Зх =2. Заменив в правой части уравнения 2 на 2 81п2 Зле + 2со82 Зле, получим:<br>3 зт2 Зх - 273 зт Зх соа Зх + 5 соз2 Зх=2зт2Зх + 2 сов2 Зх.<br>Далее имеем:<br>3 зт2 Зх -2-Уз зт Зх соз Зх + 5сое2 3*'-2 зт2 Зх-2сов2 Зле = О, зт2 Зх-2^3 зт Зх соз Зле + Зсоз2 Зле =0.<br>Как видите, нам удалось преобразовать заданное уравнение в однородное тригонометрическое уравнение второй степени. Оно содержит в своем составе член зт2 Зх, значит, применив способ почленного деления на соз2 Зле, получим:<br>1§2 3 лс - 2-У31§ Зле + 3=0.<br>Положив г Зх, получим квадратное уравнение:<br>г2 -2л/3г +3=0.<br>Для решения этого уравнения можно использовать формулу корней квадратного уравнения, но изящнее сделать так: заметив, что<br>г2 -273г+3=(г-73)2, преобразовать квадратное уравнение к виду:<br>(г-7з)2=0,<br>и далее г--Уз =0.<br>Значит, 2 = л/5, т.е.<br>1§ЗХ = ТЗ, Зх = ап*8 -Уз + пп,<br>о 71<br>Злс = — + пп, 3<br>л пп<br>лс = - +-.<br>9 3<br>Осталось из найденной серии решений выбрать те корни уравнения, которые принадлежат заданному интервалу (-л, л). Можно осуществить «перебор по параметру», т.е. последовательно придать параметру п значения 0,1, 2,..., -1, -2,..., как мы это делали в п. 1 (примеры 2 иЗ). Но мы хотим показать вам еще один прием (быть может, он покажется вам более интересным).<br>98<br>Нам нужно найти такие значения х, которые содержатся в интервале (-л, л), т.е. удовлетворяют двойному неравенству -%<х<к. Поскольку л лл<br>х =— + —, получаем неравенство:<br>П ПП -л< —+-< л.<br>9 3<br>Умножив все части этого неравенства на 9 и разделив на тс, получим:<br>-9<1 + Зл<9, -10<3я<8,<br>10 8<br>--<п <-.<br>3 3<br>Осталось выяснить, какие целочисленные значения параметра п удовлетворяют последнему неравенству. Это значения: -3, -2, -1, 0,1, 2. Значит, если перечисленные шесть значений подставить вместо п в форте тел<br>мулу решении х = — н--, то мы тем самым и выделим интересующие нас<br>9 3<br>корни уравнения, принадлежащие заданному интервалу (-тс, тс). Итак:<br>1) если л = -3, то из формулы х=— + — получаем<br>9 3<br>п 8л<br>х =--л=--;<br>9 9<br>2) если л = -2, то из формулы х = — + — получаем<br>9 3<br>л _ 2л __ 5 л<br>3) если л = -1, то из формулы х + ^ получаем<br>_ л _ л _ 2 л<br>4) если л = 0, то из формулы + ~ получаем<br>л „ л<br>х=- + 0=~; 9 9<br>С\ 1 Я тел<br>5) если л = I, то из формулы х=—л--получаем<br>9 3 _ л я_4тс. *"9 + 3~~9~'<br>6) если л = 2, то из формулы х=— + — получаем<br>9 3<br>п 2тс 7тс<br>х=- +-=-.<br>9 3 9<br>^ 8л 5 л 2 л п 4тс 7п<br>Ответ:--;--;--; —; —.<br>9 9 9 9 9 9<br>4 й<br>99<br> |
| | | | |
| | А.Г. Мордкович Алгебра 10 класс | | А.Г. Мордкович Алгебра 10 класс |
Версия 09:21, 10 июля 2010
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика: Тригонометрические уравнения
§ 20. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
1. Простейшие тригонометрические уравнения
Тригонометрическими уравнениями обычно называют уравнения, в которых переменная содержится под знаками тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида a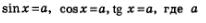 — действительное число. К настоящему моменту мы знаем, что: — действительное число. К настоящему моменту мы знаем, что:
1) если | а | < 1, то решения уравнения соз о:-а имеют вид:

Во всех перечисленных формулах подразумевается, что параметр (n, к и т.д.) принимает любые целочисленные значения 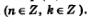
К простейшим относят обычно и уравнения вида Т(кх + m)=а, где Т — знак какой-либо тригонометрической функции.
Пример 1. Решить уравнения:
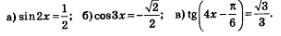
Решение: а) Введем новую переменную 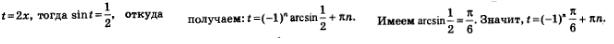
Возвращаясь к переменной х, получаем: 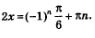 Осталось обе части этого равенства разделить почленно на 2; получим: Осталось обе части этого равенства разделить почленно на 2; получим:
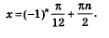
Заметим, что при наличии некоторого опыта можно не вводить промежуточную переменную t = 2х, а сразу переходить от уравнения 
Именно так мы и будем действовать в дальнейшем.
б) Мы знаем, что решения уравнения соs t = а имеют вид: Для нашего примера это означает, что Для нашего примера это означает, что

Пример 2. Найти те корни уравнения 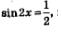 которые принадлежат отрезку[0, п]. которые принадлежат отрезку[0, п].
Решение. Сначала решим уравнение в общем виде: 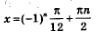 (см. пример 1а). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней. (см. пример 1а). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней.

Это число не принадлежит заданному отрезку [0, п]. Тем более не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при n = -2, -3,...
На рис. 94 представлена геометрическая интерпретация проведенных рассуждений.
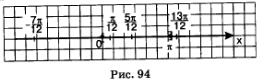
Итак, заданному отрезку [0, п] принадлежат те корни уравнения, которые получаются из общей формулы при следующих значениях параметра n: n = 0, n = 1. Эти корни таковы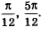
Ответ: 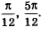
Пример 3. Найти те корни уравнения 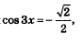 которые принадлежат отрезку которые принадлежат отрезку 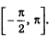
Решение: Сначала решим уравнение в общем виде: 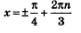 (см. пример 16). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней. (см. пример 16). Далее придадим параметру п последовательно значения 0,1, 2,..., -1, -2,... и подставим эти значения в общую формулу корней.
 , поскольку оба они больше числа л. Тем более не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = 3,4,... , поскольку оба они больше числа л. Тем более не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = 3,4,...
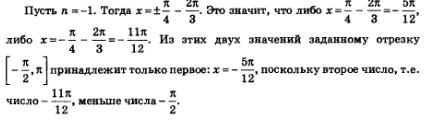
Не будут принадлежать заданному отрезку те значения х, которые получаются из общей формулы при п = -2, - 3,...
На рис. 95 представлена геометрическая интерпретация проведенных рассуждений.
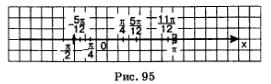
Итак, заданному отрезку 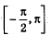 принадлежат следующие корни уравнения принадлежат следующие корни уравнения
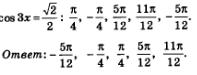
2. Два основных метода решения тригонометрических уравнений
Для решения тригонометрических уравнений чаще всего используются два метода: введения новой переменной и разложения на множители.
Вернемся к материалу § 16. Там в примере 3 мы решили тригонометрическое уравнение 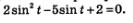 Как мы это сделали? Ввели новую переменную z = sin t, переписали уравнение в виде Как мы это сделали? Ввели новую переменную z = sin t, переписали уравнение в виде
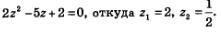 В результате мы получили два простых уравнения: В результате мы получили два простых уравнения: 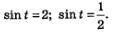 Первое уравнение не имеет решений, а для второго нашли две серии решений: Первое уравнение не имеет решений, а для второго нашли две серии решений:
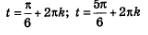 и установили (см. § 18), что эти две серии можно объединить одной формулой и установили (см. § 18), что эти две серии можно объединить одной формулой 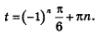
В том же § 16 в примере 4 мы решили тригонометрическое уравнение
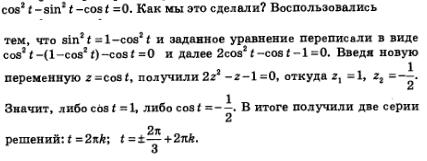
Пример 4. Решить уравнение
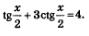
Решение. Поскольку 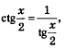 есть смысл ввести новую переменную есть смысл ввести новую переменную 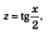 Это позволит переписать уравнение в более простом виде: Это позволит переписать уравнение в более простом виде: 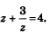
Имеем:
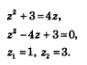
Возвращаясь к переменной х получаем два уравнения:

Теперь поговорим о втором методе решения тригонометрических уравнений — методе разложения на множители. Смысл этого метода вам знаком: если уравнение f(х) =0 возможно преобразовать к виду
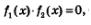 то задача сводится к решению двух уравнений (обычно говорят — к решению совокупности уравнений): то задача сводится к решению двух уравнений (обычно говорят — к решению совокупности уравнений):
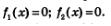
Пример 5. Решить уравнение 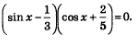
Решение. Задача сводится к решению совокупности уравнений:
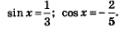
Из этих уравнений находим соответственно:
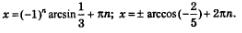
Пример 6. Решить уравнение 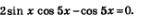 . .
Решение. Имеем 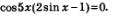 Значит, приходим к совокупности уравнений: Значит, приходим к совокупности уравнений:
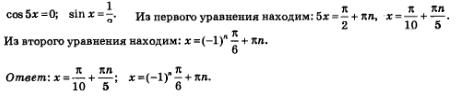
Замечание. Учтите, что переход от уравнения 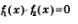 к совокупности уравнений: к совокупности уравнений: 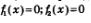 не всегда безопасен. Рассмотрим, например, уравнение не всегда безопасен. Рассмотрим, например, уравнение  Из уравнения tg x = 0 находим Из уравнения tg x = 0 находим
х = пn; из уравнения sin x = 1 находим 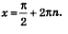 Но включить обе серии решений в ответ нельзя. Дело в том, что при значениях Но включить обе серии решений в ответ нельзя. Дело в том, что при значениях 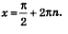 входящий в заданное уравнение множитель tg х не имеет смысла, т.е. значения входящий в заданное уравнение множитель tg х не имеет смысла, т.е. значения
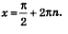 не принадлежат области определения уравнения (области допустимых значений уравнения — ОДЗ), это — посторонние корни. не принадлежат области определения уравнения (области допустимых значений уравнения — ОДЗ), это — посторонние корни.
3. Однородные тригонометрические уравнения
Здесь мы познакомимся с довольно часто встречающимися на практике тригонометрическими уравнениями специального вида.
Определение. Уравнение вида: 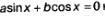 называют однородным тригонометрическим уравнением первой степени; уравнение вида: называют однородным тригонометрическим уравнением первой степени; уравнение вида: 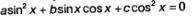 называют однородным тригонометрическим уравнением второй степени. называют однородным тригонометрическим уравнением второй степени.
Сначала поговорим о решении однородных тригонометрических уравнений первой степени, причем рассмотрим только самый общий случай, когда оба коэффициента а и Ъ отличны от нуля, так как, если а =0, уравнение принимает вид 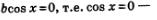 такое уравнение отдельного обсуждения не заслуживает; аналогично при Ь=0 получаем sin х =0, что тоже не требует отдельного обсуждения. такое уравнение отдельного обсуждения не заслуживает; аналогично при Ь=0 получаем sin х =0, что тоже не требует отдельного обсуждения.
Итак, дано уравнение 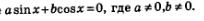 Разделив обе части уравнения почленно на соs x, получим: Разделив обе части уравнения почленно на соs x, получим:
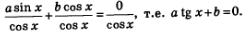
В итоге приходим к простейшему тригонометрическому уравнению
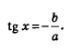
Внимание! Вообще-то делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя). Уверены ли мы, что в нашем уравнении соз х отличен от нуля? Давайте проанализируем. Предположим, что соз х =0. Тогда однородное уравнение а sin х+Ь соз х=0 примет вида зтдг=0, т.е. зщх=0 (вы ведь не забыли, что коэффициент а отличен от нуля). Получается, что и соз х=0, и зш л: =0, а это невозможно, так как зтх и соззс обращаются в нуль в различных точках. Итак, в однородном тригонометрическом уравнении первой степени деление обеих частей уравнения насозх— вполне благополучная операция.
Уравнения вида а зт тх+Ь соз тх=0 тоже называют однородными тригонометрическими уравнениями первой степени. Для их решения обе части уравнения делят почленно на соз тх.
Пример 7. Решить уравнение 2 sin х-3соз х=0.
Решение. Разделив обе части уравнения почленно на соз х, получим:
95
3 3
21§лс-3=0, л: = —, лс = агс 1%- + пп.
2 2
3
Ответ: х = агс1е- + пп.
2
Пример 8. Решить уравнение 8т2лс + со82лс =0.
Решение. Разделив обе части уравнения почленно насо82лс, получим: 182*+ 1=0, 1&2х=-1, 2х = агс1ё(-1)+ пп,
„л п пп
2х = — + пп, х = — + —.
4 8 2
^ п пп
Ответ: х ----1--.
8 2_^
Рассмотрим теперь однородное тригонометрическое уравнение второй степени:
а 81П2 х+Ь 81П x соз Х+С соз2 X =0.
Если коэффициент а отличен от нуля, т.е. в уравнении содержится член зт2 х с каким-то коэффициентом, отличным от нуля, то, рассуждая как и выше, нетрудно убедиться в том, что при интересующих нас значениях переменной сое хне обращается в нуль, а потому можно обе части уравнения разделить почленно на сое2 х. Что это даст? Смотрите:
а 81п2 X Ь 81п X соз X С соз2 X 0
сов2 X соз2 X сов2 X соз2 X
т.е. а 1§2х+Ь х+с =0.
Это — квадратное уравнение относительно новой переменной г = 1%х.
Пусть теперь в однородном тригонометрическом уравнении
а 81п2 Х + Ь 81п X соз Х + С соз2 X =0
коэффициент а равен 0, т.е. отсутствует член азт2 х. Тогда уравнение принимает вид:
Ь 81п X соз х + ссоз2 Х = 0.
Это уравнение можно решить методом разложения на множители: с08 X (Ъ 81п Х + С соз X) =0, соз X = 0 или Ъ 81п Х + С соз X =0.
Получились два уравнения, которые мы с вами решать умеем. Аналогично обстоит дело и в случае, когдас =0, т.е. когда однородное уравнение имеет вид а зт2 х+Ь зт х соз х=0 (здесь можно вынести за скобки зтх).
Фактически мы выработали
96
АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ автгх+Ь 81П хсоз х+ссоа2 х=0:
1. Посмотреть, есть ли в уравнении член азт2 х.
2. Если членавт2 хв уравнении содержится (т.е. а Ф 0), то уравнение решается делением обеих его частей на сое2 х и последующим введением новой переменной г = х.
3. Если член азт2 х в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят совх.
Так же обстоит дело и в однородных уравнениях вида: а 81П2 тх+Ъ 8111 тхсовтх+с сов2 тх=0.
Пример 9. Решить уравнение
81П2 лс - 3 81П л: соз х+ 2 сое2 х = 0.
Решение. Разделив обе част^ уравнения почленно на соз2 х, получим 1^х-31§ х + 2=0. Введя новую переменную г=Щх, получим г2 -Зг + 2=0, откуда находим г1 = 1, г2 =2. Значит, либо {%х = 1, либо 1%х=2. Из первого уравнения находим:
х = агс1ё 1 + пп, т.е. х = — + пп.
Из второго уравнения находим: х = агс1§ 2 + пп. п
Ответ: х = — + пп\ х = агс1§ 2 + пп. 4
Пример 10. Решить уравнение
•у/Ззтлссовлс + соз2 х=0.
Решение. Здесь отсутствует член вида а зш2 х, значит, делить обе части уравнения на соз2 х нельзя. Решим уравнение методом разложения на множители. Имеем:
совх(4з 8Н1л; + со8л;)=0, т.е. соз х = 0 или 73 зш х + соз х=0.
тт я
Из первого уравнения находим х = — + кп.
Второе уравнение — однородное тригонометрическое уравнение первой степени. Решим его с помощью почленного деления обеих частей уравнения насозлс:
81пя; + Со8я;=0,
4З^х + 1=0;
-П п
—Г= + пп,х = — + пп. л/3 6
1е л: = —Дг, откуда х = агс1§
4з
Ответ: х = — + пп: х = -—+пп. 2 6
В заключение рассмотрим более сложный пример.
4 Мордкович «Алгебра, 10 кл.»
97
Пример 11. Решить уравнение
3 81 п2 Зле - 2л/3 81Г1 Зх сое Зле + 5 сое2 Зле = 2 и выделить те его корни, которые принадлежат интервалу (-л, л).
Решение. Чем это уравнение сложнее предыдущих? Во-первых, оно не является однородным, так как в правой его части содержится не 0, а 2. Во-вторых, в левой части уравнения под знаками синуса и косинуса находится не х, а Зле. В-третьих, нужно не только решить уравнение в общем виде, но и выбрать корни, принадлежащие заданному промежутку. Эти три дополнительные трудности мы сейчас и начнем преодолевать.
С числом 2, содержащимся в правой части уравнения, мы поступим следующим образом. Известно, что зт21 + сое21 = 1 — это тождество верно для любого I. В частности, зт2 3* + сое2 Зле = 1. Но тогда 2 зт2 Зх + 2соз2 Зх =2. Заменив в правой части уравнения 2 на 2 81п2 Зле + 2со82 Зле, получим:
3 зт2 Зх - 273 зт Зх соа Зх + 5 соз2 Зх=2зт2Зх + 2 сов2 Зх.
Далее имеем:
3 зт2 Зх -2-Уз зт Зх соз Зх + 5сое2 3*'-2 зт2 Зх-2сов2 Зле = О, зт2 Зх-2^3 зт Зх соз Зле + Зсоз2 Зле =0.
Как видите, нам удалось преобразовать заданное уравнение в однородное тригонометрическое уравнение второй степени. Оно содержит в своем составе член зт2 Зх, значит, применив способ почленного деления на соз2 Зле, получим:
1§2 3 лс - 2-У31§ Зле + 3=0.
Положив г Зх, получим квадратное уравнение:
г2 -2л/3г +3=0.
Для решения этого уравнения можно использовать формулу корней квадратного уравнения, но изящнее сделать так: заметив, что
г2 -273г+3=(г-73)2, преобразовать квадратное уравнение к виду:
(г-7з)2=0,
и далее г--Уз =0.
Значит, 2 = л/5, т.е.
1§ЗХ = ТЗ, Зх = ап*8 -Уз + пп,
о 71
Злс = — + пп, 3
л пп
лс = - +-.
9 3
Осталось из найденной серии решений выбрать те корни уравнения, которые принадлежат заданному интервалу (-л, л). Можно осуществить «перебор по параметру», т.е. последовательно придать параметру п значения 0,1, 2,..., -1, -2,..., как мы это делали в п. 1 (примеры 2 иЗ). Но мы хотим показать вам еще один прием (быть может, он покажется вам более интересным).
98
Нам нужно найти такие значения х, которые содержатся в интервале (-л, л), т.е. удовлетворяют двойному неравенству -%<х<к. Поскольку л лл
х =— + —, получаем неравенство:
П ПП -л< —+-< л.
9 3
Умножив все части этого неравенства на 9 и разделив на тс, получим:
-9<1 + Зл<9, -10<3я<8,
10 8
--<п <-.
3 3
Осталось выяснить, какие целочисленные значения параметра п удовлетворяют последнему неравенству. Это значения: -3, -2, -1, 0,1, 2. Значит, если перечисленные шесть значений подставить вместо п в форте тел
мулу решении х = — н--, то мы тем самым и выделим интересующие нас
9 3
корни уравнения, принадлежащие заданному интервалу (-тс, тс). Итак:
1) если л = -3, то из формулы х=— + — получаем
9 3
п 8л
х =--л=--;
9 9
2) если л = -2, то из формулы х = — + — получаем
9 3
л _ 2л __ 5 л
3) если л = -1, то из формулы х + ^ получаем
_ л _ л _ 2 л
4) если л = 0, то из формулы + ~ получаем
л „ л
х=- + 0=~; 9 9
С\ 1 Я тел
5) если л = I, то из формулы х=—л--получаем
9 3 _ л я_4тс. *"9 + 3~~9~'
6) если л = 2, то из формулы х=— + — получаем
9 3
п 2тс 7тс
х=- +-=-.
9 3 9
^ 8л 5 л 2 л п 4тс 7п
Ответ:--;--;--; —; —.
9 9 9 9 9 9
4 й
99
А.Г. Мордкович Алгебра 10 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|