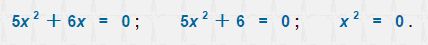|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Формулы корней квадратных уравнений Квадратные уравнения
Определение квадратного уравненияИз курса математики предыдущих классов вам уже известно, что такое уравнение, а вот какие же уравнения принято называть квадратными, нам еще предстоит разобраться. Если вы слышите такое словосочетание, как «квадратное уравнение», то ключевым словом в этой терминологии является слово «квадратное». Ну а теперь давайте более подробно рассмотрим, как должно выглядеть квадратное уравнение. А раз оно «квадратное», значит, такое уравнение непременно должно содержать икс в квадрате, также может быть икс в первой степени и простое число. Если говорить более простым языком, то в таком уравнении должен присутствовать икс, но его степень не должна быть больше двойки. Но, а если говорить языком математики, то это такое уравнение, которое выглядит так: ax2 + bx + c = 0, где a, b, c — какие-нибудь числа (a ≠ 0), x — неизвестное. Числа, которые имеются в квадратном уравнении, называются коэффициентами этого квадратного уравнения: • a – является первым коэффициентом квадратного уравнения; В целом, если рассматривать квадратное уравнение, которое имеет вид: ax2 + bx + c = 0 То можно увидеть, что в данное квадратное уравнение с его левой стороны имеет полный набор членов, где присутствует икс в квадрате с коэффициентом a, также икс в первой степени с коэффициентом b, ну и свободный член c. Квадратные уравнения со всеми тремя слагаемыми называются полными. Они имеют такой вид: Но если, к примеру, взять коэффициент b, который равен 0, то получается, что у нас пропадает икс в первой степени. Или же c равняется нулю, то тогда наше уравнение остается без свободного члена. Из выше сказанного делаем вывод, что перед нами квадратное уравнение, где нету коэффициента или свободного члена. Такие квадратные уравнения, у которых чего-то не достает, принято называть неполными квадратными уравнениями. Так, уравнения с нулевым коэффициентом b или c будут неполными квадратными уравнениями следующего вида, например: Если же в квадратном уравнении старший коэффициент равняется единице, то такое уравнение носит название приведенного квадратного уравнения. Способы решения квадратных уравненийЗачем уметь решать квадратные уравненияНа протяжении изучения всего курса алгебры в школе, изучению уравнений отводится больше часов, чем на какие-либо другие темы по математике. А задумывались ли вы, почему так? Просто, умение решать уравнения имеет не только огромное значение для досконального знания математики и естественных законов, но эти знания пригодятся вам и в практических целях. Ведь в повседневном реальном мире придется сталкиваться с различными проблемами, где никак не обойтись без решения различных видов уравнений. Обучившись их решать и овладев их способами решения, в дальнейшем вы сможете легко найти ответы в любой области науки и техники. А умение понимать и решать квадратные уравнения, является фундаментом к освоению знаний математических наук. История возникновения и развития квадратных уравненийПотребность в умении решать уравнения возникла еще в глубокой древности, при этом уже тогда люди вычисляли уравнения не только 1-й степени, но и 2-й. Это было продиктовано потребностью человека научиться вычислять площади земельных участков, а также делать шаги в сторону развития таких наук, как астрономия, физика, математика и т.д. Первыми умельцами в разрешении квадратных уравнений можно назвать жителей Вавилона. Они их научились решать еще 4000 лет до н.э. Естественно, что правила решения квадратных уравнений в вавилонских текстах далеко отличались от современных, но по существу они близки. В вавилонских трактатах не было понятия отрицательного числа, да и общие методы их решения кардинально отличались. Также пользовался решением квадратных уравнений и древнеиндийский математик Баудхаяма. В Европе первые формулы решения этих уравнений появились лишь в 1202 г. . Они были описаны итальянским математиком Леонардом Фибоначчи в его знаменитой книге «Книге абака». Немного позднее изучением этого важного математического вопроса с квадратными уравнениями занялись и такие ученые, как Ньютон, Франсуа Виет, Рене Декарт и другие известные математики. Применение квадратных уравнений в современной жизниИ если древний человек уже тогда применял для решения жизненных вопросов квадратные уравнения, то через столько лет изучения этого вопроса, их значение нисколько не уменьшилось, а даже наоборот увеличилось. Давайте с вами поразмыслим, где же теперь нашли применение квадратные уравнения, если не брать во внимание их изучение в школах и различных ВУЗах. Изучая тему квадратных уравнений, мы как-то не задумывались о том, что квадратные уравнения имеют широкое практическое применение. Без квадратных уравнений не обойтись при различных расчетах. Их можно использовать при строительстве, чтобы выяснить траекторию движения планет, в самолетостроении. Важны арифметические расчеты и в спорте. Домашнее задание: |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: