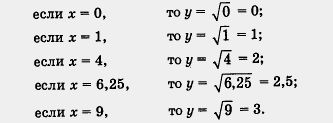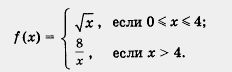|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = √х , ее свойства и график
Функция у = √х , ее свойства и график
Для построения графика функции 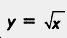 дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение  не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак: не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:
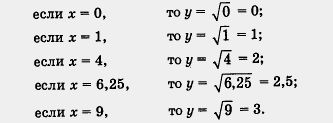
Итак, мы составили таблицу значений функции:
x
| 0
| 1
| 4
| 6,25
| 9
|
y
| 0
| 1
| 2
| 2,5
| 3
|
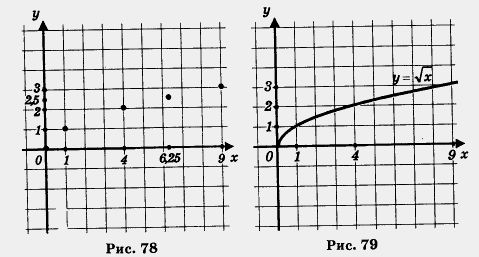
Построим найденные точки (0; 0), (1;1), (4; 2), (6,25; 2,5), (0;3) на координатной плоскости (рис. 78). Они располагаются некоторой линии, начертим ее (рис. 79). Получили график функции  . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции  , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо. , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
Свойства функции 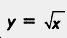
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (рис. 79).
1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; у > 0 при х > 0.
3. Функция возрастает на луче [0, + оо).
4. Функция ограничена снизу, но не ограничена сверху.
5. унаим. = 0 (достигается при х = 0), унаи6 не существует.
6. Функция непрерывна на луче [0, +оо).
Комментариев требует лишь свойство 4. Почему мы считаем, что функция не ограничена сверху? Возьмем, например, число 10. Найдется ли такое значение х, для которого будет выполнено неравенство  > 10? Конечно, достаточно взять х = 121, ведь > 10? Конечно, достаточно взять х = 121, ведь 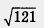 = 11, а 11 > 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство = 11, а 11 > 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство  > 40? Конечно, достаточно взять х = 2500, ведь > 40? Конечно, достаточно взять х = 2500, ведь 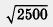 = 50, а 50 > 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство = 50, а 50 > 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство  > m (достаточно взять х = (m + 1)2; подумайте, почему это так). > m (достаточно взять х = (m + 1)2; подумайте, почему это так).
А теперь обратим внимание на одно любопытное обстоятельство. Рассмотрим две функции: у =  (ее график изображен на рис. 79) и у = х2, где х> 0 (ее график изображен на рис. 80). Мы только что перечислили шесть свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково. Они обнаружили принципиальные различия в характере графиков, заметив, что график функции (ее график изображен на рис. 79) и у = х2, где х> 0 (ее график изображен на рис. 80). Мы только что перечислили шесть свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково. Они обнаружили принципиальные различия в характере графиков, заметив, что график функции 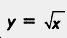 обращен выпуклостью вверх, тогда как обращен выпуклостью вверх, тогда как
график функции у = х2, где х > 0, обращен выпуклостью вниз.
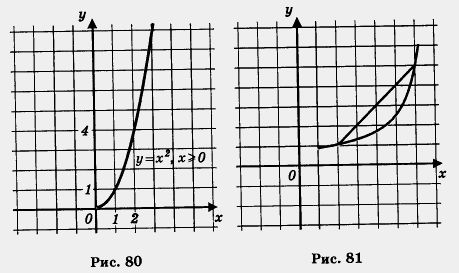
Обычно говорят, что функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 81); функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка (рис. 82).
Свойство выпуклости будем в дальнейшем включать в процедуру чтения графика.
Функция у = f (х)у где f (х) = , принимает любые неотрицательные значения. В самом деле, какое бы конкретное значение у > 0 ни задать, всегда найдется такое х, что выполняется равенство f (х) = у, т.е. , принимает любые неотрицательные значения. В самом деле, какое бы конкретное значение у > 0 ни задать, всегда найдется такое х, что выполняется равенство f (х) = у, т.е.  = у; для этого достаточно положить х = у2. Множество всех значений функции называют обычно областью значений функции. Для функции у = = у; для этого достаточно положить х = у2. Множество всех значений функции называют обычно областью значений функции. Для функции у = областью значения значений является луч [0, + оо). Это, кстати, хорошо читается по графику функции (рис. 79). Если спроецировать график на ось у, как раз и получится луч [0, + оо ). областью значения значений является луч [0, + оо). Это, кстати, хорошо читается по графику функции (рис. 79). Если спроецировать график на ось у, как раз и получится луч [0, + оо ).
Пример 1. Найти наименьшее и наибольшее значения функции у =  на отрезке: на отрезке:
а) [0, 4]; б) [1, 5].
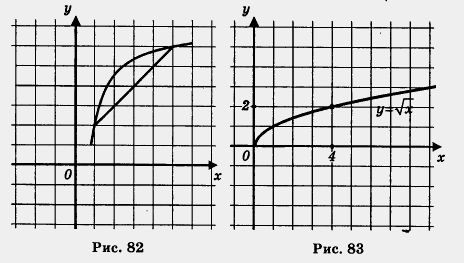
Решение, а) Построим график функции у =  и выделим его часть на отрезке [0, 4] (рис. 83). Замечаем, что Унаим. = 0 (достигается при х = 0), а унаи6 = 2 (достигается при х = 4). и выделим его часть на отрезке [0, 4] (рис. 83). Замечаем, что Унаим. = 0 (достигается при х = 0), а унаи6 = 2 (достигается при х = 4).
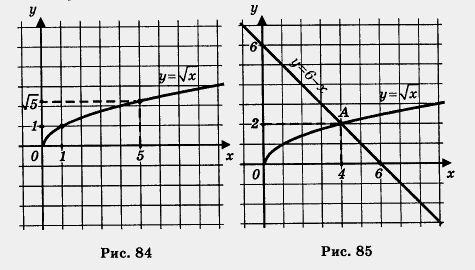
б) Построим график функции у =  и выделим его часть на отрезке [1, 5] (рис. 84). Замечаем, что унаим = 1 (достигается при х = 1), а унаиб = и выделим его часть на отрезке [1, 5] (рис. 84). Замечаем, что унаим = 1 (достигается при х = 1), а унаиб = 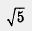 (достигается при х = 5). (достигается при х = 5).
О т в е т: а) унаим. = 0; унаиб = 2; б) унаим. = 1; ушиб = 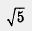
Пример 2. Решить уравнение  = 6 - х. = 6 - х.
Решение.
1) Рассмотрим две функции у = 6 - x и y = 
2) Построим график функции у =  (рис. 85). (рис. 85).
3) Построим график линейной функции у = 6 - х.
Это — прямая, которую можно построить по двум точкам (0; 6) и (6; 0). Прямая изображена на том же чертеже (рис. 85).
4) По чертежу устанавливаем, что графики пересекаются в одной точке А (4; 2). Так ли это на самом деле? Проверим: пара (4; 2) удовлетворяет и уравнению у =  и уравнению у = 6 - х. и уравнению у = 6 - х.
Это значит, что точка (4; 2) на самом деле служит точкой пересечения построенных графиков. Заданное уравнение имеет один корень 4 — это абсцисса точки А.
Ответ: 4.
Пример 3. Построить график функции 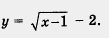
Решение. 1) Перейдем к вспомогательной системе координат с началом в точке (1; -2) (пунктирные прямые х = 1 и у = - 2 на рис. 86).
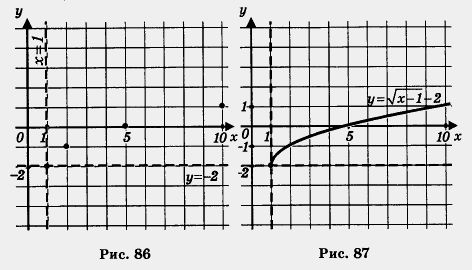
2) Привяжем функцию у =  к новой системе координат. к новой системе координат.
Для этого выберем контрольные точки для функции у =  . , например (0; 0), (1; 1), (4; 2), (9; 3), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 86). Построим ветвь параболы, проходящую через выбранные точки, — это и есть требуемый график (рис. 87). . , например (0; 0), (1; 1), (4; 2), (9; 3), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 86). Построим ветвь параболы, проходящую через выбранные точки, — это и есть требуемый график (рис. 87).
Пример 4. Построить и прочитать график функции y = - 
Решение. Выше, в § 8, мы заметили, что график функции у = - f (х) получается из графика функции у = f (x) с помощью преобразования симметрии относительно оси х.
Воспользовавшись этим, построим график функции у =  и отобразим его симметрично относительно оси х (рис. 88). Это и будет график функции у = - и отобразим его симметрично относительно оси х (рис. 88). Это и будет график функции у = -  . .
Перечислим свойства функции у = -  (по графику): (по графику):
1. Область определения функции — луч [0, + оо).
2. у = 0 при х = 0; у < 0 при х > 0.
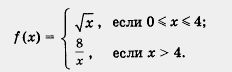
3. Функция убывает на луче [0, + оо).
4. Функция ограничена сверху и не ограничена снизу.
5 Унаиб. = 0 (достигается при х = 0), унаим не существует.
6. Функция непрерывна на луче [0, + од).
7. Область значений функции — луч (- оо, 0].
8. Функция выпукла вниз.
Пример 5. Построить и прочитать график функции y =f(x), где
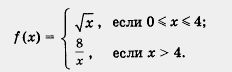
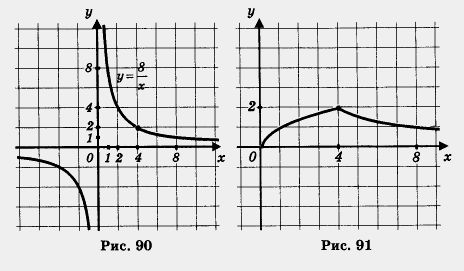
Решение. Сначала построим график функции у =  и выделим его часть на отрезке [0, 4] (рис. 89). Затем построим гиперболу и выделим его часть на отрезке [0, 4] (рис. 89). Затем построим гиперболу 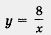 и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91). и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91).
Перечислим свойства функции у — f(x), т.е. прочитаем график.
1. Область определения функции — луч [0, + °о).
2. у = 0 при x = 0; у > 0 при х > 0.
3. Функция возрастает на отрезке [0, 4] и убывает на луче [4, + оо).
4. Функция ограничена и снизу и сверху.
5 Унаим. = 0 (достигается при х = 0); унаи6 = 2 (достигается при х = 4).
6. Функция непрерывна в заданной области определения.
7. Область значений функции — отрезок [0, 2].
8. Функция выпукла вверх на отрезке [0, 4] и выпукла вниз на луче [4, + оо).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|