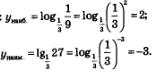|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Функция у = logaх, ее свойства и график
Функция у = logaх, ее свойства и график
В § 48 мы ввели понятие логарифма положительного числа по положительному и отличному от 1 основанию а. Для любого положительного числа можно найти логарифм по заданному основанию. Но тогда следует подумать и о функции вида 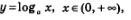 , о ее графике и свойствах. Этим и займемся в настоящем параграфе. , о ее графике и свойствах. Этим и займемся в настоящем параграфе.
Рассмотрим одновременно две функции: показательную у=ах и логарифмическую у =logaх. Пусть точка (b; с) принадлежит графику функции у=ах; это значит, что справедливо равенство с=аb. Перепишем это равенство «на языке логарифмов»: b = logа с. Последнее равенство означает, что точка (с; Ь) принадлежит графику функции у=logaх.
Итак, если точка (b; с) принадлежит графику функции у=ах, то точка (с;b) принадлежит графику функции у =logaх.
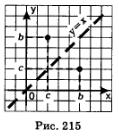
В § 40 мы доказали теорему о том, что точки координатной плоскости хОу с координатами (Ь; с) и (с; b) симметричны относительно прямой у = х (рис. 215). Таким образом, справедливо следующее утверждение:
График функции у = logа х симметричен графику функции у =ах относительно прямой у -х.
На рис. 216 схематически изображены графики функций у=ах и у=logах случае, когда а >1; на рис. 217 схематически изображены графики функций у—ах и у=logаx в случае, когда 0 <а <1.
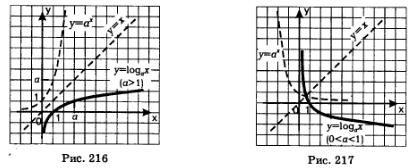
График функции у=logaх называют логарифмической кривой, хотя на самом деле нового названия можно было не придумывать. Ведь это та же экспонента, что служит графиком показательной функции, только по-другому расположенная в координатной плоскости.
Если значение основания а указано, то график логарифмической функции можно построить по точкам. Пусть, например, нужно построить график функции у=logaх. Составляя таблицу контрольных точек, будем руководствоваться соотношением 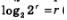 (см. § 48). Поэтому в таблицу в качестве значений аргумента х мы включим числа, являющиеся степенями числа 2. (см. § 48). Поэтому в таблицу в качестве значений аргумента х мы включим числа, являющиеся степенями числа 2.
Имеем:
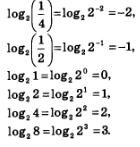
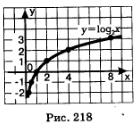
Построив на координатной плоскости точки
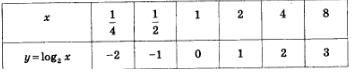
проводим через них логарифмическую кривую (рис. 218).
Свойства функции 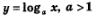
Необходимую информацию извлекаем из геометрической модели, представленной на рис. 216.
1) 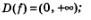
2) не является ни четной, ни нечетной',
3) возрастает на 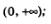
4) не ограничена сверху, не ограничена снизу;
5) не имеет ни наибольшего, ни наименьшего значений;
6) непрерывна;

7)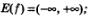
8) выпукла вверх.
Сравните график функции у = logах, изображенный на рис. 216, и график функции у = aг(0 < r < 1), изображенный на рис. 187 (в § 44). Не правда ли, они похожи (при х > о)? На самом деле между ними есть принципиальная разница: график функции у = х' «набирает обороты» быстрее. Иными словами, для достаточно больших значений х ордината графика степенной функции у = хг (при 0 < г < 1 и уж тем более при г 1) значительно больше соответствующей ординаты графика логарифмической функции с любым основанием, большим, чем 1. В курсе математического анализа доказано, что при о >1 и г> 0 выполняется равенство
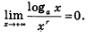
Свойства функции у = logaх, О < а < 1
Необходимую информацию извлекаем из геометрической модели, представленной на рис. 217.
1)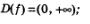
2) не является ни четной, ни нечетной;
3) убывает на 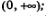
4) не ограничена сверху, не ограничена снизу;
5) нет ни наибольшего, ни наименьшего значений;
6) непрерывна;
7)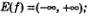
8) выпукла вниз.
Отметим, что ось у является вертикальной асимптотой графика логарифмической функции и в случае, когда о > 1, и в случае, когда О <а <1.
Прежде чем переходить к решению примеров, заметим, что логарифмическая функция, как и показательная, существенно отличается от всех функций, которые вы изучали в курсе алгебры 7—9-го классов. Поэтому есть смысл повторить сказанное в § 45: чтобы основательно изучить новый объект, надо рассмотреть его с разных сторон, в разных ситуациях, поэтому примеров будет много.
Пример 1. Найти наименьшее и наибольшее значения функций на заданном промежутке:
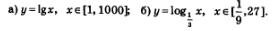
Решение, а) Функция у = lgх — непрерывная и возрастающая, поскольку основание этой логарифмической функции больше 1 (вы, конечно, помните, что 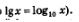 Следовательно, своих наименьшего и наибольшего значений функция достигает на концах заданного отрезка [1,1000]. Следовательно, своих наименьшего и наибольшего значений функция достигает на концах заданного отрезка [1,1000].
Имеем:
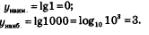
б) Функция 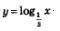 — непрерывная и убывающая, поскольку основание этой логарифмической функции, т.е. число — непрерывная и убывающая, поскольку основание этой логарифмической функции, т.е. число 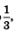 , меньше 1. Следовательно, своих наибольшего и наименьшего значений функция достигает на концах заданного отрезка , меньше 1. Следовательно, своих наибольшего и наименьшего значений функция достигает на концах заданного отрезка 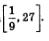
Имеем:
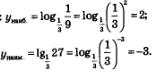
Пример 2. Решить уравнение и неравенства:
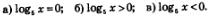
Решение. График функции у=logaх схематически изображен на рис. 216. Заданные уравнение и неравенства нетрудно решить, используя эту геометрическую модель.
а) Уравнение loga х=0 имеет один корень x = 1, поскольку график функции у = logaх пересекает ось х в единственной точке (1; 0).
б) График функции у = logax расположен выше оси х при x > 1. Значит, решение неравенства logaх > 0 имеет вид х >1. .
в) График функции у = logaх расположен ниже оси х при 0 < х < 1. Значит, решение неравенства logax < 0 имеет вид 0 < х < 1.
Ответ: а)х = 1; б) х>1; в) 0<x<1.
Пример 3. Решить уравнение и неравенства:
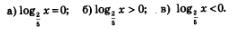
Решение. График функции 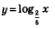 схематически изображен на рис. 217. Заданные уравнение и неравенства нетрудно решить, используя эту геометрическую модель. схематически изображен на рис. 217. Заданные уравнение и неравенства нетрудно решить, используя эту геометрическую модель.
а) Уравнение 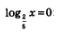 имеет один корень имеет один корень 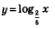 , поскольку график функции , поскольку график функции 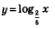 пересекает ось х в единственной точке (1; 0). пересекает ось х в единственной точке (1; 0).
б) График функции 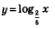 расположен выше оси у при 0<х<1. Значит, решение неравенства расположен выше оси у при 0<х<1. Значит, решение неравенства 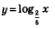 >0 имеет вид 0<х<1. >0 имеет вид 0<х<1.
в) График функции 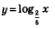 расположен ниже оси х при х > 1. Значит, решение неравенства расположен ниже оси х при х > 1. Значит, решение неравенства 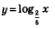 <0 имеет вид х > 1. <0 имеет вид х > 1.
Ответ: а) x = 1; б) 0x<1; в) x>1.
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|