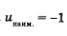|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Функция y = sinx, ee свойства и график
Функция y = sinx, ee свойства и график
Функция у = sin X.
Выше, в § 20, мы сформулировали правило, позволяющее каждому числу t поставить в соответствие число cos t, т.е. охарактеризовали функция y = sin t. Отметим некоторые ее свойства.
Свойства функции u = sin t.
Свойство 1. Область определения — множество К действительных чисел.
Это следует из того, что любому числу 2 соответствует на числовой окружности точка М(1), которая имеет вполне определенную ординату; эта ордината и есть cos t.
Свойство 2. u = sin t — нечетная функция.
Это следует из того, что, как было доказано в § 19, для любого t выполняется равенство 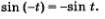
Значит, график функции и = sin t, как график любой нечетной функции, симметричен относительно начала координат в прямоугольной системе координат tOи.
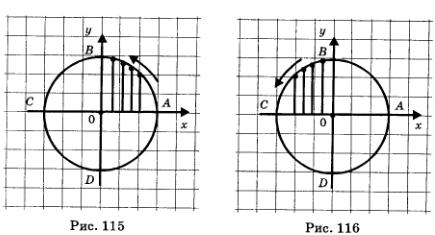
Свойство 3. Функция u = sin t возрастает на отрезке 
Это следует из того, что при движении точки по первой четверти числовой окружности 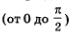 ордината постепенно увеличивается (от 0 до 1 — см. рис. 115), а при движении точки по второй четверти числовой окружности ордината постепенно увеличивается (от 0 до 1 — см. рис. 115), а при движении точки по второй четверти числовой окружности 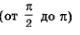 ордината постепенно уменьшается (от 1 до 0 — см. рис. 116). ордината постепенно уменьшается (от 1 до 0 — см. рис. 116).
Свойство 4. Функция u = sin t ограничена и снизу, и сверху. Это следует из того, что, как мы видели в § 19, для любого t справедливо неравенство
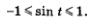
Свойство 5. 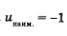 (этого значения функция достигает в любои точке вида (этого значения функция достигает в любои точке вида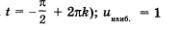 (этого значения функция достигает в любой точке вида (этого значения функция достигает в любой точке вида 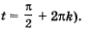
Воспользовавшись полученными свойствами, построим график интересующей нас функции. Но (внимание!) вместо u — sin t будем писать у = sin x (ведь нам привычнее запись у = f(х), а не u = f(t)). Значит, и строить график будем в привычной системе координат хОу (а не tOy).
Составим таблицу значений функции у — sin х:
Замечание. Приведем одну из версий происхождения термина «синус». По-латыни sinus означает изгиб (тетива лука). Построенный график в какой-то степени оправдывает эту терминологию.
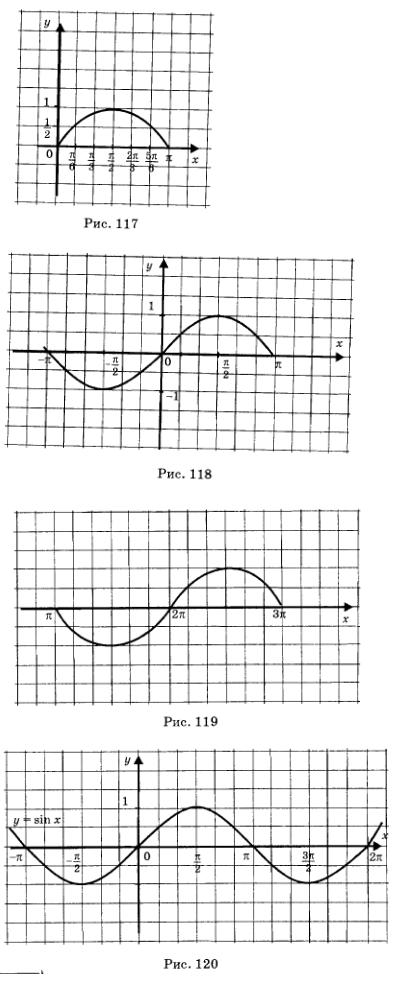
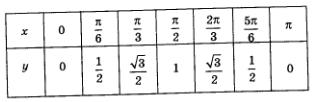
Линию, служащую графиком функции у = sin х, называют синусоидой. Ту часть синусоиды, которая изображена на рис. 118 или 119, называют волной синусоиды, а ту часть синусоиды, которая изображена на рис. 117, называют полуволной или аркой синусоиды.
А.Г. Мордкович Алгебра 10 класс
Видеопо географии скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|