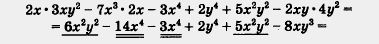|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Основные понятия</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Основные понятия, математическая модель, многочлены, одночлен</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Основные понятия''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Основные понятия''' |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | В главе 3 мы уже отмечали, что не любые одночлены можно складывать и вычитать, а только подобные; также отмечали и то, что реальная задача может привести к такой математической модели, в которой будет содержаться сумма неподобных одночленов. Для изучения таких сумм в математике введено по- <br>нятие многочлена. <br>''Определение.'' Многочленом называют сумму одночленов. <br>Примеры многочленов: <br>2а + b; bа<sup>4</sup> - ЗаЬ<sup>2</sup> - Заb<sup>2</sup> + 7с; х<sup>5</sup> + х<sup>4</sup> + x<sup>2</sup> - 2. <br>Разумеется, существуют алгебраические выражения, не являющиеся многочленами. Например, [[Image:08-06-1.jpg]]<br>Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена: если их два, то говорят, что дан двучлеи (например, 2а + b — двучлен), если их три, то говорят^ что дан трехчлен (например, 5а<sup>2</sup> - 2сb<sup>2</sup> + 7с — трехчлен). С этой точки зрения становится понятнее термин «одночлен» и <br>то, что одночлен обычно считают частным случаем многочлена (одночлен — это многочлен, в состав которого входит всего один член).
| + | ''' Основные понятия'''<br> |
| | | | |
| - | <u>Замечание 1.</u> Выше мы не раз проводили аналогию между обычным и математическим языком. В обычном языке — буквы, в математическом — числа, <br>переменные, степени; в обычном языке — слоги, в математическом — одночлены; в обычном языке — слова, в математическом — многочлены. Но разве нет в русском языке слов, состоящих из одного слога? <br>Сколько угодно: «ад», «рай», «юг», «ил» и т.п.; так и в математическом языке одночлен (слог) есть многочлен (слово), просто этот многочлен состоит из одно- <br>го члена.
| + | <br> |
| | | | |
| - | <u>Замечание 2.</u> Говорят, в Африке есть племя, считающее так: «один», «два», «три», «много». Наша терминология применительно к многочленам напоминает <br>африканскую: одночлен, двучлен, трехчлен, многочлен (обычно ни «четырехчлен», ни «пятичлен» не говорят). <br>Теперь подготовимся к восприятию серьезного понятия. <br>Рассмотрим многочлен
| + | В главе 3 мы уже отмечали, что не любые одночлены можно складывать и вычитать, а только подобные; также отмечали и то, что реальная задача может привести к такой '''[[Что такое математическая модель|математической модели]]''', в которой будет содержаться сумма неподобных одночленов. Для изучения таких сумм в математике введено понятие многочлена. <br> |
| | | | |
| - | [[Image:08-06-2.jpg]]<br><br>To, что это — многочлен, сомнению не подлежит (поскольку записана сумма одночленов), но нравится ли вам такая запись? <br>Наверное, нет. Почему?
| + | <br>''Определение.'' Многочленом называют сумму одночленов. <br> |
| | | | |
| - | <u>Во-первых</u>, одночлен 2ab<sup>2</sup> • 3a<sup>2</sup>b не записан в стандартном виде, а мы знаем, что стандартный вид — наиболее удобная запись одночлена. Приведя его к стандартному виду, получим: 6a<sup>3</sup>b<sup>3</sup>. <br>Аналогично надо привести к стандартному виду еще один член <br>многочлена, а именно: [[Image:08-06-3.jpg]] Получим: - 2a<sup>3</sup>b<sup>3</sup>. <br>Теперь запись данного многочлена принимает более приятный вид
| + | <br>Примеры многочленов: <br> |
| | | | |
| - | 6а<sup>3</sup>b<sup>3</sup> - 5а - 7a + Зb<sup>2</sup> - 2а<sup>3</sup>b<sup>3</sup> - 2b<sup>2</sup>. <br><u>Во-вторых</u>, поскольку от перемены мест слагаемых сумма не меняется, подобные одночлены можно расположить рядом, а затем сложить. Получим: <br>(6а<sup>3</sup>b<sup>3</sup> - 2а<sup>3</sup>b<sup>3</sup>) + (- 5а - 7а) + (Зb<sup>2</sup> - 2b<sup>2</sup>) = 4а<sup>3</sup>b<sup>3</sup> - 12а + b<sup>2</sup>. <br>Правда, обычно подобные одночлены в многочлене не переставляют, их одинаково подчеркивают, а потом складывают:
| + | 2а + b; bа<sup>4</sup> - ЗаЬ<sup>2</sup> - Заb<sup>2</sup> + 7с; х<sup>5</sup> + х<sup>4</sup> + x<sup>2</sup> - 2. <br> |
| | | | |
| - | [[Image:08-06-4.jpg]]<br>Эту процедуру называют приведением подобных членов многочлена. <br>Если в многочлене все члены записаны в стандартном виде и приведены подобные члены, то говорят, что многочлен приведен к стандартному виду (или записан в стандартном виде). <br>Теперь вы понимаете, почему запись 4а<sup>3</sup>b<sup>3</sup> - 12а + b<sup>2</sup> предпочтительнее первоначальной записи: <br>[[Image:08-06-5.jpg]]<br><br>Дело в том, что первоначальная запись — не стандартный вид многочлена, а 4а<sup>3</sup>b<sup>3</sup> - 12а + b<sup>2</sup> — стандартный вид. <br>Любой многочлен можно привести к стандартному виду. Условимся в дальнейшем всегда с этого начинать — так удобнее производить действия с <br>многочленами. <br>Обычно многочлен обозначают буквой р или Р — с этой буквы начинается греческое слово polys («многий», «многочисленный»; многочлены в математике <br>называют также полиномами). В обозначение включают и переменные, из которых состоят члены многочлена. Например, многочлен
| + | Разумеется, существуют алгебраические выражения, не являющиеся '''[[Розклад многочленів на множники. Винесення спільного множника за дужки. Задачі та вправи|многочленами]]'''. Например, <br> |
| | | | |
| - | 2х<sup>2</sup>- 5x + 3 обозначают рx) — читается: «пэ от икс»; многочлен 2х<sup>2</sup>+3ху - у<sup>4</sup> обозначают р(х, у) — читается: «пэ от икс, игрек» и т. д. <br>Пример. Дан многочлен | + | [[Image:08-06-1.jpg|120px|Алгебраические выражения]] |
| | + | |
| | + | <br>Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена: если их два, то говорят, что дан двучлеи (например, 2а + b — двучлен), если их три, то говорят^ что дан трехчлен (например, 5а<sup>2</sup> - 2сb<sup>2</sup> + 7с — трехчлен). С этой точки зрения становится понятнее термин «одночлен» и то, что одночлен обычно считают частным случаем многочлена (одночлен — это многочлен, в состав которого входит всего один член). |
| | + | |
| | + | <u>Замечание 1.</u> Выше мы не раз проводили аналогию между обычным и '''[[Что такое математический язык|математическим языком]]'''. В обычном языке — буквы, в математическом — числа, переменные, степени; в обычном языке — слоги, в математическом — одночлены; в обычном языке — слова, в математическом — многочлены. Но разве нет в русском языке слов, состоящих из одного слога? |
| | + | |
| | + | Сколько угодно: «ад», «рай», «юг», «ил» и т.п.; так и в математическом языке одночлен (слог) есть многочлен (слово), просто этот многочлен состоит из одного члена. |
| | + | |
| | + | <u>Замечание 2.</u> Говорят, в Африке есть племя, считающее так: «один», «два», «три», «много». Наша терминология применительно к многочленам напоминает африканскую: одночлен, двучлен, трехчлен, многочлен (обычно ни «четырехчлен», ни «пятичлен» не говорят). |
| | + | |
| | + | Теперь подготовимся к восприятию серьезного понятия. |
| | + | |
| | + | Рассмотрим многочлен |
| | + | |
| | + | [[Image:08-06-2.jpg|400px|Многочлен]]<br><br>To, что это — многочлен, сомнению не подлежит (поскольку записана сумма одночленов), но нравится ли вам такая запись? |
| | + | |
| | + | Наверное, нет. Почему? |
| | + | |
| | + | <u>Во-первых</u>, одночлен 2ab<sup>2</sup> • 3a<sup>2</sup>b не записан в стандартном виде, а мы знаем, что стандартный вид — наиболее удобная запись одночлена. Приведя его к стандартному виду, получим: 6a<sup>3</sup>b<sup>3</sup>. |
| | + | |
| | + | Аналогично надо привести к стандартному виду еще один член многочлена, а именно: [[Image:08-06-3.jpg|100px|Член многочлена]] Получим: - 2a<sup>3</sup>b<sup>3</sup>. |
| | + | |
| | + | Теперь запись данного многочлена принимает более приятный вид |
| | + | |
| | + | 6а<sup>3</sup>b<sup>3</sup> - 5а - 7a + Зb<sup>2</sup> - 2а<sup>3</sup>b<sup>3</sup> - 2b<sup>2</sup>. |
| | + | |
| | + | <u>Во-вторых</u>, поскольку от перемены мест слагаемых сумма не меняется, подобные одночлены можно расположить рядом, а затем сложить. Получим: |
| | + | |
| | + | (6а<sup>3</sup>b<sup>3</sup> - 2а<sup>3</sup>b<sup>3</sup>) + (- 5а - 7а) + (Зb<sup>2</sup> - 2b<sup>2</sup>) = 4а<sup>3</sup>b<sup>3</sup> - 12а + b<sup>2</sup>. |
| | + | |
| | + | Правда, обычно подобные '''[[Одночлен. Піднесення одночленів до степеня. Множення одночленів|одночлен]]''' в многочлене не переставляют, их одинаково подчеркивают, а потом складывают: |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:08-06-4.jpg|400px|Многочлен]] |
| | + | |
| | + | <br>Эту процедуру называют приведением подобных членов многочлена. <br>Если в многочлене все члены записаны в стандартном виде и приведены подобные члены, то говорят, что многочлен приведен к стандартному виду (или записан в стандартном виде). <br>Теперь вы понимаете, почему запись 4а<sup>3</sup>b<sup>3</sup> - 12а + b<sup>2</sup> предпочтительнее первоначальной записи: |
| | + | |
| | + | <br>[[Image:08-06-5.jpg|400px|Многочлен]]<br><br>Дело в том, что первоначальная запись — не стандартный вид многочлена, а 4а<sup>3</sup>b<sup>3</sup> - 12а + b<sup>2</sup> — стандартный вид. <br>Любой многочлен можно привести к стандартному виду. Условимся в дальнейшем всегда с этого начинать — так удобнее производить действия с многочленами. |
| | + | |
| | + | Обычно многочлен обозначают буквой р или Р — с этой буквы начинается греческое слово polys («многий», «многочисленный»; многочлены в математике называют также полиномами). В обозначение включают и переменные, из которых состоят члены многочлена. Например, многочлен 2х<sup>2</sup>- 5x + 3 обозначают рx) — читается: «пэ от икс»; многочлен 2х<sup>2</sup>+3ху - у<sup>4</sup> обозначают р(х, у) — читается: «пэ от икс, игрек» и т. д. |
| | + | |
| | + | <br>Пример. Дан многочлен |
| | | | |
| | р (х, у) = 2х- Зху<sup>2</sup> - 7х<sup>3</sup> • 2х - Зx<sup>4</sup> + 2у<sup>4</sup> + 5х<sup>2</sup>у<sup>2</sup> - 2ху • 4у<sup>2</sup>. | | р (х, у) = 2х- Зху<sup>2</sup> - 7х<sup>3</sup> • 2х - Зx<sup>4</sup> + 2у<sup>4</sup> + 5х<sup>2</sup>у<sup>2</sup> - 2ху • 4у<sup>2</sup>. |
| | | | |
| - | а) Записать его в стандартном виде; <br>б) вычислить: р ( 1, 2); р (- 1,1); р ( 0,1). | + | а) Записать его в стандартном виде; |
| | + | |
| | + | б) вычислить: р ( 1, 2); р (- 1,1); р ( 0,1). |
| | | | |
| | Р е ш е н и е. а) Имеем: | | Р е ш е н и е. а) Имеем: |
| | | | |
| - | [[Image:08-06-6.jpg]]<br>''' =11x<sup>2</sup>y<sup>2</sup>-17x<sup>4</sup>+2y<sup>4</sup>-8xy<sup>3</sup>'''<br>— стандартный вид многочлена. | + | <br> |
| | + | |
| | + | [[Image:08-06-6.jpg|480px|Многочлен]]<br>''' =11x<sup>2</sup>y<sup>2</sup>-17x<sup>4</sup>+2y<sup>4</sup>-8xy<sup>3</sup>'''<br>— стандартный вид многочлена. |
| | | | |
| | б) Запись р(1, 2) означает, что нужно найти значение многочлена р (х, у) при х = 1, у = 2. Вычисления будем производить для многочлена, записанного в стандартном виде: | | б) Запись р(1, 2) означает, что нужно найти значение многочлена р (х, у) при х = 1, у = 2. Вычисления будем производить для многочлена, записанного в стандартном виде: |
| Строка 39: |
Строка 85: |
| | Итак, (р1, 2) = -'5. | | Итак, (р1, 2) = -'5. |
| | | | |
| - | Аналогично p(-1,1)=11 • (-1)<sup>2</sup> •1<sup>2</sup>- 17•(-1)<sup>4</sup>+2•14-8•(-1)•1<sup>3</sup>= 11-17 + 2 + 8 = 4, <br>т. е. р(- 1,1) = 4. <br>Наконец, <br>р (0, 1)= 11 • О<sup>2</sup> • I<sup>2</sup> - 17 • О<sup>4</sup> + 2 • I<sup>4</sup> - 8 •( 1) • I3 = = 0-0 + 2-0 = 2. <br>Итак, р (0, 1)=2. <br><br> | + | Аналогично p(-1,1)=11 • (-1)<sup>2</sup> •1<sup>2</sup>- 17•(-1)<sup>4</sup>+2•14-8•(-1)•1<sup>3</sup>= 11-17 + 2 + 8 = 4, <br>т. е. р(- 1,1) = 4. <br>Наконец, <br>р (0, 1)= 11 • О<sup>2</sup> • I<sup>2</sup> - 17 • О<sup>4</sup> + 2 • I<sup>4</sup> - 8 •( 1) • I3 = = 0-0 + 2-0 = 2. |
| | + | |
| | + | Итак, р (0, 1)=2. <br><br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <sub>Планы конспектов уроков по математике 7 класса [[Математика|скачать]], учебники и книги бесплатно, разработки уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | <sub>Планы конспектов уроков по математике 7 класса [[Математика|скачать]], учебники и книги бесплатно,[http://xvatit.com/vuzi/ '''разработки уроков'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | + | |
| | + | <br> |
| | + | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 18:50, 14 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Основные понятия
Основные понятия
В главе 3 мы уже отмечали, что не любые одночлены можно складывать и вычитать, а только подобные; также отмечали и то, что реальная задача может привести к такой математической модели, в которой будет содержаться сумма неподобных одночленов. Для изучения таких сумм в математике введено понятие многочлена.
Определение. Многочленом называют сумму одночленов.
Примеры многочленов:
2а + b; bа4 - ЗаЬ2 - Заb2 + 7с; х5 + х4 + x2 - 2.
Разумеется, существуют алгебраические выражения, не являющиеся многочленами. Например,
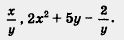
Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена: если их два, то говорят, что дан двучлеи (например, 2а + b — двучлен), если их три, то говорят^ что дан трехчлен (например, 5а2 - 2сb2 + 7с — трехчлен). С этой точки зрения становится понятнее термин «одночлен» и то, что одночлен обычно считают частным случаем многочлена (одночлен — это многочлен, в состав которого входит всего один член).
Замечание 1. Выше мы не раз проводили аналогию между обычным и математическим языком. В обычном языке — буквы, в математическом — числа, переменные, степени; в обычном языке — слоги, в математическом — одночлены; в обычном языке — слова, в математическом — многочлены. Но разве нет в русском языке слов, состоящих из одного слога?
Сколько угодно: «ад», «рай», «юг», «ил» и т.п.; так и в математическом языке одночлен (слог) есть многочлен (слово), просто этот многочлен состоит из одного члена.
Замечание 2. Говорят, в Африке есть племя, считающее так: «один», «два», «три», «много». Наша терминология применительно к многочленам напоминает африканскую: одночлен, двучлен, трехчлен, многочлен (обычно ни «четырехчлен», ни «пятичлен» не говорят).
Теперь подготовимся к восприятию серьезного понятия.
Рассмотрим многочлен
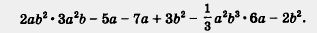
To, что это — многочлен, сомнению не подлежит (поскольку записана сумма одночленов), но нравится ли вам такая запись?
Наверное, нет. Почему?
Во-первых, одночлен 2ab2 • 3a2b не записан в стандартном виде, а мы знаем, что стандартный вид — наиболее удобная запись одночлена. Приведя его к стандартному виду, получим: 6a3b3.
Аналогично надо привести к стандартному виду еще один член многочлена, а именно: 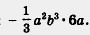 Получим: - 2a3b3. Получим: - 2a3b3.
Теперь запись данного многочлена принимает более приятный вид
6а3b3 - 5а - 7a + Зb2 - 2а3b3 - 2b2.
Во-вторых, поскольку от перемены мест слагаемых сумма не меняется, подобные одночлены можно расположить рядом, а затем сложить. Получим:
(6а3b3 - 2а3b3) + (- 5а - 7а) + (Зb2 - 2b2) = 4а3b3 - 12а + b2.
Правда, обычно подобные одночлен в многочлене не переставляют, их одинаково подчеркивают, а потом складывают:
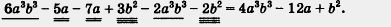
Эту процедуру называют приведением подобных членов многочлена.
Если в многочлене все члены записаны в стандартном виде и приведены подобные члены, то говорят, что многочлен приведен к стандартному виду (или записан в стандартном виде).
Теперь вы понимаете, почему запись 4а3b3 - 12а + b2 предпочтительнее первоначальной записи:
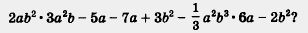
Дело в том, что первоначальная запись — не стандартный вид многочлена, а 4а3b3 - 12а + b2 — стандартный вид.
Любой многочлен можно привести к стандартному виду. Условимся в дальнейшем всегда с этого начинать — так удобнее производить действия с многочленами.
Обычно многочлен обозначают буквой р или Р — с этой буквы начинается греческое слово polys («многий», «многочисленный»; многочлены в математике называют также полиномами). В обозначение включают и переменные, из которых состоят члены многочлена. Например, многочлен 2х2- 5x + 3 обозначают рx) — читается: «пэ от икс»; многочлен 2х2+3ху - у4 обозначают р(х, у) — читается: «пэ от икс, игрек» и т. д.
Пример. Дан многочлен
р (х, у) = 2х- Зху2 - 7х3 • 2х - Зx4 + 2у4 + 5х2у2 - 2ху • 4у2.
а) Записать его в стандартном виде;
б) вычислить: р ( 1, 2); р (- 1,1); р ( 0,1).
Р е ш е н и е. а) Имеем:
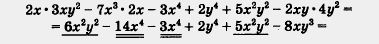
=11x2y2-17x4+2y4-8xy3
— стандартный вид многочлена.
б) Запись р(1, 2) означает, что нужно найти значение многочлена р (х, у) при х = 1, у = 2. Вычисления будем производить для многочлена, записанного в стандартном виде:
р(х, у) = 11x2y2 - 17x4 + 2у4 - 8ху3.
Имеем:
р( 1, 2) = 11 • I2 • 22 - 17 • I4 + 2 • 24 - 8 • 1 • 23= 44-17+ 32-64 = -5.
Итак, (р1, 2) = -'5.
Аналогично p(-1,1)=11 • (-1)2 •12- 17•(-1)4+2•14-8•(-1)•13= 11-17 + 2 + 8 = 4,
т. е. р(- 1,1) = 4.
Наконец,
р (0, 1)= 11 • О2 • I2 - 17 • О4 + 2 • I4 - 8 •( 1) • I3 = = 0-0 + 2-0 = 2.
Итак, р (0, 1)=2.
Планы конспектов уроков по математике 7 класса скачать, учебники и книги бесплатно,разработки уроков по математике онлайн
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|