|
|
|
| (4 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Что такое математическая модель </metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, математическая модель, математический язык, график, таблица, решение, уравнение</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Что такое математическая модель''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Что такое математическая модель''' |
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | ''' ЧТО ТАКОЕ МАТЕМАТИЧЕСКАЯ <br> МОДЕЛЬ''' | + | ''' Что такое математическая модель ''' |
| | | | |
| - | <br>Представьте себе такую ситуацию: в школе четыре седьмых класса. | + | <br>Представьте себе такую ситуацию: в [http://xvatit.com/vuzi/ '''школе'''] четыре седьмых класса. |
| | | | |
| | В 7А учатся 15 девочек и 13 мальчиков, <br> | | В 7А учатся 15 девочек и 13 мальчиков, <br> |
| Строка 19: |
Строка 19: |
| | в 7Г — 20 девочек и 10 мальчиков. | | в 7Г — 20 девочек и 10 мальчиков. |
| | | | |
| - | Если нам нужно ответить на вопрос, сколько учеников в каждом из седьмых классов, то нам 4 раза придется осуществлять одну и ту же операцию сложения: <br>в 7А 15 + 13 = 28 учеников; <br>в 7Б 12 +12 = 24 ученика; <br>в 7В 9 + 18 = 27 учеников; <br>в 7Г 20 + 10 = 30 учеников. | + | Если нам нужно ответить на вопрос, сколько учеников в каждом из седьмых классов, то нам 4 раза придется осуществлять одну и ту же операцию сложения: <br> |
| | | | |
| - | Используя математический язык, можно все эти четыре разные ситуации объединить: в классе учатся а девочек и Ь мальчиков, значит, всего учеников а + Ь. Эту запись а + Ь называют математической моделью данной реальной ситуации. Алгебра в основном занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.
| + | в 7А 15 + 13 = 28 учеников; <br>в 7Б 12 +12 = 24 ученика; <br>в 7В 9 + 18 = 27 учеников; <br>в 7Г 20 + 10 = 30 учеников. |
| | | | |
| - | В следующей таблице приведены различные реальные ситуации и их математические модели; при этом а — число девочек в <br>классе, 6 — число мальчиков в том же классе.
| + | Используя '''[[Что такое математический язык|математический язык]]''', можно все эти четыре разные ситуации объединить: в классе учатся а девочек и b мальчиков, значит, всего учеников а + b. Эту запись а + b называют математической моделью данной реальной ситуации. Алгебра в основном занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре. |
| | | | |
| - | {| cellspacing="1" cellpadding="1" border="1" style="width: 786px; height: 45px;" | + | В следующей '''[[Задачі до уроку: Що ти знаєш? Повторення вивченого у 3 класі. Табличне і поза табличне множення|таблице]]''' приведены различные реальные ситуации и их математические модели; при этом а — число девочек в классе, 6 — число мальчиков в том же классе. |
| | + | |
| | + | <br> |
| | + | |
| | + | {| cellspacing="1" cellpadding="1" border="1" style="width: 609px; height: 311px;" |
| | |- | | |- |
| - | | № | + | | № |
| - | | Реальная ситуация | + | | Реальная ситуация |
| - | | Математическая модель | + | | Математическая модель |
| | |- | | |- |
| - | | 1 | + | | 1 |
| - | | В классе девочек и мальчиков <br>поровну (как в 7Б) | + | | В классе девочек и мальчиков поровну (как в 7Б) |
| - | | a=b | + | | a = b |
| | |- | | |- |
| - | | 2 | + | | 2 |
| - | | Девочек на 2 больше, <br>чем мальчиков (как в 7А) | + | | Девочек на 2 больше, чем мальчиков (как в 7А) |
| - | | a-b = 2 <br>или а = b + 2 <br>или а - 2 = b | + | | a - b = 2 <br> или а = b + 2 <br> или а - 2 = b |
| | |- | | |- |
| - | | 3 | + | | 3 |
| - | | Девочек на 9 меньше, чем <br>мальчиков (как в 7В) | + | | Девочек на 9 меньше, чем мальчиков (как в 7В) |
| - | | b-а = 9 <br>или b = а + 9 <br>или а = b - 9 | + | | b - а = 9 <br> или b = а + 9 <br> или а = b - 9 |
| | |- | | |- |
| - | | 4 | + | | 4 |
| - | | Девочек в 2 раза больше, <br>чем мальчиков (как в 7Г) | + | | Девочек в 2 раза больше, чем мальчиков (как в 7Г) |
| - | | а = 2b | + | | а = 2b |
| | |- | | |- |
| - | | 5 | + | | 5 |
| - | | Девочек в 2 раза меньше, <br>чем мальчиков (как в 7В) | + | | Девочек в 2 раза меньше, чем мальчиков (как в 7В) |
| | | | | | |
| - | a=b:2 | + | a=b : 2 |
| | | | |
| - | или b= 2a | + | или b= 2a |
| | | | |
| | |- | | |- |
| - | | 6 | + | | 6 |
| - | | Если в данный класс придут <br>еще одна девочка и три маль- <br>чика, то девочек и мальчиков <br>станет поровну (как в 7А) | + | | Если в данный класс придут еще одна девочка и три мальчика, то девочек и мальчиков станет поровну (как в 7А) |
| - | | a+1=b+3 | + | | a+1=b+3 |
| | |- | | |- |
| - | | 7 | + | | 7 |
| - | | Если из класса уйдут три <br>девочки, то мальчиков станет <br>в 3 раза больше (как в 7В) | + | | Если из класса уйдут три девочки, то мальчиков станет в 3 раза больше (как в 7В) |
| - | | b=3(a-3) | + | | b=3(a - 3) |
| | |} | | |} |
| | | | |
| Строка 70: |
Строка 74: |
| | '''Пример 1.''' В классе девочек вдвое больше, чем мальчиков. Если из этого класса уйдут три девочки и придут три мальчика, то девочек будет на 4 больше, чем мальчиков. Сколько учеников в данном классе? | | '''Пример 1.''' В классе девочек вдвое больше, чем мальчиков. Если из этого класса уйдут три девочки и придут три мальчика, то девочек будет на 4 больше, чем мальчиков. Сколько учеников в данном классе? |
| | | | |
| - | '''Решение.''' Пусть х — число мальчиков в классе, тогда 2х — число девочек. Если уйдут три девочки, то останется Bх - 3) девочек. Если придут три мальчика, то станет (х + 3) мальчиков. По условию девочек будет тогда на 4 больше, чем мальчиков; на математическом языке это записывается так: | + | '''Решение.''' Пусть х — число мальчиков в классе, тогда 2х — число девочек. Если уйдут три девочки, то останется (х - 3) девочек. Если придут три мальчика, то станет (х + 3) мальчиков. По условию девочек будет тогда на 4 больше, чем мальчиков; на математическом языке это записывается так: |
| | | | |
| - | Bх - 3) - (х + 3) = 4. <br>Это уравнение — математическая модель задачи. Используя известные правила решения уравнений, последовательно получаем: <br>2x-3-x-3 = 4 (раскрыли скобки); <br>х - 6 = 4 (привели подобные слагаемые); <br>х = 6 + 4; <br>х - 10. <br>Теперь мы можем ответить на вопрос задачи. В классе 10 мальчиков, а значит, 20 девочек (вы помните, их по условию было в 2 раза больше).
| + | (х - 3) - (х + 3) = 4. <br> |
| | + | |
| | + | Это '''[[Решение уравнений|уравнение]]''' — математическая модель задачи. Используя известные правила решения уравнений, последовательно получаем: <br> |
| | + | |
| | + | 2x-3-x-3 = 4 (раскрыли скобки); <br>х - 6 = 4 (привели подобные слагаемые); <br>х = 6 + 4; <br>х - 10. <br> |
| | + | |
| | + | Теперь мы можем ответить на вопрос задачи. В классе 10 мальчиков, а значит, 20 девочек (вы помните, их по условию было в 2 раза больше). |
| | | | |
| | '''Ответ:''' всего в классе 30 учеников. <br>Обратим внимание на следующее обстоятельство: заметили ли вы, что в ходе решения было четкое разделение рассуждений на три этапа? | | '''Ответ:''' всего в классе 30 учеников. <br>Обратим внимание на следующее обстоятельство: заметили ли вы, что в ходе решения было четкое разделение рассуждений на три этапа? |
| | | | |
| - | На первом этапе, введя переменную х и переведя текст задачи на математический язык, мы составили математическую модель — в виде уравнения
| + | На первом этапе, введя переменную х и переведя текст задачи на математический язык, мы составили математическую модель — в виде уравнения |
| | | | |
| | (2х - 3) - (x + 3) = 4. | | (2х - 3) - (x + 3) = 4. |
| Строка 82: |
Строка 92: |
| | На втором этапе, используя наши знания, мы это уравнение решили, точнее, довели до самого простого вида (х = 10). На этом этапе мы не думали ни про девочек, ни про мальчиков, а занимались «чистой» математикой, работали только с математической моделью. | | На втором этапе, используя наши знания, мы это уравнение решили, точнее, довели до самого простого вида (х = 10). На этом этапе мы не думали ни про девочек, ни про мальчиков, а занимались «чистой» математикой, работали только с математической моделью. |
| | | | |
| - | На третьем этапе мы использовали полученное решение, чтобы ответить на вопрос задачи. На этом этапе мы снова вернулись к девочкам, мальчикам и интересующему нас классу. | + | На третьем этапе мы использовали полученное '''[[Графическое решение уравнений|решение]]''', чтобы ответить на вопрос задачи. На этом этапе мы снова вернулись к девочкам, мальчикам и интересующему нас классу. |
| | | | |
| | Подведем итоги. В процессе решения задачи были четко выделены три этапа: | | Подведем итоги. В процессе решения задачи были четко выделены три этапа: |
| Строка 92: |
Строка 102: |
| | Математические модели бывают не только алгебраические (в виде равенства с переменными, как в нашей таблице, или в виде уравнения, как было в примере 1). Для знакомства еще с одним видом математической модели возьмем задачу из учебника математики для 6 класса (специально берем задачу, с которой вы уже встречались). | | Математические модели бывают не только алгебраические (в виде равенства с переменными, как в нашей таблице, или в виде уравнения, как было в примере 1). Для знакомства еще с одним видом математической модели возьмем задачу из учебника математики для 6 класса (специально берем задачу, с которой вы уже встречались). |
| | | | |
| - | '''Пример 2.''' Построить график температуры воздуха, если известно, что температуру измеряли в течение суток и по результатам измерения составили следующую таблицу: | + | '''Пример 2.''' Построить '''[[Приклади графіків залежностей між величинами|график]]''' температуры воздуха, если известно, что температуру измеряли в течение суток и по результатам измерения составили следующую таблицу: |
| | | | |
| - | {| cellspacing="1" cellpadding="1" border="1" style="width: 878px; height: 45px;" | + | <br> |
| | + | |
| | + | {| cellspacing="1" cellpadding="1" border="1" style="width: 615px; height: 48px;" |
| | |- | | |- |
| - | | Время суток, ч | + | | Время суток, ч |
| - | | 0 | + | | 0 |
| - | | 2 | + | | 2 |
| - | | 4 | + | | 4 |
| - | | 6 | + | | 6 |
| - | | 8 | + | | 8 |
| - | | 10 | + | | 10 |
| - | | 11 | + | | 11 |
| - | | 14 | + | | 14 |
| - | | 16 | + | | 16 |
| - | | 18 | + | | 18 |
| - | | 22 | + | | 22 |
| - | | 24 | + | | 24 |
| | |- | | |- |
| - | | Температура, (X | + | | Температура, (X |
| - | | 5 | + | | 5 |
| - | | 0 | + | | 0 |
| - | | 0 | + | | 0 |
| - | | -3 | + | | -3 |
| - | | -4 | + | | -4 |
| - | | -2 | + | | -2 |
| - | | 0 | + | | 0 |
| - | | 6 | + | | 6 |
| - | | 8 | + | | 8 |
| - | | 5 | + | | 5 |
| - | | 3 | + | | 3 |
| - | | 3 | + | | 3 |
| | |} | | |} |
| | | | |
| - | '''<br>Решение.''' Построим прямоугольную систему координат. По горизонтальной оси (оси абсцисс) будем откладывать значения времени, а по вертикальной оси (оси ординат) — значения температуры. Построим на координатной плоскости точки, координатами которых являются соответствующие числа из таблицы. <br>Всего получается 12 точек (рис. 1). Соединив их плавной линией, получим один из возможных графиков температуры (рис. 2). | + | '''<br>Решение.''' Построим прямоугольную систему координат. По горизонтальной оси (оси абсцисс) будем откладывать значения времени, а по вертикальной оси (оси ординат) — значения температуры. Построим на координатной плоскости точки, координатами которых являются соответствующие числа из таблицы. |
| | | | |
| - | Построенный график есть математическая модель, описывающая зависимость температуры от времени. Анализируя этот график, можно описать словами, что происходило с температурой воздуха в течение суток. Ночью с 0 ч до 8 ч утра становилось все
| + | Всего получается 12 точек (рис. 1). Соединив их плавной линией, получим один из возможных графиков температуры (рис. 2). |
| | | | |
| | + | Построенный график есть математическая модель, описывающая зависимость температуры от времени. Анализируя этот график, можно описать словами, что происходило с температурой воздуха в течение суток. Ночью с 0 ч до 8 ч утра становилось все холоднее (от 5° в 0 ч до - 4° в 8 ч утра). |
| | | | |
| | + | <br> |
| | | | |
| - | [[Image:07-06-15.jpg]]<br><br>холоднее (от 5° в 0 ч до - 4° в 8 ч утра). Потом, видимо, выглянуло солнышко и стало теплеть, так что в 11 ч температура была уже не отрицательной, а нулевой ( 0°). До 16 ч теплело, причем в 16 ч было теплее всего (8°). А затем стало темнеть, температура начала постепенно снижаться и понизилась до 3° в 22 ч. Глядя на график температуры, можно определить, какая была наименьшая температура (- 4° в 8 ч утра), какая была наибольшая температура (8° в 16 ч), где температура менялась быстрее, где медленнее. | + | [[Image:07-06-15.jpg|480px|График температуры]]<br><br>Потом, видимо, выглянуло солнышко и стало теплеть, так что в 11 ч температура была уже не отрицательной, а нулевой ( 0°). До 16 ч теплело, причем в 16 ч было теплее всего (8°). А затем стало темнеть, температура начала постепенно снижаться и понизилась до 3° в 22 ч. Глядя на график температуры, можно определить, какая была наименьшая температура (- 4° в 8 ч утра), какая была наибольшая температура (8° в 16 ч), где температура менялась быстрее, где медленнее. |
| | | | |
| - | Рассмотренную математическую модель называют графической моделью. Итак, нам нужно учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая модель), графически (графическая модель). Бывают еще геометрические модели реальных ситуаций — они изучаются в курсе геометрии. Впрочем, графические модели также иногда называют геометрическими, а вместо термина «алгебраическая модель» <br>употребляют термин «аналитическая модель». <br>Все это — виды математических моделей. <br><br> | + | Рассмотренную математическую модель называют графической моделью. Итак, нам нужно учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая модель), графически (графическая модель). Бывают еще геометрические модели реальных ситуаций — они изучаются в курсе геометрии. Впрочем, графические модели также иногда называют геометрическими, а вместо термина «алгебраическая модель» употребляют термин «аналитическая модель». |
| | + | |
| | + | Все это — виды математических моделей. <br><br> |
| | | | |
| | <br> | | <br> |
| | | | |
| | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 7 класса [[Математика|скачать]]</sub> <br> | | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 7 класса [[Математика|скачать]]</sub> <br> |
| | + | |
| | + | <br> |
| | + | |
| | + | ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 18:52, 14 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Что такое математическая модель
Что такое математическая модель
Представьте себе такую ситуацию: в школе четыре седьмых класса.
В 7А учатся 15 девочек и 13 мальчиков,
в 7Б — 12 девочек и 12 мальчиков,
в 7В — 9 девочек и 18 мальчиков,
в 7Г — 20 девочек и 10 мальчиков.
Если нам нужно ответить на вопрос, сколько учеников в каждом из седьмых классов, то нам 4 раза придется осуществлять одну и ту же операцию сложения:
в 7А 15 + 13 = 28 учеников;
в 7Б 12 +12 = 24 ученика;
в 7В 9 + 18 = 27 учеников;
в 7Г 20 + 10 = 30 учеников.
Используя математический язык, можно все эти четыре разные ситуации объединить: в классе учатся а девочек и b мальчиков, значит, всего учеников а + b. Эту запись а + b называют математической моделью данной реальной ситуации. Алгебра в основном занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.
В следующей таблице приведены различные реальные ситуации и их математические модели; при этом а — число девочек в классе, 6 — число мальчиков в том же классе.
| №
| Реальная ситуация
| Математическая модель
|
| 1
| В классе девочек и мальчиков поровну (как в 7Б)
| a = b
|
| 2
| Девочек на 2 больше, чем мальчиков (как в 7А)
| a - b = 2
или а = b + 2
или а - 2 = b
|
| 3
| Девочек на 9 меньше, чем мальчиков (как в 7В)
| b - а = 9
или b = а + 9
или а = b - 9
|
| 4
| Девочек в 2 раза больше, чем мальчиков (как в 7Г)
| а = 2b
|
| 5
| Девочек в 2 раза меньше, чем мальчиков (как в 7В)
|
a=b : 2
или b= 2a
|
| 6
| Если в данный класс придут еще одна девочка и три мальчика, то девочек и мальчиков станет поровну (как в 7А)
| a+1=b+3
|
| 7
| Если из класса уйдут три девочки, то мальчиков станет в 3 раза больше (как в 7В)
| b=3(a - 3)
|
Составляя эту таблицу, мы шли от реальной ситуации к ее математической модели. Не надо уметь двигаться и в обратном направлении, т.е. по заданной математической модели описывать словами реальную ситуацию. Например, что означает (при тех же обозначениях, что и в нашей таблице) такая математическая модель: а - 5 = 6 + 5? Она означает, что если из класса уйдут 5 девочек и придут 5 мальчиков, то девочек и мальчиков в классе станет поровну (эта ситуация имеет место в 7Г из рассмотренного примера).
Наверное, у вас возник вопрос: а зачем нужна математическая модель реальной ситуации, что она нам дает, кроме краткой выразительной записи? Чтобы ответить на этот вопрос, решим следующую задачу.
Пример 1. В классе девочек вдвое больше, чем мальчиков. Если из этого класса уйдут три девочки и придут три мальчика, то девочек будет на 4 больше, чем мальчиков. Сколько учеников в данном классе?
Решение. Пусть х — число мальчиков в классе, тогда 2х — число девочек. Если уйдут три девочки, то останется (х - 3) девочек. Если придут три мальчика, то станет (х + 3) мальчиков. По условию девочек будет тогда на 4 больше, чем мальчиков; на математическом языке это записывается так:
(х - 3) - (х + 3) = 4.
Это уравнение — математическая модель задачи. Используя известные правила решения уравнений, последовательно получаем:
2x-3-x-3 = 4 (раскрыли скобки);
х - 6 = 4 (привели подобные слагаемые);
х = 6 + 4;
х - 10.
Теперь мы можем ответить на вопрос задачи. В классе 10 мальчиков, а значит, 20 девочек (вы помните, их по условию было в 2 раза больше).
Ответ: всего в классе 30 учеников.
Обратим внимание на следующее обстоятельство: заметили ли вы, что в ходе решения было четкое разделение рассуждений на три этапа?
На первом этапе, введя переменную х и переведя текст задачи на математический язык, мы составили математическую модель — в виде уравнения
(2х - 3) - (x + 3) = 4.
На втором этапе, используя наши знания, мы это уравнение решили, точнее, довели до самого простого вида (х = 10). На этом этапе мы не думали ни про девочек, ни про мальчиков, а занимались «чистой» математикой, работали только с математической моделью.
На третьем этапе мы использовали полученное решение, чтобы ответить на вопрос задачи. На этом этапе мы снова вернулись к девочкам, мальчикам и интересующему нас классу.
Подведем итоги. В процессе решения задачи были четко выделены три этапа:
Первый этап. Составление математической модели.
Второй этап. Работа с математической моделью.
Третий этап. Ответ на вопрос задачи.
Вот так обычно применяется математика к реальной действительности. После рассмотренного примера повторим вопрос: как вы думаете, нужны ли математические модели и надо ли уметь работать с ними? Нужны! Разумеется, чем сложнее модель, тем больше фактов, правил, свойств приходится применять для ее упрощения. Эти факты, правила, свойства надо изучить, что мы и будем с вами делать.
Математические модели бывают не только алгебраические (в виде равенства с переменными, как в нашей таблице, или в виде уравнения, как было в примере 1). Для знакомства еще с одним видом математической модели возьмем задачу из учебника математики для 6 класса (специально берем задачу, с которой вы уже встречались).
Пример 2. Построить график температуры воздуха, если известно, что температуру измеряли в течение суток и по результатам измерения составили следующую таблицу:
| Время суток, ч
| 0
| 2
| 4
| 6
| 8
| 10
| 11
| 14
| 16
| 18
| 22
| 24
|
| Температура, (X
| 5
| 0
| 0
| -3
| -4
| -2
| 0
| 6
| 8
| 5
| 3
| 3
|
Решение. Построим прямоугольную систему координат. По горизонтальной оси (оси абсцисс) будем откладывать значения времени, а по вертикальной оси (оси ординат) — значения температуры. Построим на координатной плоскости точки, координатами которых являются соответствующие числа из таблицы.
Всего получается 12 точек (рис. 1). Соединив их плавной линией, получим один из возможных графиков температуры (рис. 2).
Построенный график есть математическая модель, описывающая зависимость температуры от времени. Анализируя этот график, можно описать словами, что происходило с температурой воздуха в течение суток. Ночью с 0 ч до 8 ч утра становилось все холоднее (от 5° в 0 ч до - 4° в 8 ч утра).
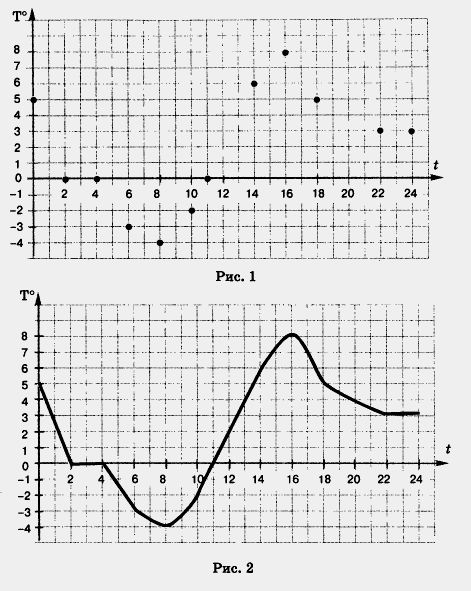
Потом, видимо, выглянуло солнышко и стало теплеть, так что в 11 ч температура была уже не отрицательной, а нулевой ( 0°). До 16 ч теплело, причем в 16 ч было теплее всего (8°). А затем стало темнеть, температура начала постепенно снижаться и понизилась до 3° в 22 ч. Глядя на график температуры, можно определить, какая была наименьшая температура (- 4° в 8 ч утра), какая была наибольшая температура (8° в 16 ч), где температура менялась быстрее, где медленнее.
Рассмотренную математическую модель называют графической моделью. Итак, нам нужно учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая модель), графически (графическая модель). Бывают еще геометрические модели реальных ситуаций — они изучаются в курсе геометрии. Впрочем, графические модели также иногда называют геометрическими, а вместо термина «алгебраическая модель» употребляют термин «аналитическая модель».
Все это — виды математических моделей.
Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 7 класса скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











