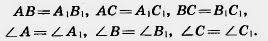|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Треугольник</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Треугольник, вершины треугольника, угол, отрезки</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Треугольник''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Треугольник''' |
| | | | |
| | + | <br> ''' '''[[Треугольник. Полные уроки|'''Треугольник''']] |
| | | | |
| - | ''' ТРЕУГОЛЬНИК''' | + | <br>'''''Треугольником''''' называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются '''[[Презентація уроку на тему «Трикутник і його елементи»|вершинами треугольника]]''', а отрезки — '''''сторонами'''''. |
| | | | |
| - | <br>'''''Треугольником''''' называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются '''''вершинами''''' треугольника, а отрезки — '''''сторонами'''''.
| + | На рисунке 21 вы видите треугольник с вершинами А, В, С и сторонами АВ, ВС, АС. Треугольник обозначается указанием его вершин. Вместо слова «треугольник» иногда употребляют знак [[Image:20-06-54.jpg|Треугольник]]. Например, треугольник на рисунке 21 обозначается так: [[Image:20-06-54.jpg|Треугольник]] ABC. |
| | | | |
| - | На рисунке 21 вы видите треугольник с вершинами А, В, С и сторонами АВ, ВС, АС. Треугольник обозначается указанием его вершин. Вместо слова «треугольник» иногда употребляют знак [[Image:20-06-54.jpg]]. Например, треугольник на рисунке 21 обозначается так: [[Image:20-06-54.jpg]] ABC.<br>Углом треугольника ABC при вершине А называется угол, образованный полупрямыми АВ и АС. Так же определяются углы треугольника при вершинах В и С.<br>Два отрезка называются равными, если они имеют одинаковую длину. Два угла называются равными, если они имеют одинаковую угловую меру в градусах.<br>Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.<br>
| + | Углом треугольника ABC при вершине А называется '''[[Практикум на тему «Суміжні кути, їх властивості»|Угол]]''', образованный полупрямыми АВ и АС. Так же определяются углы треугольника при вершинах В и С. |
| | | | |
| - | [[Image:20-06-55.jpg]]<br> <br>На рисунке 22 вы видите два равных треугольника ABC и A1B1C1. У них<br>АВ = А,В,, АС = А,С,, BC = BiCi, ^A=AAi, AB=ABi, ^C=^Ct. На чертеже равные отрезки обычно отмечают одной, двумя или тремя черточками, а равные углы — одной, двумя или тремя дужками.<br>Для обозначения равенства треугольников используется обычный знак равенства: =. Запись ААВС= AAIB\C\ читается так: «Треугольник ABC равен треугольнику A]BiCi*. При этом имеет значение порядок, в котором записываются вершины треугольника. Равенство ААВС— AAiB\C\ означает, что /_А= AAi, АВ= ABi, ... . А равенство ААВС= AB,A,C^ означает уже совсем другое: АА— /LBx, /-В= /^А\, ... .<br>Задача (38). Треугольники ABC и PQR равны. Известно, что сторона АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R1 Объясните ответ.<br>Решение. Так как треугольники ABC и PQR равны, тоунихЛВ = Ре, ZC= zifi. Значит, PQ= Юм, ^Д = 90°.<br> | + | Два отрезка называются равными, если они имеют одинаковую длину. Два угла называются равными, если они имеют одинаковую угловую меру в градусах. |
| | + | |
| | + | Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.<br> |
| | + | |
| | + | [[Image:20-06-55.jpg|480px|Треугольники]]<br> <br>На рисунке 22 вы видите два равных треугольника ABC и A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>. <br> |
| | + | |
| | + | [[Image:20-06-56.jpg|480px|Обозначения равности треугольников]] |
| | + | |
| | + | На чертеже равные '''[[Измерение отрезков. Полные уроки|отрезки]]''' обычно отмечают одной, двумя или тремя черточками, а равные углы — одной, двумя или тремя дужками. |
| | + | |
| | + | Для обозначения равенства треугольников используется обычный знак равенства: =. Запись [[Image:20-06-54.jpg|Треугольник]]АВС= [[Image:20-06-54.jpg|Треугольник]]A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> читается так: «Треугольник ABC равен треугольнику A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>. При этом имеет значение порядок, в котором записываются вершины треугольника. Равенство [[Image:20-06-54.jpg|Треугольник]]АВС— [[Image:20-06-54.jpg|Треугольник]]A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> означает, что |
| | + | |
| | + | [[Image:20-06-47.jpg|Угол]]А= [[Image:20-06-47.jpg|Угол]]A<sub>1</sub>, [[Image:20-06-47.jpg|Угол]]В= [[Image:20-06-47.jpg|Угол]]B<sub>1</sub>, ... . А равенство [[Image:20-06-54.jpg|Треугольник]]АВС= [[Image:20-06-54.jpg|Треугольник]]A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> означает уже совсем другое: [[Image:20-06-47.jpg|Угол]]А= [[Image:20-06-47.jpg|Угол]]B<sub>1</sub>, [[Image:20-06-47.jpg|Угол]]В=[[Image:20-06-47.jpg|Угол]]А<sub>1</sub>, ... .<br>Задача (38). Треугольники ABC и PQR равны. Известно, что сторона АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R1 Объясните ответ. |
| | + | |
| | + | Решение. Так как треугольники ABC и PQR равны, то у них AВ = PQ, [[Image:20-06-47.jpg|Угол]]C= [[Image:20-06-47.jpg|Угол]]R. Значит, PQ= 10м, [[Image:20-06-47.jpg|Угол]]R = 90°.<br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Планирование математике, материалы по математике 7 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | + | <br> <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:48, 15 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Треугольник
Треугольник
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — сторонами.
На рисунке 21 вы видите треугольник с вершинами А, В, С и сторонами АВ, ВС, АС. Треугольник обозначается указанием его вершин. Вместо слова «треугольник» иногда употребляют знак  . Например, треугольник на рисунке 21 обозначается так: . Например, треугольник на рисунке 21 обозначается так:  ABC. ABC.
Углом треугольника ABC при вершине А называется Угол, образованный полупрямыми АВ и АС. Так же определяются углы треугольника при вершинах В и С.
Два отрезка называются равными, если они имеют одинаковую длину. Два угла называются равными, если они имеют одинаковую угловую меру в градусах.
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
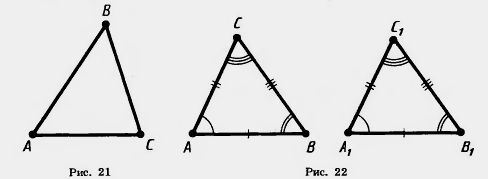
На рисунке 22 вы видите два равных треугольника ABC и A1B1C1.
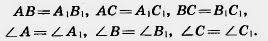
На чертеже равные отрезки обычно отмечают одной, двумя или тремя черточками, а равные углы — одной, двумя или тремя дужками.
Для обозначения равенства треугольников используется обычный знак равенства: =. Запись  АВС= АВС=  A1B1C1 читается так: «Треугольник ABC равен треугольнику A1B1C1. При этом имеет значение порядок, в котором записываются вершины треугольника. Равенство A1B1C1 читается так: «Треугольник ABC равен треугольнику A1B1C1. При этом имеет значение порядок, в котором записываются вершины треугольника. Равенство  АВС— АВС—  A1B1C1 означает, что A1B1C1 означает, что
 А= А=  A1, A1,  В= В=  B1, ... . А равенство B1, ... . А равенство  АВС= АВС=  A1B1C1 означает уже совсем другое: A1B1C1 означает уже совсем другое:  А= А=  B1, B1,  В= В= А1, ... . А1, ... .
Задача (38). Треугольники ABC и PQR равны. Известно, что сторона АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R1 Объясните ответ.
Решение. Так как треугольники ABC и PQR равны, то у них AВ = PQ,  C= C=  R. Значит, PQ= 10м, R. Значит, PQ= 10м,  R = 90°. R = 90°.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|