|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Существование, единственность перпендикуляра к прямой</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Существование, единственность перпендикуляра к прямой, перпендикуляр, теорема, параллельные прямые, секущая</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Существование и единственность перпендикуляра к прямой''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика:Существование и единственность перпендикуляра к прямой''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ПЕРПЕНДИКУЛЯРА К ПРЯМОЙ'''<br> | + | ''' Существование и единственность ''' |
| | | | |
| - | <br>Теорема 4.6. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один. | + | ''' перпендикуляра к прямой'''<br> |
| | | | |
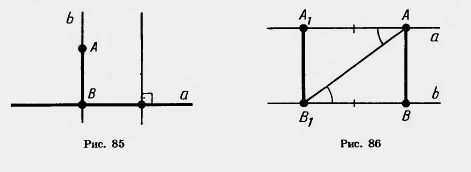
| - | Доказательство. Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к прямой а.<br>
| + | <br>Теорема 4.6. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую '''[[Шпаргалки на тему «Паралельні та перпендикулярні прямі, їх властивості. Доведення від супротивного»|перпендикуляр]]''', и только один. |
| | | | |
| - | Докажем единственность перпендикуляра АВ. Допустим,<br> <br>[[Image:21-06-32.jpg]]<br><br> <br>существует другой перпендикуляр АС. Тогда у треугольника ABC будут два прямых угла. А это, как мы знаем, невозможно. Теорема доказана.
| + | Доказательство. Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к прямой а.<br> |
| | | | |
| - | Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.<br>
| + | Докажем единственность перпендикуляра АВ. Допустим,<br> <br>[[Image:21-06-32.jpg|480px|Единственность перпендикуляра]]<br><br> <br>существует другой перпендикуляр АС. Тогда у треугольника ABC будут два прямых угла. А это, как мы знаем, невозможно. '''[[Обратная теорема. Полные уроки|Теорема]]''' доказана. |
| | | | |
| - | Задача (50). Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.<br>
| + | Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.<br> |
| | | | |
| - | Решение. Пусть а и b — параллельные прямые и А, А<sub>1</sub><sub></sub> — любые точки на прямой а (рис. 86). Опустим из точки А<sub>1</sub> перпендикуляр А<sub>1</sub>В<sub>1</sub> на прямую b. <br>
| + | Задача (50). Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.<br> |
| | | | |
| - | Отложим из точки B<sub>1</sub> на прямой b отрезок В<sub>1</sub>В, равный отрезку АА<sub>1</sub>, так, чтобы точки A<sub>1</sub> и В были по разные стороны прямой АВ<sub>1</sub>.
| + | Решение. Пусть а и b — '''[[Параллельные прямые. Полные уроки|параллельные прямые]]''' и А, А<sub>1</sub><sub></sub> — любые точки на прямой а (рис. 86). Опустим из точки А<sub>1</sub> перпендикуляр А<sub>1</sub>В<sub>1</sub> на прямую b. <br> |
| | | | |
| - | Тогда треугольники АВ<sub>1</sub>А, и B<sub>1</sub>AB равны по первому признаку. У них сторона AB<sub>1</sub> общая, А А <sub>1</sub> =ВВ<sub>1</sub> по построению, а углы В<sub>1</sub>АА<sub>1</sub> и АВ<sub>1</sub>В равны как внутренние накрест лежащие параллельных а и b с секущей AB<sub>1</sub>.
| + | Отложим из точки B<sub>1</sub> на прямой b отрезок В<sub>1</sub>В, равный отрезку АА<sub>1</sub>, так, чтобы точки A<sub>1</sub> и В были по разные стороны прямой АВ<sub>1</sub>. |
| | | | |
| - | Из равенства треугольников следует, что АВ есть перпендикуляр к прямой b и AB=A<sub>1</sub>B<sub>1</sub> что и требовалось доказать.
| + | Тогда треугольники АВ<sub>1</sub>А, и B<sub>1</sub>AB равны по первому признаку. У них сторона AB<sub>1</sub> общая, А А <sub>1</sub> =ВВ<sub>1</sub> по построению, а углы В<sub>1</sub>АА<sub>1</sub> и АВ<sub>1</sub>В равны как внутренние накрест лежащие параллельных а и b с '''[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|секущей]]''' AB<sub>1</sub>. |
| | | | |
| - | Как видим, расстояния от всех точек прямой до параллельной прямой равны. Поэтому говорят, что параллельные прямые равноотстоящие.<br>Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой. | + | Из равенства треугольников следует, что АВ есть перпендикуляр к прямой b и AB=A<sub>1</sub>B<sub>1</sub> что и требовалось доказать. |
| | + | |
| | + | Как видим, расстояния от всех точек прямой до параллельной прямой равны. Поэтому говорят, что параллельные прямые равноотстоящие. |
| | + | |
| | + | Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой. |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 7 класса [[Математика|скачать]], календарно-тематическое планирование</sub> | + | <br> [http://xvatit.com/relax/fun-videos/ '''<sub>Видео</sub>''']<sub>по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Доказательство. Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к прямой а.
Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.
Задача (50). Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.
Как видим, расстояния от всех точек прямой до параллельной прямой равны. Поэтому говорят, что параллельные прямые равноотстоящие.
Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.