KNOWLEDGE HYPERMARKET

Задачи-4(7 класс)
(Создана новая страница размером <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, ...)
 
(1 промежуточная версия не показана)
Строка 1: Строка 1:
-
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Задачи-4(7 класс)</metakeywords>  
+
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Задачи, параллельные прямые, отрезки, треугольники, секущая, угол, равнобедренный треугольник, биссектриса, медиана</metakeywords>  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 7 класс|Математика 7 класс]]&gt;&gt;Математика:Задачи-4(7 класс)'''  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 7 класс|Математика 7 класс]]&gt;&gt;Математика:Задачи-4(7 класс)'''  
Строка 5: Строка 5:
<br>  
<br>  
-
'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ЗАДАЧИ'''
+
'''&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Задачи'''  
-
<br>1. Докажите, что если некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.<br>Докажите, что если две прямые пересекаются, то любая третья прямая пересекает по крайней мере одну из этих прямых. <br>3.&nbsp;&nbsp; &nbsp;Дано: a||b||c||d. Докажите, что a||d.
+
<br>1. Докажите, что если некоторая прямая пересекает одну из двух '''[[Параллельные прямые. Полные уроки|параллельных прямых]]''', то она пересекает и другую.<br>Докажите, что если две прямые пересекаются, то любая третья прямая пересекает по крайней мере одну из этих прямых.  
-
4.&nbsp;&nbsp; &nbsp;Прямые АВ и CD параллельны. Докажите, что если отрезок ВС пересекает прямзгю AD, то точка пересечения принадлежит отрезку AD (см. рис. 70).
+
3. Дано: a||b||c||d. Докажите, что a||d.  
-
5. Дан треугольник ABC. На стороне АВ отмечена точка B<sub>1</sub>, а на стороне АС — точка С<sub>1</sub>(рис. 87). Назовите внутренние односторонние и внутренние накрест лежащие углы при прямых АВ, АС и секущей В<sub>1</sub>С<sub>1</sub>
+
4. Прямые АВ и CD параллельны. Докажите, что если отрезок ВС пересекает прямую AD, то точка пересечения принадлежит отрезку AD (см. рис. 70).  
-
6.&nbsp;&nbsp; &nbsp;Назовите внутренние накрест лежащие и внутренние односторонние углы на рисунке 72.
+
5. Дан треугольник ABC. На стороне АВ отмечена точка B<sub>1</sub>, а на стороне АС — точка С<sub>1</sub>(рис. 87). Назовите внутренние односторонние и внутренние накрест лежащие углы при прямых АВ, АС и секущей В<sub>1</sub>С<sub>1</sub>
-
7.&nbsp;&nbsp; &nbsp;Отрезки AD и ВС пересекаются. Для прямых АС и BD и секущей ВС назовите пару внутренних накрест лежащих углов. Для тех же прямых и секущей АВ назовите пару внутренних односторонних углов. Объясните ответ.
+
6. Назовите внутренние накрест лежащие и внутренние односторонние углы на рисунке 72.  
-
8. Даны прямая АВ и точка С, не лежащая на этой прямой. Докажите, что через точку С можно провести прямзгю, параллельную прямой АВ. 9. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных параллельными и секущей, параллельны, т. е. лежат на параллельных прямых.
+
7. '''[[Измерение отрезков. Полные уроки|Отрезки]]''' AD и ВС пересекаются. Для прямых АС и BD и секущей ВС назовите пару внутренних накрест лежащих углов. Для тех же прямых и секущей АВ назовите пару внутренних односторонних углов. Объясните ответ.  
-
10.&nbsp;&nbsp; &nbsp;Отрезки АВ и CD пересекаются в точке Е и делятся этой точкой пополам. Докажите, что прямые АС и BD параллельны.
+
8. Даны прямая АВ и точка С, не лежащая на этой прямой. Докажите, что через точку С можно провести прямзгю, параллельную прямой АВ. 9. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных параллельными и секущей, параллельны, т. е. лежат на параллельных прямых.  
-
11.&nbsp;&nbsp; &nbsp;Треугольники ABC и BAD равны. Точки С и D лежат по разные стороны от прямой АВ. Докажите, что прямые АС и BD параллельны.
+
10. Отрезки АВ и CD пересекаются в точке Е и делятся этой точкой пополам. Докажите, что прямые АС и BD параллельны.  
-
12. Угол ABC равен 80°, а угол BCD равен 120°. Могут ли прямые АВ и CD быть параллельными? Обоснуйте ответ.
+
11. '''[[Презентація уроку на тему «Трикутник і його елементи»|Треугольники]]''' ABC и BAD равны. Точки С и D лежат по разные стороны от прямой АВ. Докажите, что прямые АС и BD параллельны.  
-
13.&nbsp;&nbsp; &nbsp;Прямые АС и BD параллельны, причем точки А и D лежат по разные стороны от секущей ВС (рис. 77). Докажите, что:
+
12. Угол ABC равен 80°, а угол BCD равен 120°. Могут ли прямые АВ и CD быть параллельными? Обоснуйте ответ.  
-
1) углы DBC и АСВ внутренние накрест лежащие относительно секущей ВС;
+
13. Прямые АС и BD параллельны, причем точки А и D лежат по разные стороны от секущей ВС (рис. 77). Докажите, что:
 +
 
 +
1) углы DBC и АСВ внутренние накрест лежащие относительно '''[[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|секущей]]''' ВС;  
2) луч ВС проходит между сторонами угла ABD;  
2) луч ВС проходит между сторонами угла ABD;  
-
3) углы CAB и DBA внутренние односторонние относительно секущей АВ.
+
3) углы CAB и DBA внутренние односторонние относительно секущей АВ.  
-
14.&nbsp;&nbsp; &nbsp;1) Разность двух внутренних односторонних углов при двух параллельных прямых и секущей равна 30°, Найдите эти углы.<br>2) Сумма двух внутренних накрест лежащих углов при двух параллельных прямых и секущей равна 150°. Чему равны эти углы?
+
14. 1) Разность двух внутренних односторонних углов при двух параллельных прямых и секущей равна 30°, Найдите эти углы.<br>2) Сумма двух внутренних накрест лежащих углов при двух параллельных прямых и секущей равна 150°. Чему равны эти углы?  
-
15.&nbsp;&nbsp; &nbsp;Один из углов, которые получаются при пересечении двух параллельных прямых секущей, равен 72°. Найдите остальные семь углов.
+
15. Один из углов, которые получаются при пересечении двух параллельных прямых секущей, равен 72°. Найдите остальные семь углов.  
-
16.&nbsp;&nbsp; &nbsp;Один из углов, которые получаются при пересечении двух параллельных прямых секущей, равен 30°. Может ли один из остальных семи углов равняться 70°? Объясните ответ.
+
16. Один из углов, которые получаются при пересечении двух параллельных прямых секущей, равен 30°. Может ли один из остальных семи углов равняться 70°? Объясните ответ.  
17. Докажите, что две прямые, параллельные перпендикулярным прямым, сами перпендикулярны.  
17. Докажите, что две прямые, параллельные перпендикулярным прямым, сами перпендикулярны.  
-
18. Найдите неизвестный угол треугольника, если у него два угла равны:  
+
18. Найдите неизвестный '''[[Практикум на тему «Суміжні кути, їх властивості»|угол]]''' треугольника, если у него два угла равны:  
-
1) 50° и 30°; 2) 40° и 75°; 3) 65°и 80°; 4) 25° и 120°.
+
1) 50° и 30°; 2) 40° и 75°; 3) 65°и 80°; 4) 25° и 120°.  
-
19.&nbsp;&nbsp; &nbsp;Найдите углы треугольника, если они пропорциональны числам:  
+
19. Найдите углы треугольника, если они пропорциональны числам:  
1) 1, 2, 3;  
1) 1, 2, 3;  
-
2) 2, 3, 4;
+
2) 2, 3, 4;  
-
3) 3, 4, 5;
+
3) 3, 4, 5;  
-
4) 4, 5, 6;
+
4) 4, 5, 6;  
-
5) 5, 6, 7.
+
5) 5, 6, 7.  
-
20.&nbsp;&nbsp; &nbsp;Может ли в треугольнике быть:
+
20. Может ли в треугольнике быть:  
-
1) два тупых угла;
+
1) два тупых угла;  
-
2) тупой и прямой углы;
+
2) тупой и прямой углы;  
-
3) два прямых угла?
+
3) два прямых угла?  
-
21.&nbsp;&nbsp; &nbsp;Может ли быть тупым угол при основании равнобедренного треугольника?
+
21. Может ли быть тупым угол при основании равнобедренного треугольника?  
-
22.&nbsp;&nbsp; &nbsp;Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании у него равен:<br>1)&nbsp;&nbsp; &nbsp;40°; 2) 55°; 3) 72°.
+
22. Найдите угол между боковыми сторонами '''[[Свойство медианы равнобедренного треугольника. Полные уроки|равнобедренного треугольника]]''', если угол при основании у него равен:<br>1)&nbsp;&nbsp; &nbsp;40°; 2) 55°; 3) 72°.  
-
23.&nbsp;&nbsp; &nbsp;Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами равен:
+
23. Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами равен:  
-
1) 80°; 2) 120°; 3) 30°.
+
1) 80°; 2) 120°; 3) 30°.  
-
24.&nbsp;&nbsp; &nbsp;Один из углов равнобедренного треугольника равен 100°. Найдите остальные углы.
+
24. Один из углов равнобедренного треугольника равен 100°. Найдите остальные углы.  
-
25.&nbsp;&nbsp; &nbsp;Один из углов равнобедренного треугольника равен 70°. Найдите остальные углы. Сколько решений имеет задача?
+
25. Один из углов равнобедренного треугольника равен 70°. Найдите остальные углы. Сколько решений имеет задача?  
-
26.&nbsp;&nbsp; &nbsp;Докажите, что если один из углов равнобедренного треугольника равен 60°, то этот треугольник равносторонний.
+
26. Докажите, что если один из углов равнобедренного треугольника равен 60°, то этот треугольник равносторонний.  
-
27.&nbsp;&nbsp; &nbsp;В равнобедренном треугольнике ABC с основанием АС проведена биссектриса CD. Найдите углы треугольника ABC, если угол ADC равен:
+
27. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса CD. Найдите углы треугольника ABC, если угол ADC равен:  
-
1) 60°; 2) 75°; 3) а.
+
1) 60°; 2) 75°; 3) а.  
-
28.&nbsp;&nbsp; &nbsp;В равнобедренном треугольнике AВС с основанием АС и углом при вершине В, равным 36°, проведена биссектриса AD. Докажите, что треугольники CDA и ADB равнобедренные (рис. 88).<br><br>[[Image:21-06-34.jpg]]
+
28. В равнобедренном треугольнике AВС с основанием АС и углом при вершине В, равным 36°, проведена биссектриса AD. Докажите, что треугольники CDA и ADB равнобедренные (рис. 88).<br><br>[[Image:21-06-34.jpg|480px|Треугольники]]  
 +
<br>
 +
[[Image:21-06-36.jpg|480px|Треугольник]]&nbsp;<br>
-
[[Image:21-06-35.jpg]]&nbsp;<br>
+
29. В треугольнике ABC проведены '''[[Кути. Вимірювання кутів. Бісектриса кута|биссектрисы]]''' из вершин А и В. Точка их пересечения обозначена D. Найдите угол ADB, если:
-
<br>29.&nbsp;&nbsp; &nbsp;В треугольнике ABC проведены биссектрисы из вершин А и В. Точка их пересечения обозначена D. Найдите угол ADB, если:
+
1) [[Image:20-06-61.jpg|Угол]]A = 50[[Image:20-06-61.jpg|Угол]]B= 100°;  
-
1) [[Image:20-06-61.jpg]]A = 50[[Image:20-06-61.jpg]]B= 100°;
+
2)[[Image:20-06-61.jpg|Угол]]A = a, [[Image:20-06-61.jpg|Угол]]B=b;  
-
2)[[Image:20-06-61.jpg]]A = a, [[Image:20-06-61.jpg]]B=b;
+
3) [[Image:20-06-61.jpg|Угол]]C = 130°;  
-
3) [[Image:20-06-61.jpg]]C = 130°;
+
4) [[Image:20-06-61.jpg|Угол]]C = y.
-
4) [[Image:20-06-61.jpg]]C = y.
+
30. Чему равны углы равностороннего треугольника?
-
30.&nbsp;&nbsp; &nbsp;Чему равны углы равностороннего треугольника?
+
31. Под каким углом пересекаются биссектрисы двух внутренних односторонних углов при параллельных прямых?  
-
31.&nbsp;&nbsp; &nbsp;Под каким углом пересекаются биссектрисы двух внутренних односторонних углов при параллельных прямых?
+
32. Один из внешних углов равнобедренного треугольника равен 70°. Найдите углы треугольника.
-
32. Один из внешних углов равнобедренного треугольника равен 70°. Найдите углы треугольника.
+
33. Найдите углы треугольника, зная, что внешние углы при двух его вершинах равны 120° и 150°.  
-
33.&nbsp;&nbsp; &nbsp;Найдите углы треугольника, зная, что внешние углы при двух его вершинах равны 120° и 150°.
+
34. Два внешних угла треугольника равны 100° и 150°. Найдите третий внешний угол.  
-
34.&nbsp;&nbsp; &nbsp;Два внешних угла треугольника равны 100° и 150°. Найдите третий внешний угол.
+
35. В треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими, если углы А тл В треугольника острые?
-
35.&nbsp;&nbsp; &nbsp;В треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими, если углы А тл В треугольника острые?
+
36. В треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими, если угол А тупой? Обоснуйте ответ.
-
36.&nbsp;&nbsp; &nbsp;В треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими, если угол А тупой? Обоснуйте ответ.
+
37. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.  
-
37.&nbsp;&nbsp; &nbsp;Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.
+
38. Сумма внешних углов треугольника ABC при вершинах А и В, взятых по одному для каждой вершины, равна 240°. Чему равен угол С треугольника?
-
38.&nbsp;&nbsp; &nbsp;Сумма внешних углов треугольника ABC при вершинах А и В, взятых по одному для каждой вершины, равна 240°. Чему равен угол С треугольника?
+
39. Дан треугольник ABC. На продолжении стороны АС отложены отрезки AD=AB и СЕ = СВ (рис. 89). Как найти углы треугольника DBE, зная углы треугольника АВС?  
-
39.&nbsp;&nbsp; &nbsp;Дан треугольник ABC. На продолжении стороны АС отложены отрезки AD=AB и СЕ = СВ (рис. 89). Как найти углы треугольника DBE, зная углы треугольника АВС?
+
40. У треугольника один из внутренних углов равен 30°, а один из внешних 40°. Найдите остальные внутренние углы треугольника.  
-
 
+
-
40.&nbsp;&nbsp; &nbsp;У треугольника один из внутренних углов равен 30°, а один из внешних 40°. Найдите остальные внутренние углы треугольника.
+
41. Из вершины прямого угла треугольника ABC проведена высота BD. Найдите угол CBD, зная, что:  
41. Из вершины прямого угла треугольника ABC проведена высота BD. Найдите угол CBD, зная, что:  
-
1) [[Image:20-06-61.jpg]]A=20°; 2)[[Image:20-06-61.jpg]].A = 65°; 3) [[Image:20-06-61.jpg]]A=а.
+
1) [[Image:20-06-61.jpg|Угол]]A=20°; 2)[[Image:20-06-61.jpg|Угол]].A = 65°; 3) [[Image:20-06-61.jpg|Угол]]A=а.  
-
42.&nbsp;&nbsp; &nbsp;Из вершины тупого угла В треугольника ABC проведена высота BD. Найдите углы треугольников ABD и CBD, зная, что [[Image:20-06-61.jpg]]A = a, [[Image:20-06-61.jpg]]B= в.
+
42. Из вершины тупого угла В треугольника ABC проведена высота BD. Найдите углы треугольников ABD и CBD, зная, что [[Image:20-06-61.jpg|Угол]]A = a, [[Image:20-06-61.jpg|Угол]]B= в.  
-
43.&nbsp;&nbsp; &nbsp;Докажите, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.
+
43. Докажите, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.  
-
44.&nbsp;&nbsp; &nbsp;Найдите углы прямоугольного равнобедренного треугольника.
+
44. Найдите углы прямоугольного равнобедренного треугольника.  
-
45.&nbsp;&nbsp; &nbsp;В равностороннем треугольнике ABC проведена медиана AD. Найдите углы треугольника ABD.
+
45. В равностороннем треугольнике ABC проведена '''[[Высота, биссектриса и медиана треугольника. Полные уроки|медиана]]''' AD. Найдите углы треугольника ABD.  
-
46.&nbsp;&nbsp; &nbsp;Высоты треугольника ABC, проведенные из вершин А и С, пересекаются в точке М. Найдите [[Image:20-06-61.jpg]]AMC, если [[Image:20-06-61.jpg]]A = 70°[[Image:20-06-61.jpg]]C = 80°.
+
46. Высоты треугольника ABC, проведенные из вершин А и С, пересекаются в точке М. Найдите [[Image:20-06-61.jpg|Угол]]AMC, если [[Image:20-06-61.jpg|Угол]]A = 70°[[Image:20-06-61.jpg|Угол]]C = 80°.  
-
47*. В треугольнике ABC медиана BD равна половине стороны АС. Найдите угол В треугольника.
+
47*. В треугольнике ABC медиана BD равна половине стороны АС. Найдите угол В треугольника.  
-
48. Прямая а пересекает отрезок ВС в его середине. Докажите, что точки В и С находятся на одинаковом расстоянии от прямой а.
+
48. Прямая а пересекает отрезок ВС в его середине. Докажите, что точки В и С находятся на одинаковом расстоянии от прямой а.  
-
49.&nbsp;&nbsp; &nbsp;Отрезок ВС пересекает прямую а в точке О. Расстояния от точек В и С до прямой с равны. Докажите, что точка О является серединой отрезка ВС.
+
49. Отрезок ВС пересекает прямую а в точке О. Расстояния от точек В и С до прямой с равны. Докажите, что точка О является серединой отрезка ВС.  
-
50.&nbsp;&nbsp; &nbsp;Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.
+
50. Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.  
-
51.&nbsp;&nbsp; &nbsp;Докажите, что расстояния от вершин равностороннего треугольника до прямых, содержащих противолежащие им стороны, равны.
+
51. Докажите, что расстояния от вершин равностороннего треугольника до прямых, содержащих противолежащие им стороны, равны.  
-
<br>
+
<br>  
<br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>  
<br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>  
-
<sub>Материалы по математике за 7 класс [[Математика|скачать]], конспект по математике , учебники и книги скатать бесплатно, школьная программа [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>  
+
<br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub>  
<br>  
<br>  
  '''<u>Содержание урока</u>'''
  '''<u>Содержание урока</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока                      '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока                      '''
-
  [[Image:1236084776 kr.jpg|10x10px]] опорный каркас   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас   
-
  [[Image:1236084776 kr.jpg|10x10px]] презентация урока
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
-
  [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы  
-
  [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии  
   
   
  '''<u>Практика</u>'''
  '''<u>Практика</u>'''
-
  [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения  
-
  [[Image:1236084776 kr.jpg|10x10px]] самопроверка
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
-
  [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
-
  [[Image:1236084776 kr.jpg|10x10px]] домашние задания
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
-
  [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
-
  [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
-
 
+
  '''<u>Иллюстрации</u>'''
  '''<u>Иллюстрации</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
-
  [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки  
-
  [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
-
  [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
-
  [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
   
   
  '''<u>Дополнения</u>'''
  '''<u>Дополнения</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
-
  [[Image:1236084776 kr.jpg|10x10px]] статьи  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи  
-
  [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных  
-
  [[Image:1236084776 kr.jpg|10x10px]] шпаргалки  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки  
-
  [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
-
  [[Image:1236084776 kr.jpg|10x10px]] словарь терминов                           
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов                           
-
  [[Image:1236084776 kr.jpg|10x10px]] прочие  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие  
  '''<u></u>'''
  '''<u></u>'''
  <u>Совершенствование учебников и уроков
  <u>Совершенствование учебников и уроков
-
  </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
+
  </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
-
  [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике  
-
  [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке  
-
  [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми  
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми  
-
 
+
  '''<u>Только для учителей</u>'''
  '''<u>Только для учителей</u>'''
-
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
+
  <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
-
  [[Image:1236084776 kr.jpg|10x10px]] календарный план на год   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год   
-
  [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации   
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации   
-
  [[Image:1236084776 kr.jpg|10x10px]] программы
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
-
  [[Image:1236084776 kr.jpg|10x10px]] обсуждения
+
  [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
   
   
   
   

Текущая версия на 06:35, 18 июня 2012

Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Задачи-4(7 класс)


                                          Задачи


1. Докажите, что если некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Докажите, что если две прямые пересекаются, то любая третья прямая пересекает по крайней мере одну из этих прямых.

3. Дано: a||b||c||d. Докажите, что a||d.

4. Прямые АВ и CD параллельны. Докажите, что если отрезок ВС пересекает прямую AD, то точка пересечения принадлежит отрезку AD (см. рис. 70).

5. Дан треугольник ABC. На стороне АВ отмечена точка B1, а на стороне АС — точка С1(рис. 87). Назовите внутренние односторонние и внутренние накрест лежащие углы при прямых АВ, АС и секущей В1С1

6. Назовите внутренние накрест лежащие и внутренние односторонние углы на рисунке 72.

7. Отрезки AD и ВС пересекаются. Для прямых АС и BD и секущей ВС назовите пару внутренних накрест лежащих углов. Для тех же прямых и секущей АВ назовите пару внутренних односторонних углов. Объясните ответ.

8. Даны прямая АВ и точка С, не лежащая на этой прямой. Докажите, что через точку С можно провести прямзгю, параллельную прямой АВ. 9. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных параллельными и секущей, параллельны, т. е. лежат на параллельных прямых.

10. Отрезки АВ и CD пересекаются в точке Е и делятся этой точкой пополам. Докажите, что прямые АС и BD параллельны.

11. Треугольники ABC и BAD равны. Точки С и D лежат по разные стороны от прямой АВ. Докажите, что прямые АС и BD параллельны.

12. Угол ABC равен 80°, а угол BCD равен 120°. Могут ли прямые АВ и CD быть параллельными? Обоснуйте ответ.

13. Прямые АС и BD параллельны, причем точки А и D лежат по разные стороны от секущей ВС (рис. 77). Докажите, что:

1) углы DBC и АСВ внутренние накрест лежащие относительно секущей ВС;

2) луч ВС проходит между сторонами угла ABD;

3) углы CAB и DBA внутренние односторонние относительно секущей АВ.

14. 1) Разность двух внутренних односторонних углов при двух параллельных прямых и секущей равна 30°, Найдите эти углы.
2) Сумма двух внутренних накрест лежащих углов при двух параллельных прямых и секущей равна 150°. Чему равны эти углы?

15. Один из углов, которые получаются при пересечении двух параллельных прямых секущей, равен 72°. Найдите остальные семь углов.

16. Один из углов, которые получаются при пересечении двух параллельных прямых секущей, равен 30°. Может ли один из остальных семи углов равняться 70°? Объясните ответ.

17. Докажите, что две прямые, параллельные перпендикулярным прямым, сами перпендикулярны.

18. Найдите неизвестный угол треугольника, если у него два угла равны:

1) 50° и 30°; 2) 40° и 75°; 3) 65°и 80°; 4) 25° и 120°.

19. Найдите углы треугольника, если они пропорциональны числам:

1) 1, 2, 3;

2) 2, 3, 4;

3) 3, 4, 5;

4) 4, 5, 6;

5) 5, 6, 7.

20. Может ли в треугольнике быть:

1) два тупых угла;

2) тупой и прямой углы;

3) два прямых угла?

21. Может ли быть тупым угол при основании равнобедренного треугольника?

22. Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании у него равен:
1)    40°; 2) 55°; 3) 72°.

23. Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами равен:

1) 80°; 2) 120°; 3) 30°.

24. Один из углов равнобедренного треугольника равен 100°. Найдите остальные углы.

25. Один из углов равнобедренного треугольника равен 70°. Найдите остальные углы. Сколько решений имеет задача?

26. Докажите, что если один из углов равнобедренного треугольника равен 60°, то этот треугольник равносторонний.

27. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса CD. Найдите углы треугольника ABC, если угол ADC равен:

1) 60°; 2) 75°; 3) а.

28. В равнобедренном треугольнике AВС с основанием АС и углом при вершине В, равным 36°, проведена биссектриса AD. Докажите, что треугольники CDA и ADB равнобедренные (рис. 88).

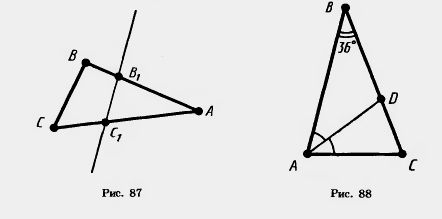
Треугольники


Треугольник 

29. В треугольнике ABC проведены биссектрисы из вершин А и В. Точка их пересечения обозначена D. Найдите угол ADB, если:

1) УголA = 50УголB= 100°;

2)УголA = a, УголB=b;

3) УголC = 130°;

4) УголC = y.

30. Чему равны углы равностороннего треугольника?

31. Под каким углом пересекаются биссектрисы двух внутренних односторонних углов при параллельных прямых?

32. Один из внешних углов равнобедренного треугольника равен 70°. Найдите углы треугольника.

33. Найдите углы треугольника, зная, что внешние углы при двух его вершинах равны 120° и 150°.

34. Два внешних угла треугольника равны 100° и 150°. Найдите третий внешний угол.

35. В треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими, если углы А тл В треугольника острые?

36. В треугольнике ABC проведена высота CD. Какая из трех точек А, В, D лежит между двумя другими, если угол А тупой? Обоснуйте ответ.

37. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.

38. Сумма внешних углов треугольника ABC при вершинах А и В, взятых по одному для каждой вершины, равна 240°. Чему равен угол С треугольника?

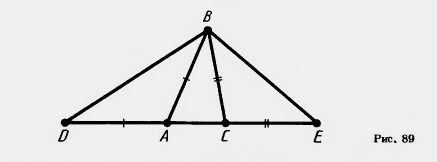
39. Дан треугольник ABC. На продолжении стороны АС отложены отрезки AD=AB и СЕ = СВ (рис. 89). Как найти углы треугольника DBE, зная углы треугольника АВС?

40. У треугольника один из внутренних углов равен 30°, а один из внешних 40°. Найдите остальные внутренние углы треугольника.

41. Из вершины прямого угла треугольника ABC проведена высота BD. Найдите угол CBD, зная, что:

1) УголA=20°; 2)Угол.A = 65°; 3) УголA=а.

42. Из вершины тупого угла В треугольника ABC проведена высота BD. Найдите углы треугольников ABD и CBD, зная, что УголA = a, УголB= в.

43. Докажите, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.

44. Найдите углы прямоугольного равнобедренного треугольника.

45. В равностороннем треугольнике ABC проведена медиана AD. Найдите углы треугольника ABD.

46. Высоты треугольника ABC, проведенные из вершин А и С, пересекаются в точке М. Найдите УголAMC, если УголA = 70°УголC = 80°.

47*. В треугольнике ABC медиана BD равна половине стороны АС. Найдите угол В треугольника.

48. Прямая а пересекает отрезок ВС в его середине. Докажите, что точки В и С находятся на одинаковом расстоянии от прямой а.

49. Отрезок ВС пересекает прямую а в точке О. Расстояния от точек В и С до прямой с равны. Докажите, что точка О является серединой отрезка ВС.

50. Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.

51. Докажите, что расстояния от вершин равностороннего треугольника до прямых, содержащих противолежащие им стороны, равны.



А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений



Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать 


Содержание урока
1236084776 kr.jpg конспект урока                       
1236084776 kr.jpg опорный каркас  
1236084776 kr.jpg презентация урока
1236084776 kr.jpg акселеративные методы 
1236084776 kr.jpg интерактивные технологии 

Практика
1236084776 kr.jpg задачи и упражнения 
1236084776 kr.jpg самопроверка
1236084776 kr.jpg практикумы, тренинги, кейсы, квесты
1236084776 kr.jpg домашние задания
1236084776 kr.jpg дискуссионные вопросы
1236084776 kr.jpg риторические вопросы от учеников

Иллюстрации
1236084776 kr.jpg аудио-, видеоклипы и мультимедиа 
1236084776 kr.jpg фотографии, картинки 
1236084776 kr.jpg графики, таблицы, схемы
1236084776 kr.jpg юмор, анекдоты, приколы, комиксы
1236084776 kr.jpg притчи, поговорки, кроссворды, цитаты

Дополнения
1236084776 kr.jpg рефераты
1236084776 kr.jpg статьи 
1236084776 kr.jpg фишки для любознательных 
1236084776 kr.jpg шпаргалки 
1236084776 kr.jpg учебники основные и дополнительные
1236084776 kr.jpg словарь терминов                          
1236084776 kr.jpg прочие 

Совершенствование учебников и уроков
1236084776 kr.jpg исправление ошибок в учебнике
1236084776 kr.jpg обновление фрагмента в учебнике 
1236084776 kr.jpg элементы новаторства на уроке 
1236084776 kr.jpg замена устаревших знаний новыми 

Только для учителей
1236084776 kr.jpg идеальные уроки 
1236084776 kr.jpg календарный план на год  
1236084776 kr.jpg методические рекомендации  
1236084776 kr.jpg программы
1236084776 kr.jpg обсуждения


Интегрированные уроки


Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-4(7_%D0%BA%D0%BB%D0%B0%D1%81%D1%81)»

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: