|
|
|
| (5 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Задачи-5(7 класс)</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Задачи, окружность, теорема, угол, прямая, равнобедренный треугольник, медиана</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Задачи-5(7 класс)''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 7 класс|Математика 7 класс]]>>Математика: Задачи-5(7 класс)''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ЗАДАЧИ '''<br><br>1. Докажите, что любой луч, исходящий из центра окружности, пересекает окружность в одной точке. | + | ''' Задачи '''<br><br>1. Докажите, что любой луч, исходящий из центра окружности, пересекает окружность в одной точке. |
| | | | |
| - | 2. Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках. | + | 2. Докажите, что прямая, проходящая через центр окружности, пересекает '''[[Окружность|окружность]]''' в двух точках. |
| | | | |
| - | 3. Докажите, что диаметр окружности, проходящий через середину хорды, перпендикулярен ей. | + | 3. Докажите, что диаметр окружности, проходящий через середину хорды, перпендикулярен ей. |
| | | | |
| - | 4. Сформулируйте и докажите теорему, обратную утверждению задачи 3. | + | 4. Сформулируйте и докажите '''[[Теоремы и доказательства. Полные уроки|теорему]]''', обратную утверждению задачи 3. |
| | | | |
| - | 5. 1) Из точки данной окружности проведены диаметр и хорда, равная радиусу. Найдите угол между ними (рис. 107). | + | 5. 1) Из точки данной окружности проведены диаметр и хорда, равная радиусу. Найдите '''[[Практикум на тему «Суміжні кути, їх властивості»|угол]]''' между ними (рис. 107). |
| | | | |
| | 2) Из точки данной окружности проведены две хорды, равные радиусу. Найдите угол между ними. | | 2) Из точки данной окружности проведены две хорды, равные радиусу. Найдите угол между ними. |
| Строка 19: |
Строка 19: |
| | <br> | | <br> |
| | | | |
| - | [[Image:21-06-52.jpg]] | + | [[Image:21-06-52.jpg|240px|Окружность]] |
| | | | |
| | <br>6. Докажите, что серединные перпендикуляры к двум сторонам треугольника пересекаются. | | <br>6. Докажите, что серединные перпендикуляры к двум сторонам треугольника пересекаются. |
| | | | |
| - | 7. Может ли окружность касаться прямой в двух точках? Объясните ответ. | + | 7. Может ли окружность касаться прямой в двух точках? Объясните ответ. |
| | | | |
| - | 8. Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. | + | 8. Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. |
| | | | |
| - | 9. Какие углы образует хорда АВ, равная радиусу окружности, с касательной в точке А? | + | 9. Какие углы образует хорда АВ, равная радиусу окружности, с касательной в точке А? |
| | | | |
| - | 10. Найдите углы, под которыми пересекаются прямые, касающиеся окружности в концах хорды, равной радиусу. | + | 10. Найдите углы, под которыми пересекаются прямые, касающиеся окружности в концах хорды, равной радиусу. |
| | | | |
| - | 11. Окружности с радиусами 30 см и 40 см касаются. Найдите расстояние между центрами окружностей в случаях внешнего и внутреннего касаний. | + | 11. Окружности с радиусами 30 см и 40 см касаются. Найдите расстояние между центрами окружностей в случаях внешнего и внутреннего касаний. |
| | | | |
| - | 12. Могут ли касаться две окружности, если их радиусы равны 25 см и 50 см, а расстояние между центрами 60 см? | + | 12. Могут ли касаться две окружности, если их радиусы равны 25 см и 50 см, а расстояние между центрами 60 см? |
| | | | |
| | 13*. 1) Точки А, В, С лежат на прямой, а точка О — вне прямой. Могут ли два треугольника АОВ и ВОС быть равнобедренными с основаниями АВ и ВС? Обоснуйте ответ. | | 13*. 1) Точки А, В, С лежат на прямой, а точка О — вне прямой. Могут ли два треугольника АОВ и ВОС быть равнобедренными с основаниями АВ и ВС? Обоснуйте ответ. |
| | | | |
| - | 2) Могут ли окружность и прямая пересекаться более чем в двух точках? | + | 2) Могут ли окружность и '''[[Точка и прямая|прямая]]''' пересекаться более чем в двух точках? |
| | | | |
| | 14*. 1) Окружности с центрами О и О<sub>1</sub> пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО<sub>1</sub> <br>2) Докажите, что две окружности не могут пересекаться более чем в двух точках. | | 14*. 1) Окружности с центрами О и О<sub>1</sub> пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО<sub>1</sub> <br>2) Докажите, что две окружности не могут пересекаться более чем в двух точках. |
| Строка 43: |
Строка 43: |
| | 15*. 1) Через точку А окружности с центром О проведена прямая, не касающаяся окружности. ОВ — перпендикуляр, опущенный на прямую. На продолжении отрезка АВ отложен отрезок ВС=АВ. Докажите, что точка С лежит на окружности. | | 15*. 1) Через точку А окружности с центром О проведена прямая, не касающаяся окружности. ОВ — перпендикуляр, опущенный на прямую. На продолжении отрезка АВ отложен отрезок ВС=АВ. Докажите, что точка С лежит на окружности. |
| | | | |
| - | 2) Докажите, что если прямая имеет с окружностью только одну общую точку, то она является касательной к окружности в этой точке. | + | 2) Докажите, что если прямая имеет с окружностью только одну общую точку, то она является касательной к окружности в этой точке. |
| | | | |
| - | 3) Докажите, что если две окружности имеют только одну общую точку, то они касаются в этой точке. | + | 3) Докажите, что если две окружности имеют только одну общую точку, то они касаются в этой точке. |
| | | | |
| - | 16*. 1) Из одной точки проведены две касательные к окружности (рис. 108). Докажите, что отрезки касательных MP и MQ равны.<br>2) Докажите, что через одну точку не может проходить больше двух касательных к окружности. | + | 16*. 1) Из одной точки проведены две касательные к окружности (рис. 108). Докажите, что отрезки касательных MP и MQ равны. |
| | + | |
| | + | 2) Докажите, что через одну точку не может проходить больше двух касательных к окружности. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:21-06-53.jpg]] | + | [[Image:21-06-53.jpg|480px|Касательная к окружности]] |
| | | | |
| | <br> | | <br> |
| | | | |
| - | 17. Одна окружность описана около равностороннего треугольника, а другая вписана в него. Докажите, что центры этих окружностей совпадают.<br> | + | 17. Одна окружность описана около равностороннего треугольника, а другая вписана в него. Докажите, что центры этих окружностей совпадают.<br> |
| | | | |
| - | 18. Окружность, вписанная в треугольник ABC, касается его сторон в точках А<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>(рис. 109). Докажите, что [[Image:21-06-54.jpg]]<br>19. Постройте треугольник по трем сторонам а, b и с:<br> | + | 18. Окружность, вписанная в треугольник ABC, касается его сторон в точках А<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>. Докажите, что центры этих окружностей совпадают.<br> |
| | | | |
| - | 1) а = 2 см, b = 3 см, с = 4 см;<br>
| + | 19. Постройте треугольник по трем сторонам а, b и с:<br> |
| | | | |
| - | 2) а = 3 см, b = 4 см, с = 5 см; <br>
| + | 1) а = 2 см, b = 3 см, с = 4 см;<br> |
| | | | |
| - | 3) а = 4 см, b = 5 см, с = 6 см.<br>
| + | 2) а = 3 см, b = 4 см, с = 5 см; <br> |
| | | | |
| - | 20. Дан треугольник ABC. Постройте другой, равный ему треугольник ABD.<br>
| + | 3) а = 4 см, b = 5 см, с = 6 см.<br> |
| | | | |
| - | 21. Постройте окружность данного радиуса, проходящую через две данные точки.<br>
| + | 20. Дан треугольник ABC. Постройте другой, равный ему треугольник ABD.<br> |
| | | | |
| - | 22. Постройте треугольник по двум сторонам и радиусу описанной окружности.<br>
| + | 21. Постройте окружность данного радиуса, проходящую через две данные точки.<br> |
| | | | |
| - | 23. Постройте треугольник ABC по следующим данным:<br>
| + | 22. Постройте треугольник по двум сторонам и радиусу описанной окружности.<br> |
| | | | |
| - | 1) по двум сторонам и углу между ними:<br>а) АВ = 5 см, АС = 6 см, А[[Image:20-06-61.jpg]]А = 40°;<br>б) АВ = 3 см, ВС = 5 см, [[Image:20-06-61.jpg]]В = 70°;<br>2) по стороне и прилежащим к ней углам:<br>а) АВ = 6 см, [[Image:20-06-61.jpg]]A = 30°, [[Image:20-06-61.jpg]]В = 50°;<br>б) АВ = 4 см, [[Image:20-06-61.jpg]]А = 45°, [[Image:20-06-61.jpg]]B=60°.<br>
| + | 23. Постройте треугольник ABC по следующим данным:<br> |
| | | | |
| - | 24. Постройте треугольник по двум сторонам и углу, противолежащему большей из них:<br>1) а = 6 см, Ь = 4 см. [[Image:21-06-55.jpg]] = 70°;<br>2) а = 4 см, Ь = 6 см. [[Image:21-06-56.jpg]]= 100°.<br>
| + | 1) по двум сторонам и углу между ними:<br>а) АВ = 5 см, АС = 6 см, А[[Image:20-06-61.jpg|Угол]]А = 40°;<br>б) АВ = 3 см, ВС = 5 см, [[Image:20-06-61.jpg|Угол]]В = 70°;<br>2) по стороне и прилежащим к ней углам:<br>а) АВ = 6 см, [[Image:20-06-61.jpg|Угол]]A = 30°, [[Image:20-06-61.jpg|Угол]]В = 50°;<br>б) АВ = 4 см, [[Image:20-06-61.jpg|Угол]]А = 45°, [[Image:20-06-61.jpg|Угол]]B=60°.<br> |
| | | | |
| - | 25. Постройте равнобедренный треугольник по боковой стороне и углу при основании.<br>
| + | 24. Постройте треугольник по двум сторонам и углу, противолежащему большей из них:<br>1) а = 6 см, Ь = 4 см. [[Image:21-06-55.jpg|Альфа]] = 70°;<br>2) а = 4 см, Ь = 6 см. [[Image:21-06-56.jpg|Бета]]= 100°.<br> |
| | | | |
| - | 26. Постройте окружность, вписанную в данный треугольник.<br>
| + | 25. Постройте '''[[Равнобедренный треугольник. Полные уроки|равнобедренный треугольник]]''' по боковой стороне и углу при основании.<br> |
| | | | |
| - | 27. Разделите угол на четыре равные части.<br>
| + | 26. Постройте окружность, вписанную в данный треугольник.<br> |
| | | | |
| - | 28. Постройте углы 60° и 30°.<br>
| + | 27. Разделите угол на четыре равные части.<br> |
| | | | |
| - | 29. Дан треугольник. Постройте его медианы.<br>
| + | 28. Постройте углы 60° и 30°.<br> |
| | | | |
| - | 30. Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.<br>
| + | 29. Дан треугольник. Постройте его медианы.<br> |
| | | | |
| - | 31. Постройте треугольник по стороне, медиане, проведенной к этой стороне, и радиусу описанной окружности.<br>
| + | 30. Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.<br> |
| | | | |
| - | 32. Постройте треугольник по двум сторонам и медиане, проведенной к третьей стороне (рис. 110).<br> <br>[[Image:21-06-57.jpg]]<br><br>33. Дан треугольник. Постройте его высоты. <br>34. Постройте окружность, описанную около данного треугольника.<br>
| + | 31. Постройте треугольник по стороне, медиане, проведенной к этой стороне, и радиусу описанной окружности.<br> |
| | | | |
| - | 35.Постройте прямоугольный треугольник по гипотенузе и катету.<br>
| + | 32. Постройте треугольник по двум сторонам и '''[[Высота, биссектриса и медиана треугольника. Полные уроки|медиане]]''', проведенной к третьей стороне (рис. 110).<br> <br>[[Image:21-06-57.jpg|480px|Треугольник и медиана]]<br><br>33. Дан треугольник. Постройте его высоты. <br>34. Постройте окружность, описанную около данного треугольника.<br> |
| | | | |
| - | 36. Постройте равнобедренный треугольник по боковой стороне и высоте, опущенной на основание.<br>
| + | 35.Постройте прямоугольный треугольник по гипотенузе и катету.<br> |
| | | | |
| - | 37. Постройте треугольник по двум сторонам и высоте, опущенной на третью сторону.<br>
| + | 36. Постройте равнобедренный треугольник по боковой стороне и высоте, опущенной на основание.<br> |
| | | | |
| - | 38. Постройте треугольник по двум сторонам и высоте, опущенной на одну из них.<br>
| + | 37. Постройте треугольник по двум сторонам и высоте, опущенной на третью сторону.<br> |
| | | | |
| - | 39.Постройте треугольник по стороне и проведенным к ней медиане и высоте.<br>
| + | 38. Постройте треугольник по двум сторонам и высоте, опущенной на одну из них.<br> |
| | | | |
| - | 40. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности.<br>
| + | 39.Постройте треугольник по стороне и проведенным к ней медиане и высоте.<br> |
| | | | |
| - | 41. Докажите, что геометрическое место точек, удаленных от данной прямой на расстояние h, состоит из двух прямых, параллельных данной и отстоящих от нее на h.<br>
| + | 40. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности.<br> |
| | | | |
| - | 42. На данной прямой найдите точку, которая находится на данном расстоянии от другой данной прямой.<br>
| + | 41. Докажите, что геометрическое место точек, удаленных от данной прямой на расстояние h, состоит из двух прямых, параллельных данной и отстоящих от нее на h.<br> |
| | | | |
| - | 43. Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В и находится на данном расстоянии от точки С.<br>
| + | 42. На данной прямой найдите точку, которая находится на данном расстоянии от другой данной прямой.<br> |
| | | | |
| - | 44. На данной прямой найдите точку, равноудаленную от двух данных точек.<br>
| + | 43. Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В и находится на данном расстоянии от точки С.<br> |
| | | | |
| - | 45. Даны четыре точки: А, В, С, D. Найдите точку X, которая одинаково удалена от точек А и В и одинаково удалена от точек С и D.<br>
| + | 44.На данной прямой найдите точку, равноудаленную от двух данных точек.<br> |
| | | | |
| - | 46*. Постройте треугольник, если заданы сторона, прилежащий к ней угол и сумма двух других сторон (рис. 111).<br> <br>[[Image:21-06-58.jpg]]<br><br>
| + | 45. Даны четыре точки: А, В, С, D. Найдите точку X, которая одинаково удалена от точек А и В и одинаково удалена от точек С и D.<br> |
| | | | |
| - | 47*. Постройте треугольник, если заданы сторона, прилежащий к ней угол и разность двух других сторон.<br>
| + | 46*. Постройте треугольник, если заданы сторона, прилежащий к ней угол и сумма двух других сторон (рис. 111).<br> <br>[[Image:21-06-58.jpg|480px|Треугольник]]<br><br> |
| | | | |
| - | 48*.Постройте прямоугольный треугольник по катету и сумме другого катета и гипотенузы.<br>
| + | 47*. Постройте треугольник, если заданы сторона, прилежащий к ней угол и разность двух других сторон.<br> |
| | | | |
| - | 49*. 1).Из точки А к окружности с центром О и радиусом R проведена касательная (рис.112). Докажите, что точка С касания лежит на основании равнобедренного треугольника ОАВ , у которого ОА=АВ, ОВ= 2R.<br>
| + | 48*.Постройте прямоугольный треугольник по катету и сумме другого катета и гипотенузы.<br> |
| | | | |
| - | 2). Проведите касательную к окружности, проходящую через данную точку вне окружности.
| + | 49*. 1).Из точки А к окружности с центром О и радиусом R проведена касательная (рис.112). Докажите, что точка С касания лежит на основании равнобедренного треугольника ОАВ , у которого ОА=АВ, ОВ= 2R.<br> |
| | | | |
| - | 50*. Проведите общую касательную к двум данным окружностям (рис.113)<br>
| + | 2). Проведите касательную к окружности, проходящую через данную точку вне окружности. |
| | | | |
| | + | 50*. Проведите общую касательную к двум данным окружностям (рис.113)<br> |
| | | | |
| | + | <br> |
| | | | |
| - | [[Image:21-06-59.jpg]] | + | [[Image:21-06-59.jpg|480px|Касательная к окружности]] |
| - | | + | |
| | | | |
| | + | <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | [http://xvatit.com/relax/fun-videos/ '''<sub>Видео</sub>''']<sub>по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | | | |
| | <br> | | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 11:36, 18 июня 2012
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Задачи-5(7 класс)
Задачи
1. Докажите, что любой луч, исходящий из центра окружности, пересекает окружность в одной точке.
2. Докажите, что прямая, проходящая через центр окружности, пересекает окружность в двух точках.
3. Докажите, что диаметр окружности, проходящий через середину хорды, перпендикулярен ей.
4. Сформулируйте и докажите теорему, обратную утверждению задачи 3.
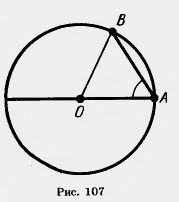
5. 1) Из точки данной окружности проведены диаметр и хорда, равная радиусу. Найдите угол между ними (рис. 107).
2) Из точки данной окружности проведены две хорды, равные радиусу. Найдите угол между ними.
6. Докажите, что серединные перпендикуляры к двум сторонам треугольника пересекаются.
7. Может ли окружность касаться прямой в двух точках? Объясните ответ.
8. Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания.
9. Какие углы образует хорда АВ, равная радиусу окружности, с касательной в точке А?
10. Найдите углы, под которыми пересекаются прямые, касающиеся окружности в концах хорды, равной радиусу.
11. Окружности с радиусами 30 см и 40 см касаются. Найдите расстояние между центрами окружностей в случаях внешнего и внутреннего касаний.
12. Могут ли касаться две окружности, если их радиусы равны 25 см и 50 см, а расстояние между центрами 60 см?
13*. 1) Точки А, В, С лежат на прямой, а точка О — вне прямой. Могут ли два треугольника АОВ и ВОС быть равнобедренными с основаниями АВ и ВС? Обоснуйте ответ.
2) Могут ли окружность и прямая пересекаться более чем в двух точках?
14*. 1) Окружности с центрами О и О1 пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО1
2) Докажите, что две окружности не могут пересекаться более чем в двух точках.
15*. 1) Через точку А окружности с центром О проведена прямая, не касающаяся окружности. ОВ — перпендикуляр, опущенный на прямую. На продолжении отрезка АВ отложен отрезок ВС=АВ. Докажите, что точка С лежит на окружности.
2) Докажите, что если прямая имеет с окружностью только одну общую точку, то она является касательной к окружности в этой точке.
3) Докажите, что если две окружности имеют только одну общую точку, то они касаются в этой точке.
16*. 1) Из одной точки проведены две касательные к окружности (рис. 108). Докажите, что отрезки касательных MP и MQ равны.
2) Докажите, что через одну точку не может проходить больше двух касательных к окружности.
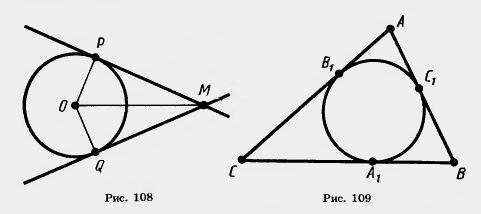
17. Одна окружность описана около равностороннего треугольника, а другая вписана в него. Докажите, что центры этих окружностей совпадают.
18. Окружность, вписанная в треугольник ABC, касается его сторон в точках А1, В1, С1. Докажите, что центры этих окружностей совпадают.
19. Постройте треугольник по трем сторонам а, b и с:
1) а = 2 см, b = 3 см, с = 4 см;
2) а = 3 см, b = 4 см, с = 5 см;
3) а = 4 см, b = 5 см, с = 6 см.
20. Дан треугольник ABC. Постройте другой, равный ему треугольник ABD.
21. Постройте окружность данного радиуса, проходящую через две данные точки.
22. Постройте треугольник по двум сторонам и радиусу описанной окружности.
23. Постройте треугольник ABC по следующим данным:
1) по двум сторонам и углу между ними:
а) АВ = 5 см, АС = 6 см, А А = 40°; А = 40°;
б) АВ = 3 см, ВС = 5 см,  В = 70°; В = 70°;
2) по стороне и прилежащим к ней углам:
а) АВ = 6 см,  A = 30°, A = 30°,  В = 50°; В = 50°;
б) АВ = 4 см,  А = 45°, А = 45°,  B=60°. B=60°.
24. Постройте треугольник по двум сторонам и углу, противолежащему большей из них:
1) а = 6 см, Ь = 4 см. 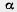 = 70°; = 70°;
2) а = 4 см, Ь = 6 см. 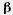 = 100°. = 100°.
25. Постройте равнобедренный треугольник по боковой стороне и углу при основании.
26. Постройте окружность, вписанную в данный треугольник.
27. Разделите угол на четыре равные части.
28. Постройте углы 60° и 30°.
29. Дан треугольник. Постройте его медианы.
30. Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.
31. Постройте треугольник по стороне, медиане, проведенной к этой стороне, и радиусу описанной окружности.
32. Постройте треугольник по двум сторонам и медиане, проведенной к третьей стороне (рис. 110).
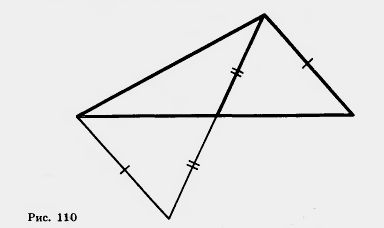
33. Дан треугольник. Постройте его высоты.
34. Постройте окружность, описанную около данного треугольника.
35.Постройте прямоугольный треугольник по гипотенузе и катету.
36. Постройте равнобедренный треугольник по боковой стороне и высоте, опущенной на основание.
37. Постройте треугольник по двум сторонам и высоте, опущенной на третью сторону.
38. Постройте треугольник по двум сторонам и высоте, опущенной на одну из них.
39.Постройте треугольник по стороне и проведенным к ней медиане и высоте.
40. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности.
41. Докажите, что геометрическое место точек, удаленных от данной прямой на расстояние h, состоит из двух прямых, параллельных данной и отстоящих от нее на h.
42. На данной прямой найдите точку, которая находится на данном расстоянии от другой данной прямой.
43. Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В и находится на данном расстоянии от точки С.
44.На данной прямой найдите точку, равноудаленную от двух данных точек.
45. Даны четыре точки: А, В, С, D. Найдите точку X, которая одинаково удалена от точек А и В и одинаково удалена от точек С и D.
46*. Постройте треугольник, если заданы сторона, прилежащий к ней угол и сумма двух других сторон (рис. 111).
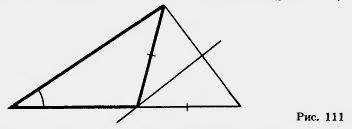
47*. Постройте треугольник, если заданы сторона, прилежащий к ней угол и разность двух других сторон.
48*.Постройте прямоугольный треугольник по катету и сумме другого катета и гипотенузы.
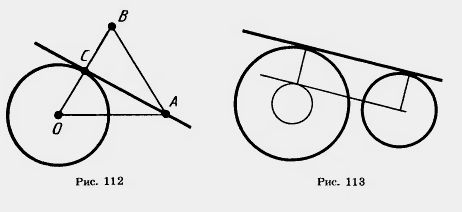
49*. 1).Из точки А к окружности с центром О и радиусом R проведена касательная (рис.112). Докажите, что точка С касания лежит на основании равнобедренного треугольника ОАВ , у которого ОА=АВ, ОВ= 2R.
2). Проведите касательную к окружности, проходящую через данную точку вне окружности.
50*. Проведите общую касательную к двум данным окружностям (рис.113)
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видеопо математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|















