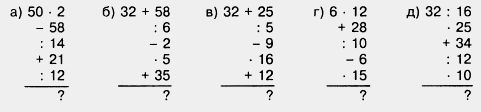|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Формулы</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Формулы, число, уравнение, задачи, выражение, километров, формуле, периметр, квадраты чисел</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Формулы''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Формулы'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br> | + | '''Формулы '''<br> |
| | | | |
| - | '''Формулы '''<br>
| + | <br>'''Задача 1'''. Велосипедист едет со скоростью 15 км/ч. Какое расстояние он проедет за 4 ч? |
| | | | |
| - | <br>'''Задача 1'''. Велосипедист едет со скоростью 15 км/ч. Какое расстояние он проедет за 4 ч? <br>Решение. Чтобы узнать, сколько километров проедет велосипедист, надо умножить его скорость на время пути, то есть найти произведение 15-4. <br>Получаем, что путь равен 60 км. <br>Запишем правило нахождения пути по скорости и времени движения в буквенном виде. Обозначим путь буквой s, скорость — буквой v и время — <br>буквой t. Получим равенство s = vt. <br>Это равенство называют '''формулой пути'''. <br>Запись какого-нибудь правила с помощью букв называют '''формулой'''. <br>По формуле пути можно решать различные задачи.
| + | '''Решение'''. Чтобы узнать, сколько '''[[Міри довжини. Кілометр. Порівняння значень величин|километров]]''' проедет велосипедист, надо умножить его скорость на время пути, то есть найти произведение 15-4. Получаем, что путь равен 60 км. |
| | | | |
| - | '''Задача 2.''' Автомобиль движется со скоростью 60 км/ч. За какое время он пройдет путь в 600 км? <br>Решение. Заменим в формуле s = vt буквы s и v их значениями: s = 600, v = 60.
| + | Запишем правило нахождения пути по скорости и времени движения в буквенном виде. Обозначим путь буквой s, скорость — буквой v и время — буквой t. Получим равенство s = vt. |
| | | | |
| - | Получим уравнение: 600 = 60t. <br>Из него находим, что t = 600 : 60, то есть t = 10. Значит, чтобы проехать 600 км, автомобиль должен двигаться 10 ч.
| + | ''Это равенство называют формулой пути. '' |
| | | | |
| - | [[Image:16-06-6.jpg]]<br><br>'''Задача 3.''' С какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч? <br>Решение. Заменим в формуле s = vt буквы s и t их значениями: s = 24, t = 4. Получим уравнение: 24 = v • 4, то есть 24 = 4v. Решив уравнение, получим:
| + | ''Запись какого-нибудь правила с помощью букв называют формулой. '' |
| | | | |
| - | v = 6. Значит, человек должен идти со скоростью 6 км/ч. <br>
| + | По формуле пути можно решать различные '''[[Практичне завдання до теми Додавання та віднімання чисел в межах 10 Поняття вартість монет|задачи]]'''. |
| | | | |
| - | '''Запишите формулу пути и расскажите, что означают входящие в нее буквы.''' | + | '''Задача 2.''' Автомобиль движется со скоростью 60 км/ч. За какое время он пройдет путь в 600 км? <br>'''Решение'''. Заменим в формуле s = vt буквы s и v их значениями: s = 600, v = 60. |
| | + | |
| | + | Получим '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''': 600 = 60t. |
| | + | |
| | + | Из него находим, что t = 600 : 60, то есть t = 10. Значит, чтобы проехать 600 км, автомобиль должен двигаться 10 ч. |
| | + | |
| | + | [[Image:16-06-6.jpg|120px|Задание]]<br><br>'''Задача 3.''' С какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч? |
| | + | |
| | + | '''Решение'''. Заменим в формуле s = vt буквы s и t их значениями: s = 24, t = 4. Получим уравнение: 24 = v • 4, то есть 24 = 4v. Решив уравнение, получим: v = 6. Значит, человек должен идти со скоростью 6 км/ч. <br> |
| | + | |
| | + | ''Запишите формулу пути и расскажите, что означают входящие в нее буквы.'' |
| | | | |
| | 674. Найдите по формуле s = vt путь, пройденный: <br>а) со скоростью 96 м/мин за 25 мин; <br>б) со скоростью 7 км/ч за 6 ч. | | 674. Найдите по формуле s = vt путь, пройденный: <br>а) со скоростью 96 м/мин за 25 мин; <br>б) со скоростью 7 км/ч за 6 ч. |
| | | | |
| - | 675. Найдите по формуле пути значение скорости v если: <br>а) t = 12 ч, s = 240 км; <br>б) t = 5 с, s = 15 м. <br> | + | 675. Найдите по '''[[Фішки для допитливих до уроку на тему «Величина. Числові і буквені вирази, їх числове значення. Формули»|формуле]]''' пути значение скорости v если: |
| | | | |
| - | 676. Найдите по формуле пути значение времени t, если: <br>а) s = 64 км, и = 8 км/с; <br>б) s = 132 км, v = 12 км/ч. <br>
| + | а) t = 12 ч, s = 240 км; <br>б) t = 5 с, s = 15 м. <br> |
| | | | |
| - | 677. Запишите формулу для вычисления периметра прямоугольника, если буквами а и b обозначены длины сторон прямоугольника, а буквой Р <br>его периметр. Вычислите по этой формуле: <br>а) периметр Р прямоугольника, если его стороны а = 4 дм и b = 3 дм; <br>б) сторону прямоугольника, если его периметр равен 30 см, а другая сторона — 7 см. <br>
| + | 676. Найдите по формуле пути значение времени t, если: |
| | | | |
| - | 678. Запишите формулу для вычисления периметра Р квадрата, сторона которого а. Вычислите по этой формуле: <br>а) периметр квадрата со стороной 9 см; <br>б) сторону квадрата, периметр которого 64 м. <br>
| + | а) s = 64 км, и = 8 км/с; <br>б) s = 132 км, v = 12 км/ч. <br> |
| | | | |
| - | 679. Запишите в виде формулы правило нахождения делимого а по делителю b, неполному частному q и остатку r. По этой формуле найдите: <br>а) делимое а, если неполное частное равно 15, делитель — 7 и остаток — 4; <br>б) делитель b, если а = 257, q = 28, r = 5; <br>в) неполное частное q, если а = 597, b = 12, r = 9. <br>
| + | 677. Запишите формулу для вычисления периметра прямоугольника, если буквами а и b обозначены длины сторон прямоугольника, а буквой Р его периметр. Вычислите по этой формуле: |
| | | | |
| - | 680. С одной станции в противоположных направлениях вышли два поезда в одно и то же время. Скорость одного поезда 50 км/ч, а скорость другого поезда 70 км/ч. Какое расстояние будет между ними через t часов после отправления в путь? Запишите ответ в виде формулы и упростите ее. Что означает число 120 в получившейся формуле? <br>
| + | а) '''[[Прямокутник, квадрат, їх периметри. Презентація уроку|периметр]]''' Р прямоугольника, если его стороны а = 4 дм и b = 3 дм; <br>б) сторону прямоугольника, если его периметр равен 30 см, а другая сторона — 7 см. <br> |
| | | | |
| - | 681. Расстояние между двумя городами 600 км. Навстречу друг другу из этих городов вышли одновременно две автомашины. Одна имеет скорость 60 км/ч, а другая — 40 км/ч. Чему равно расстояние между машинами через t часов после выезда? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 100 в получившейся формуле? <br>
| + | 678. Запишите формулу для вычисления периметра Р квадрата, сторона которого а. Вычислите по этой формуле: |
| | | | |
| - | 682. Первая черепаха догоняет вторую. Скорость первой черепахи 130 см в минуту, а скорость второй — 97 см в минуту. Сейчас расстояние между ними 198 см. Чему будет равно расстояние между черепахами через t мин? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 33 в этой формуле? Через сколько минут первая черепаха догонит вторую? <br>
| + | а) периметр квадрата со стороной 9 см; <br>б) сторону квадрата, периметр которого 64 м. <br> |
| | | | |
| - | 683. Расстояние между селами Ивановка и Дятьково равно 90 км. Из Ивановки в Дятьково выехал велосипедист со скоростью 10 км/ч. Наишите формулу, выражающую расстояние s от велосипедиста до Дятьково через t часов после его выезда. <br>
| + | 679. Запишите в виде формулы правило нахождения делимого а по делителю b, неполному частному q и остатку r. По этой формуле найдите: |
| | | | |
| - | 684. Вычислите устно: <br>
| + | а) делимое а, если неполное частное равно 15, делитель — 7 и остаток — 4; <br>б) делитель b, если а = 257, q = 28, r = 5; <br>в) неполное частное q, если а = 597, b = 12, r = 9. <br> |
| | | | |
| - | [[Image:16-06-7.jpg]]<br><br>685. Восстановите цепочку вычислений: <br> | + | 680. С одной станции в противоположных направлениях вышли два поезда в одно и то же время. Скорость одного поезда 50 км/ч, а скорость другого поезда 70 км/ч. Какое расстояние будет между ними через t часов после отправления в путь? Запишите ответ в виде формулы и упростите ее. Что означает '''[[Додавання і віднімання натуральних чисел|число]]''' 120 в получившейся формуле? <br> |
| | | | |
| - | [[Image:16-06-8.jpg]]<br><br>686. Найдите квадраты чисел 2; 5; 7; 8; 10; 20. Найдите кубы чисел 2; 3; 5; 10; 30. <br>
| + | 681. Расстояние между двумя городами 600 км. Навстречу друг другу из этих городов вышли одновременно две автомашины. Одна имеет скорость 60 км/ч, а другая — 40 км/ч. Чему равно расстояние между машинами через t часов после выезда? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 100 в получившейся формуле? <br> |
| | | | |
| - | 687. Квадрат какого числа равен 4; 16; 36; 81; 900? Куб какого числа равен 1; 8; 64; 125; 27 000? <br>
| + | 682. Первая черепаха догоняет вторую. Скорость первой черепахи 130 см в минуту, а скорость второй — 97 см в минуту. Сейчас расстояние между ними 198 см. Чему будет равно расстояние между черепахами через t мин? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 33 в этой формуле? Через сколько минут первая черепаха догонит вторую? <br> |
| | | | |
| - | 688. Вычислите наиболее простым способом: <br>
| + | 683. Расстояние между селами Ивановка и Дятьково равно 90 км. Из Ивановки в Дятьково выехал велосипедист со скоростью 10 км/ч. Наишите формулу, выражающую расстояние s от велосипедиста до Дятьково через t часов после его выезда. <br> |
| | | | |
| - | а) 4 • 19 • 25; г) 50 • 75 • 2; <br>б) 8 • 15 • 125; д) 16 • 47 • 125; <br>в) 250 • 35 • 8; е) 40 • 8 • 25 • 125. <br>
| + | 684. Вычислите устно: <br> |
| | | | |
| - | 689. Изменится ли частное двух чисел, если: <br>
| + | [[Image:16-06-7.jpg|480px|Задание]]<br><br>685. Восстановите цепочку вычислений: <br> |
| | | | |
| - | а) делимое увеличить в 2 раза; в 3 раза; <br>б) делимое и делитель увеличить в одинаковое число раз? <br>Приведите примеры. <br>
| + | [[Image:16-06-8.jpg|480px|Задание]]<br><br>686. Найдите '''[[Множення натуральних чисел. Квадрат і куб числа. Презентація уроку|квадраты чисел]]''' 2; 5; 7; 8; 10; 20. Найдите кубы чисел 2; 3; 5; 10; 30. <br> |
| | | | |
| - | 690. Расскажите, в каком порядке надо выполнять действия при нахождении значения выражения: <br>
| + | 687. Квадрат какого числа равен 4; 16; 36; 81; 900? Куб какого числа равен 1; 8; 64; 125; 27 000? <br> |
| | | | |
| - | а) 23 • 82- 15 • 33+ 1734 : 17; <br>б) 5 • 113-4 • (76 + 132- 5). <br>
| + | 688. Вычислите наиболее простым способом: <br> |
| | | | |
| - | 691. Попробуйте найти число, квадрат которого оканчивается цифрой 0; 6; 5; 7.Какой цифрой может оканчиваться квадрат числа? куб числа? <br>692. Машина двигалась 4 ч со скоростью а км/ч и 3 ч со скоростью b км/ч. Какой путь прошла машина за эти 7 часов? <br>Составьте выражение для решения задачи и найдите его значение при: <br>а = 40, b = 30; а = 30, b = 40; а = 60, b = 70. | + | а) 4 • 19 • 25; г) 50 • 75 • 2; <br>б) 8 • 15 • 125; д) 16 • 47 • 125; <br>в) 250 • 35 • 8; е) 40 • 8 • 25 • 125. <br> |
| | + | |
| | + | 689. Изменится ли частное двух чисел, если: <br> |
| | + | |
| | + | а) делимое увеличить в 2 раза; в 3 раза; <br>б) делимое и делитель увеличить в одинаковое число раз? |
| | + | |
| | + | Приведите примеры. <br> |
| | + | |
| | + | 690. Расскажите, в каком порядке надо выполнять действия при нахождении значения выражения: <br> |
| | + | |
| | + | а) 23 • 82- 15 • 33+ 1734 : 17; <br>б) 5 • 113-4 • (76 + 132- 5). <br> |
| | + | |
| | + | 691. Попробуйте найти число, квадрат которого оканчивается цифрой 0; 6; 5; 7.Какой цифрой может оканчиваться квадрат числа? куб числа? |
| | + | |
| | + | 692. Машина двигалась 4 ч со скоростью а км/ч и 3 ч со скоростью b км/ч. Какой путь прошла машина за эти 7 часов? |
| | + | |
| | + | Составьте '''[[Повторення таблиць додавання і віднімання. Складання виразів за текстовим формулюванням|выражение]]''' для решения задачи и найдите его значение при: |
| | + | |
| | + | а = 40, b = 30; а = 30, b = 40; а = 60, b = 70. |
| | | | |
| | 693. Найдите значение выражения: | | 693. Найдите значение выражения: |
| | | | |
| - | а) З2 + 42; в) (92 - 42) : (9 - 4); <br>б) (42 + 1)2; г) (83 + 73) : (82 - 72). | + | а) З2 + 42; в) (92 - 42) : (9 - 4); <br>б) (42 + 1)2; г) (83 + 73) : (82 - 72). |
| | | | |
| - | 694. Семье, состоящей из бабушки, папы, мамы, дочери и сына, подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами <br>семьи? <br>Решение. У первого члена семьи (например, бабушки) есть 5 вариантов выбора, у следующего (пусть это будет папа) остается 4 варианта выбора, следующий (например, мама) будет выбирать уже из 3 чашек, следующий — из двух, последний же получает одну оставшуюся чашку. Покажем эти <br>способы на схеме. | + | 694. Семье, состоящей из бабушки, папы, мамы, дочери и сына, подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи? |
| | | | |
| - | [[Image:16-06-9.jpg]]<br><br>Получили, что каждому выбору чашки бабушкой соответствует четыре возможных выбора папы, т. е. всего 5 • 4 способов. После того как папа выбрал <br>чашку, у мамы есть три варианта выбора, у дочери — два, у сына — один, т. е. всего 3-2-1 способов. Окончательно получаем, что для решения задачи <br>надо найти произведение 5 • 4 • 3 • 2 -1. Заметим, что получили произведение всех натуральных чисел от 1 до 5. Такие произведения записывают короче:
| + | '''Решение'''. У первого члена семьи (например, бабушки) есть 5 вариантов выбора, у следующего (пусть это будет папа) остается 4 варианта выбора, следующий (например, мама) будет выбирать уже из 3 чашек, следующий — из двух, последний же получает одну оставшуюся чашку. Покажем эти способы на [http://xvatit.com/it/fishki-ot-itshki/ '''схеме''']. |
| | | | |
| - | 5 • 4 • 3 • 2 • 1 = 5! (читают: «пять факториал»). <br>Итак, ответ задачи: 5! = 120, т. е. чашки между членами семьи можно распределить ста двадцатью способами.
| + | [[Image:16-06-9.jpg|550px|Задание]]<br><br>Получили, что каждому выбору чашки бабушкой соответствует четыре возможных выбора папы, т. е. всего 5 • 4 способов. После того как папа выбрал чашку, у мамы есть три варианта выбора, у дочери — два, у сына — один, т. е. всего 3-2-1 способов. Окончательно получаем, что для решения задачи надо найти произведение 5 • 4 • 3 • 2 -1. Заметим, что получили произведение всех натуральных чисел от 1 до 5. Такие произведения записывают короче: |
| | | | |
| - | 695. Толя начал читать книгу, когда Сережа прочитал уже 24 страницы такой же книги. Догонит ли Толя Сережу через 5 дней, если будет читать в день — <br>18 страниц, а Сережа — 12? | + | 5 • 4 • 3 • 2 • 1 = 5! (читают: «пять факториал»). |
| | + | |
| | + | Итак, ответ задачи: 5! = 120, т. е. чашки между членами семьи можно распределить ста двадцатью способами. |
| | + | |
| | + | 695. Толя начал читать книгу, когда Сережа прочитал уже 24 страницы такой же книги. Догонит ли Толя Сережу через 5 дней, если будет читать в день — 18 страниц, а Сережа — 12? |
| | | | |
| | 696. Начертите координатный луч. Отметьте на нем точки А(5), В(7), С(0) и 0(3). Чему равна длина (в единичных отрезках) отрезков АВ, CD, AD? | | 696. Начертите координатный луч. Отметьте на нем точки А(5), В(7), С(0) и 0(3). Чему равна длина (в единичных отрезках) отрезков АВ, CD, AD? |
| Строка 79: |
Строка 111: |
| | 697. Через точки Р и К проведите прямую и отметьте на ней точки С и D так, чтобы точка D лежала между Р и /С, а точка Р — между С и D. | | 697. Через точки Р и К проведите прямую и отметьте на ней точки С и D так, чтобы точка D лежала между Р и /С, а точка Р — между С и D. |
| | | | |
| - | 698. Докажите, что: <br>а) 600 < 23 • 35 < 1200; | + | 698. Докажите, что: |
| | + | |
| | + | а) 600 < 23 • 35 < 1200; |
| | | | |
| | б) 2400 < 47 • 62 < 3500. | | б) 2400 < 47 • 62 < 3500. |
| | | | |
| - | 699. Решите задачу: <br>1) Бронза содержит (по массе) 41 часть меди, 8 частей олова и 1 часть цинка. Какова масса куска бронзы, если в ней олова меньше, чем меди, на 132 г? <br>2) Дюралюминий — сплав, состоящий из 83 частей алюминия, 5 частей меди, 1 части марганца и 1 части магния (по массе). Какова масса куска дюралюминия, если в нем меди больше, чем магния, на 84 г? | + | 699. Решите задачу: |
| | | | |
| - | 700. Массу М товара с упаковкой (ее называют массой брутто) определяют так: вычисляют массу товара (она называется массой нетто) и прибавляют к ней массу р упаковки. Запишите это правило в виде формулы, если масса одного изделия т и в упаковке п изделий. Найдите по этой формуле массу брутто ящика чая, в котором 50 пачек чая, по 100 г каждая, а масса ящика 1 кг.
| + | 1) Бронза содержит (по массе) 41 часть меди, 8 частей олова и 1 часть цинка. Какова масса куска бронзы, если в ней олова меньше, чем меди, на 132 г? |
| | | | |
| - | 701. Найдите по формуле пути: <br>а) значение s, если v = 12 км/ч, t — 3 ч; <br>б) значение t, если s = 180 м, v = 15 м/с. | + | 2) Дюралюминий — сплав, состоящий из 83 частей алюминия, 5 частей меди, 1 части марганца и 1 части магния (по массе). Какова масса куска дюралюминия, если в нем меди больше, чем магния, на 84 г? |
| | + | |
| | + | 700. Массу М товара с упаковкой (ее называют массой брутто) определяют так: вычисляют массу товара (она называется массой нетто) и прибавляют к ней массу р упаковки. Запишите это правило в виде формулы, если масса одного изделия т и в упаковке n изделий. Найдите по этой формуле массу брутто ящика чая, в котором 50 пачек чая, по 100 г каждая, а масса ящика 1 кг. |
| | + | |
| | + | 701. Найдите по формуле пути: |
| | + | |
| | + | а) значение s, если v = 12 км/ч, t — 3 ч; <br>б) значение t, если s = 180 м, v = 15 м/с. |
| | | | |
| | 702. Найдите по формуле для нахождения периметра прямоугольника: | | 702. Найдите по формуле для нахождения периметра прямоугольника: |
| Строка 103: |
Строка 143: |
| | 707. Решите уравнение: | | 707. Решите уравнение: |
| | | | |
| - | а) (Зх + bх) • 18 = 144; <br>б) (7у - Зу) : 8 = 17; | + | а) (Зх + bх) • 18 = 144; <br>б) (7у - Зу) : 8 = 17; |
| | | | |
| - | в) (6а + а) : 13 = 14; <br>г) 48 : (9b - b) = 2. | + | в) (6а + а) : 13 = 14; <br>г) 48 : (9b - b) = 2. |
| | | | |
| | 708. Выполните действия: | | 708. Выполните действия: |
| | | | |
| - | а) 183 340 : 89 • 104; <br>б) 102 720 : 96 • 203. <br><br> | + | а) 183 340 : 89 • 104; <br>б) 102 720 : 96 • 203. |
| | | | |
| | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | + | |
| | + | |
| | | | |
| | <sub>Математика для 5 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Математика для 5 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 118: |
Строка 160: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 09:00, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Формулы
Формулы
Задача 1. Велосипедист едет со скоростью 15 км/ч. Какое расстояние он проедет за 4 ч?
Решение. Чтобы узнать, сколько километров проедет велосипедист, надо умножить его скорость на время пути, то есть найти произведение 15-4. Получаем, что путь равен 60 км.
Запишем правило нахождения пути по скорости и времени движения в буквенном виде. Обозначим путь буквой s, скорость — буквой v и время — буквой t. Получим равенство s = vt.
Это равенство называют формулой пути.
Запись какого-нибудь правила с помощью букв называют формулой.
По формуле пути можно решать различные задачи.
Задача 2. Автомобиль движется со скоростью 60 км/ч. За какое время он пройдет путь в 600 км?
Решение. Заменим в формуле s = vt буквы s и v их значениями: s = 600, v = 60.
Получим уравнение: 600 = 60t.
Из него находим, что t = 600 : 60, то есть t = 10. Значит, чтобы проехать 600 км, автомобиль должен двигаться 10 ч.

Задача 3. С какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч?
Решение. Заменим в формуле s = vt буквы s и t их значениями: s = 24, t = 4. Получим уравнение: 24 = v • 4, то есть 24 = 4v. Решив уравнение, получим: v = 6. Значит, человек должен идти со скоростью 6 км/ч.
Запишите формулу пути и расскажите, что означают входящие в нее буквы.
674. Найдите по формуле s = vt путь, пройденный:
а) со скоростью 96 м/мин за 25 мин;
б) со скоростью 7 км/ч за 6 ч.
675. Найдите по формуле пути значение скорости v если:
а) t = 12 ч, s = 240 км;
б) t = 5 с, s = 15 м.
676. Найдите по формуле пути значение времени t, если:
а) s = 64 км, и = 8 км/с;
б) s = 132 км, v = 12 км/ч.
677. Запишите формулу для вычисления периметра прямоугольника, если буквами а и b обозначены длины сторон прямоугольника, а буквой Р его периметр. Вычислите по этой формуле:
а) периметр Р прямоугольника, если его стороны а = 4 дм и b = 3 дм;
б) сторону прямоугольника, если его периметр равен 30 см, а другая сторона — 7 см.
678. Запишите формулу для вычисления периметра Р квадрата, сторона которого а. Вычислите по этой формуле:
а) периметр квадрата со стороной 9 см;
б) сторону квадрата, периметр которого 64 м.
679. Запишите в виде формулы правило нахождения делимого а по делителю b, неполному частному q и остатку r. По этой формуле найдите:
а) делимое а, если неполное частное равно 15, делитель — 7 и остаток — 4;
б) делитель b, если а = 257, q = 28, r = 5;
в) неполное частное q, если а = 597, b = 12, r = 9.
680. С одной станции в противоположных направлениях вышли два поезда в одно и то же время. Скорость одного поезда 50 км/ч, а скорость другого поезда 70 км/ч. Какое расстояние будет между ними через t часов после отправления в путь? Запишите ответ в виде формулы и упростите ее. Что означает число 120 в получившейся формуле?
681. Расстояние между двумя городами 600 км. Навстречу друг другу из этих городов вышли одновременно две автомашины. Одна имеет скорость 60 км/ч, а другая — 40 км/ч. Чему равно расстояние между машинами через t часов после выезда? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 100 в получившейся формуле?
682. Первая черепаха догоняет вторую. Скорость первой черепахи 130 см в минуту, а скорость второй — 97 см в минуту. Сейчас расстояние между ними 198 см. Чему будет равно расстояние между черепахами через t мин? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 33 в этой формуле? Через сколько минут первая черепаха догонит вторую?
683. Расстояние между селами Ивановка и Дятьково равно 90 км. Из Ивановки в Дятьково выехал велосипедист со скоростью 10 км/ч. Наишите формулу, выражающую расстояние s от велосипедиста до Дятьково через t часов после его выезда.
684. Вычислите устно:
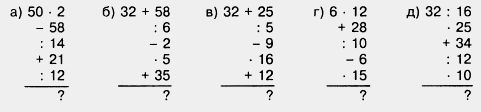
685. Восстановите цепочку вычислений:
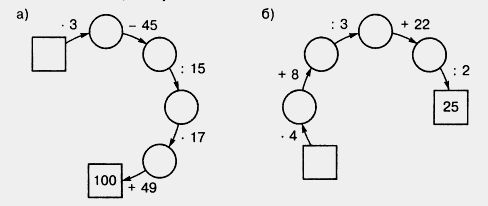
686. Найдите квадраты чисел 2; 5; 7; 8; 10; 20. Найдите кубы чисел 2; 3; 5; 10; 30.
687. Квадрат какого числа равен 4; 16; 36; 81; 900? Куб какого числа равен 1; 8; 64; 125; 27 000?
688. Вычислите наиболее простым способом:
а) 4 • 19 • 25; г) 50 • 75 • 2;
б) 8 • 15 • 125; д) 16 • 47 • 125;
в) 250 • 35 • 8; е) 40 • 8 • 25 • 125.
689. Изменится ли частное двух чисел, если:
а) делимое увеличить в 2 раза; в 3 раза;
б) делимое и делитель увеличить в одинаковое число раз?
Приведите примеры.
690. Расскажите, в каком порядке надо выполнять действия при нахождении значения выражения:
а) 23 • 82- 15 • 33+ 1734 : 17;
б) 5 • 113-4 • (76 + 132- 5).
691. Попробуйте найти число, квадрат которого оканчивается цифрой 0; 6; 5; 7.Какой цифрой может оканчиваться квадрат числа? куб числа?
692. Машина двигалась 4 ч со скоростью а км/ч и 3 ч со скоростью b км/ч. Какой путь прошла машина за эти 7 часов?
Составьте выражение для решения задачи и найдите его значение при:
а = 40, b = 30; а = 30, b = 40; а = 60, b = 70.
693. Найдите значение выражения:
а) З2 + 42; в) (92 - 42) : (9 - 4);
б) (42 + 1)2; г) (83 + 73) : (82 - 72).
694. Семье, состоящей из бабушки, папы, мамы, дочери и сына, подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи?
Решение. У первого члена семьи (например, бабушки) есть 5 вариантов выбора, у следующего (пусть это будет папа) остается 4 варианта выбора, следующий (например, мама) будет выбирать уже из 3 чашек, следующий — из двух, последний же получает одну оставшуюся чашку. Покажем эти способы на схеме.
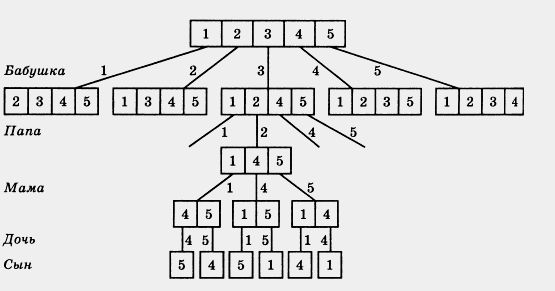
Получили, что каждому выбору чашки бабушкой соответствует четыре возможных выбора папы, т. е. всего 5 • 4 способов. После того как папа выбрал чашку, у мамы есть три варианта выбора, у дочери — два, у сына — один, т. е. всего 3-2-1 способов. Окончательно получаем, что для решения задачи надо найти произведение 5 • 4 • 3 • 2 -1. Заметим, что получили произведение всех натуральных чисел от 1 до 5. Такие произведения записывают короче:
5 • 4 • 3 • 2 • 1 = 5! (читают: «пять факториал»).
Итак, ответ задачи: 5! = 120, т. е. чашки между членами семьи можно распределить ста двадцатью способами.
695. Толя начал читать книгу, когда Сережа прочитал уже 24 страницы такой же книги. Догонит ли Толя Сережу через 5 дней, если будет читать в день — 18 страниц, а Сережа — 12?
696. Начертите координатный луч. Отметьте на нем точки А(5), В(7), С(0) и 0(3). Чему равна длина (в единичных отрезках) отрезков АВ, CD, AD?
697. Через точки Р и К проведите прямую и отметьте на ней точки С и D так, чтобы точка D лежала между Р и /С, а точка Р — между С и D.
698. Докажите, что:
а) 600 < 23 • 35 < 1200;
б) 2400 < 47 • 62 < 3500.
699. Решите задачу:
1) Бронза содержит (по массе) 41 часть меди, 8 частей олова и 1 часть цинка. Какова масса куска бронзы, если в ней олова меньше, чем меди, на 132 г?
2) Дюралюминий — сплав, состоящий из 83 частей алюминия, 5 частей меди, 1 части марганца и 1 части магния (по массе). Какова масса куска дюралюминия, если в нем меди больше, чем магния, на 84 г?
700. Массу М товара с упаковкой (ее называют массой брутто) определяют так: вычисляют массу товара (она называется массой нетто) и прибавляют к ней массу р упаковки. Запишите это правило в виде формулы, если масса одного изделия т и в упаковке n изделий. Найдите по этой формуле массу брутто ящика чая, в котором 50 пачек чая, по 100 г каждая, а масса ящика 1 кг.
701. Найдите по формуле пути:
а) значение s, если v = 12 км/ч, t — 3 ч;
б) значение t, если s = 180 м, v = 15 м/с.
702. Найдите по формуле для нахождения периметра прямоугольника:
а) периметр Р, если а = 15 см, b = 25 см;
б) сторону а, если Р = 122 м, b = 34 м.
703. Периметр квадрата 144 м. Найдите его сторону.
704. Сплав состоит из 19 частей алюминия и 2 частей магния (по массе). Какова масса сплава, если в нем магния на 34 кг меньше, чем алюминия?
705. Митя собрал в 3 раза больше грибов, чем Петя. Подсчитав все собранные грибы, они увидели, что набрали 48 подосиновиков и подберезовиков, а белых грибов — 8. Сколько грибов собрал каждый из мальчиков?
706. Отец старше сына на 20 лет, а сын моложе отца в 5 раз. Сколько лет отцу и сколько лет сыну?
707. Решите уравнение:
а) (Зх + bх) • 18 = 144;
б) (7у - Зу) : 8 = 17;
в) (6а + а) : 13 = 14;
г) 48 : (9b - b) = 2.
708. Выполните действия:
а) 183 340 : 89 • 104;
б) 102 720 : 96 • 203.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Математика для 5 класса, учебники и книги по математике скачать, библиотека онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|