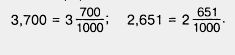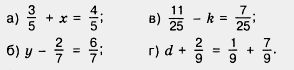|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Сложение, вычитание десятичных дробей</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Сложение, вычитание десятичных дробей, десятичные, дроби, число, координатном луче, отрезка, задачу, вычитание</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Сложение и вычитание десятичных дробей''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Сложение и вычитание десятичных дробей''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' Сложение и вычитание десятичных дробей '''<br> | + | '''Сложение и вычитание десятичных дробей '''<br> |
| | | | |
| - | <br>Сложим десятичные дроби 3,7 и 2,651. Сначала уравняем количество цифр после запятой, приписав к первой дроби два нуля справа: 3,7 = 3,700. Потом <br>запишем числа в смешанной форме: | + | <br>Сложим '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичные]]''' дроби 3,7 и 2,651. Сначала уравняем количество цифр после запятой, приписав к первой дроби два нуля справа: 3,7 = 3,700. Потом запишем числа в смешанной форме: |
| | | | |
| - | [[Image:17-06-130.jpg]]<br><br>Значит, | + | [[Image:17-06-130.jpg|240px|Задание]]<br><br>Значит, |
| | | | |
| - | [[Image:17-06-131.jpg]]<br><br>Тот же ответ можно получить иначе, сложив числа 3,7 и 2,651 «столбиком»: | + | [[Image:17-06-131.jpg|550px|Задание]]<br><br>Тот же ответ можно получить иначе, сложив числа 3,7 и 2,651 «столбиком»: |
| | | | |
| - | [[Image:17-06-132.jpg]]<br> | + | [[Image:17-06-132.jpg|120px|Задание]]<br> |
| | | | |
| - | , <br>I <br>3, <br>700 <br>2. <br>6, <br>69/ <br>35/ <br>Теперь найдем разность тех же чисел: <br>3,7 - 2,651 = 3 <br>700 <br>651 <br>700 - 651 <br>1000 "1000 1000 <br>И здесь ответ можно получить короче: <br>I <br>49 <br>1000 <br>= 1,049. <br>700 <br>2, <br>69/ <br>04? <br>Чтобы сложить (вычесть) десятичные дроби, нужно: <br>1) уравнять в этих дробях количество знаков после запятой] <br>2) записать их друг под другом так, чтобы запятая была записана под за- <br>пятой] <br>3) выполнить сложение (вычитание), не обращая внимания на запятую; <br>4) поставить в ответе запятую под запятой в данных дробях. <br>^ Число 0,444 можно записать в виде суммы: <br>0,444 = 0,400 + 0,040 + 0,004 = 0,4 + 0,04 + 0,004. <br>Оно равно сумме 4 десятых, 4 сотых и 4 тысячных. <br>Таким образом, в записи этого числа первая цифра 4 показывает число <br>десятых, вторая — число сотых, а третья — число тысячных. Поэтому первый <br>разряд после запятой называют разрядом десятых, второй — разрядом со- <br>тых, а третий — разрядом тысячных. <br>Запись 0,444 = 0,4 4- 0,04 + 0,004 называют разложением числа 0,444 <br>по разрядам. <br>В числе 2367,815 высшим (старшим) разрядом являются тысячи, а <br>низшим (младшим) — тысячные. Это число содержит 2 тысячи, 3 сотни, <br>6 десятков, 7 единиц, 8 десятых, 1 сотую и 5 тысячных. <br>Разложение по разрядам позволяет немного по-другому отмечать деся- <br>тичные дроби на координатном луче. <br>Отметим, например, на координатном луче число 1,37. Разложим это <br>число по разрядам: <br>1,37 = 1 + 0,3 + 0,07. <br>191 <br>1 <br>1 1 1 1" <br>1,37 <br>1,3 <br>и—i—i—i—i—h <br>O <br>E <br>Рис. 145 <br>От начала луча отложим 1 единичный отрезок (рис. 145), затем следую- <br>щий единичный отрезок разделим на 10 долей и, отсчитав 3 такие доли <br>(десятые), отметим число 1,3. <br>Потом следующую за числом 1,3 десятую долю единичного отрезка раз- <br>делим еще на 10 долей. Получаем сотые доли единичного отрезка. <br>Отсчитав от числа 1,3 семь сотых долей, получаем число 1,37. <br>Десятичные дроби можно сравнивать и по разрядам. <br>Например, 2,87 < 4,7 потому, что целая часть числа 2,87 меньше целой <br>части числа 4,7 (2 < 4). <br>Сравним числа 2,681 и 2,69. В этих числах целые части и цифры в раз- <br>ряде десятых одинаковы, но число в разряде сотых меньше у первой <br>десятичной дроби, чем у второй (8 < 9). Поэтому 2,681 < 2,69. <br>Как складывают и как вычитают десятичные дроби? <br>Назовите первые три разряда после запятой в десятичных дробях. <br># Как сравнивают десятичные дроби по разрядам? <br>* Что показывает в десятичной дроби первая цифра после запятой? <br>А вторая цифра? <br>1211. На пальто израсходовали 3,2 м ткани, а на костюм — 2,63 м. <br>Сколько ткани израсходовали на пальто и костюм вместе? Решите задачу <br>сложением десятичных дробей и путем перехода к сантиметрам. <br>1212. Масса автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» <br>14,2 ц. На сколько масса «Волги» больше массы «Нивы»? Решите задачу <br>с помощью десятичных дробей и переводом данных в килограммы. <br>1213. Выполните сложение: <br>а) 0,769 + 42,389; г) 8,9021 + 0,68; <br>б) 5,8 + 22,191; д) 2,7 + 1,35 + 0,8; <br>в) 95,381 + 3,219; е) 13,75 + 8,2 + 0,115. <br>1214. Выполните вычитание: <br>а) 9,4 - 7,3; г) 11,1 - 2,8; <br>б) 16,78 - 5,48; д) 88,252 - 4,69; <br>в) 7,79 - 3,79; е) 6,6 - 5,99. <br>22, <br>191 <br>>, <br>88. <br>252 <br>У,о9 <br>192 <br>1215. С одного участка собрали 95,37 т зерна, а с другого — на 16,8 т <br>больше. Сколько тонн зерна собрали с двух участков? <br>1216. Один тракторист вспахал 13,8 га земли, что оказалось на 4,7 га <br>меньше, чем вспахал второй тракторист. Сколько гектаров земли вспахали <br>оба тракториста вместе? <br>1217. От куска провода длиной 30 м отрезали 4,75 м. Сколько метров <br>провода осталось в куске? <br>1218. Груз, поднимаемый вертолетом, легче вертолета на 4,72 т. Какова <br>масса вертолета вместе с грузом, если масса груза 1,24 т? <br>1219. Выполните действие: <br>а) 7,8 + 6,9; д) 24,2 + 0,867; и) 1 - 0,999; <br>б) 129 + 9,72; е) 830 - 0,0097; к) 425 - 2,647; <br>в) 8,1 - 5,46; ж) 0,02 - 0,0156; л) 83 - 82,877; <br>г) 96,3 - 0,081; з) 0,003 - 0,00089; м) 37,2 - 0,03. <br>1220. Собственная скорость катера (скорость в стоячей воде) равна <br>21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по <br>течению и против течения. <br>1221. Скорость теплохода по течению равна 37,6 км/ч. Найдите соб- <br>ственную скорость теплохода и его скорость против течения, если скорость <br>течения реки 3,9 км/ч. <br>1222. Скорость велосипедиста 15 км/ч, а скорость пешехода на 9,7 км/ч <br>меньше. На сколько уменьшится расстояние между ними за 1 ч, если они <br>движутся навстречу друг другу? На сколько увеличивается расстояние <br>между ними за 1 ч, если они движутся из одной точки в противополож- <br>ные стороны? <br>1223. Расстояние между городами 156 км. Из них навстречу друг другу <br>выехали два велосипедиста. Один проезжает в час 13,6 км, а второй — <br>10,4 км. Через сколько часов они встретятся? <br>1224. Веревку разрезали на пять кусков. Первый кусок больше второго <br>на 4,2 м, но меньше третьего на 2,3 м. Четвертый кусок больше пятого <br>на 3,7 м, но меньше третьего на 1,3 м. Какова длина веревки, если длина <br>четвертого куска 7,8 м? <br>1225. Найдите периметр треугольника ABC, если АВ = 2,8 см, ВС боль- <br>ше АВ на 0,8 см, но меньше АС на 1,1 см. <br>1226. Используя буквы х и у> запишите переместительное свойство сло- <br>жения и проверьте его, если х = 7,3, а у = 29. <br>Используя буквы a, b и с, запишите сочетательное свойство сложения <br>и проверьте его при а = 2,3; Ъ = 4,2 и с = 3,7. <br>Л 93 <br>7 Математика 5 кл <br>1227. Используя буквы а, Ь и с, запишите свойство вычитания числа <br>из суммы и свойство вычитания суммы из числа. Проверьте эти свойства <br>при а = 13,2; Ь = 4,8 и с = 2,7. <br>1228. Используя свойства сложения и вычитания, вычислите самым <br>удобным способом значение выражения: <br>а) 2,31 + (7,65 + 8,69); <br>б) 0,387 + (0,613 + 3,142); <br>в) (7,891 + 3,9) + (6,1 + 2,109); <br>г) 14,537 - (2,237 + 5,9); <br>д) (24,302 + 17,879) - 1,302; <br>е) (25,243 + 17,77) - 2,77. <br>1229. Выполните действия: <br>а) 9,83 - 1,76 - 3,28 + 0,11; в) 14,87 - (5,82 - 3,27); <br>б) 12,371 - 8,93 + 1,212; г) 14 - (3,96 + 7,85). <br>1230. Сколько единиц в каждом разряде числа: 32,547; 2,6034? <br>1231. Разложите по разрядам число: <br>а) 24,578; б) 0,520001. <br>1232. Запишите десятичную дробь, в которой: <br>а) 15 целых, 3 десятых, 7 сотых и 9 тысячных; <br>б) 0 целых, 3 десятых, 0 сотых и 4 тысячных. <br>1233. Выразите длину отрезка АВ = 5 м 7 дм 6 см 2 мм: <br>а) в метрах; в) в сантиметрах; <br>б) в дециметрах; г) в миллиметрах. <br>Выразите длину отрезка СМ в метрах, дециметрах, сантиметрах и мил- <br>лиметрах, если СМ = 4,573 м. <br>1234. Отметьте на координатном луче точки с координатами: 0,46; 0,8; <br>1,25; 0,36; 0,77; 1,47. Единичный отрезок равен 1 дм. <br>1235. Найдите координаты точек А, Б, С, D и К (рис. 146). <br>5 6 <br>—I—I—I—I—|—I—I—I—I—|—I—I—I—|—I—I—I—|—I—|—I—I— <br>А В С D К <br>Рис. 146 <br>1236. Зная, что 11,87 - 7,39 = 4,48, найдите значение выражения или <br>решите уравнение: <br>а) 7,39 + 4,48; г) 7,39 + у = 11,87; <br>б) 11,87 - 4,48; д) 4,48 + z = 11,87; <br>в) х- 7,39 = 4,48; е) 11,87 - р = 7,39. <br>194 <br>1237. Прочитайте показания термомет- <br>ров (рис. 147). Сколько градусов будет по- <br>казывать каждый из них, если его столбик: <br>а) поднимется на 4 малых деле- <br>ния; на 2 больших деления; <br>на 0,5°С; на 1,3°С; <br>б) опустится на 7 малых делений; <br>на одно большое деление; на <br>0,3°С; на 1,4°С? <br>1238. Решите уравнение: <br>а) г Л- 3,8 = 8; <br>б) у - 6,5 « 12; <br>в) 13,5 - х = 1,8; <br>г)Л5,4 + k = 15,4; <br>д) 2,8 + I + 3,7 = 12,5; <br>е) (5,6 - г) + 3,8 = 4,4. <br>1239. Вычислите устно: <br>а) 60 - 36 <br>• 3 <br>: 4 <br>+ 27 <br>: 3 <br>б) 55 + 25 <br>: 5 <br>+ 7 <br>• 3 <br>+ 31 <br>в) 75 : 25 <br>• 15 <br>: 9 <br>• 12 <br>+ 240 <br>г) 15-6 <br>- 39 <br>: 17 <br>• 18 <br>+ 46 <br>Д) 45 <br>+ 30 <br>: 15 <br>• 20 <br>-34 <br>: 11 <br>Рис. 147 <br>1240. Восстановите цепочку вычислений <br>J <br>> <br>+ 2 <br>i^- <br>Ш: <br>195 <br>1241. Назовите какое-либо число, расположенное на координатном луче: <br>а) между числами 0,1 и 0,2; <br>б) между 0,02 и 0,03; <br>в) левее 0,001, но правее 0. <br>1242. Какую часть квадратного метра составляет: <br>а) 1 дм2; б) 1 см2; в) 10 дм2; г) 100 см2? <br>3 4 5 <br>1243. Стороны треугольника j м — м - м. Найдите его периметр. <br>3 <br>1244. Найдите число, если т^ его равны: 30; 15; 6. <br>1245. Какая часть периода хоккейного матча сыграна, если с начала мат- <br>ча прошло: 5 мин; 10 мин; 15 мин; 1 мин 20 с; 20 с? (Период продолжается <br>20 мин.) <br>1246. Сколько Буратино заплатил за арбуз, который стоил 20 сольдо и <br>еще пол-арбуза? <br>1247. Сравните числа: <br>а) 12,567 и 125,67; б) 7,399 и 7,4. <br>1248. Между какими двумя соседними натуральными числами находится <br>число: <br>а) 5,1; 6)6,32; в) 9,999; г) 25,257? <br>1249. Расставьте в порядке убывания числа: 0,915; 2,314; 0,9078; 2,316; <br>2,31; 10,45. <br>1250. Расставьте в порядке возрастания величины: 8,09 км; 8165,3 м; <br>8 154 257 мм; 815 376 см. <br>1251. Решите уравнение: <br>а) <br>б) <br>3 <br>5 Н <br>у- <br>У X = <br>2 <br>7 <br>4. <br>5' <br>6. <br>7' <br>В) <br>г) <br>11 <br>25 <br>d + <br>— <br>2 <br>9 <br>k = <br>= <br>7 . <br>25' <br>1 <br>9 <br>7 <br>9 <br>1252. Выразите: <br>а) в метрах: 17 м 8 см; 8 м 17 см; 4 см; 15 дм; <br>б) в тоннах: 3 т 8 ц 67 кг; 1244 кг; 710 кг. <br>1253. Решите задачу: <br>1) На машину погрузили 7 одинаковых мешков с мукой и 12 одинаковых <br>мешков с крупой. Масса мешка с мукой в 2 раза больше массы мешка с кру- <br>пой. Найдите массу мешка с мукой и мешка с крупой, если всего на машину <br>погрузили 780 кг. <br>2) Масса индюка меньше массы овцы в 3 раза, а масса трех таких овец <br>больше массы пяти индюков на 60 кг. Какова масса одного индюка и какова <br>масса одной овцы? <br>1254. Разгадайте чайнворд, помещенный на форзаце в конце учебника. <br>196 <br>1255. Выполните сложение: <br>а) 395,486 + 4,58; г) 1,9679 + 269,0121; <br>б) 7,6 + 908,67; д) 23,84 + 0,267; <br>в) 0,54 + 24,1789; е) 0,01237 + 0,0009876. <br>1256. Выполните вычитание: <br>а) 0,59 - 0,27; г) 18,01 - 2,9; ж) 7,45 - 4,45; <br>б) 6,05 - 2,87; д) 15 - 1,12; з) 206,48 - 90,507; <br>в) 3,1 - 0,09; е) 3 - 0,07; и) 0,067 - 0,00389. <br>1257. Одна из сторон треугольника 83,6 см, вторая на 14,8 см длиннее <br>первой, а третья на 8,6 см длиннее второй. Найдите периметр треуголь- <br>ника. <br>1258. Трубу длиной 9,35 м разрезали на две части. Длина одной части <br>2,89 м. На сколько метров вторая часть длиннее первой? <br>1259. Воздушный шар состоит из оболочки, гондолы для пассажиров <br>и газовой горелки для нагрева воздуха внутри оболочки. Масса гондолы <br>0,24 т, и она меньше массы оболочки на 0,32 т, но больше массы газовой <br>горелки на 0,15 т. Какова масса воздушного шара? <br>1260. Автомашина в первый час прошла 48,3 км, во второй час — <br>на 15,8 км меньше, чем в первый, а в третий час — на 24,3 км меньше, <br>чем за первые два часа вместе. Какой путь прошла автомашина за эти три <br>часа? <br>1261. Собственная скорость теплохода 40,5 км/ч, а скорость течения <br>5,8 км/ч. Найдите скорость теплохода по течению и против течения. <br>1262. Скорость катера по течению 23,7 км/ч. Найдите собственную <br>скорость катера и его скорость против течения, если скорость течения <br>3,8 км/ч. <br>1263. Выполните действия: <br>а) 73,12 - (5,34 + 13,12); <br>б) 101,3 + (84,7 + 1,11); <br>в) (47,28 - 34,98) + (55,02 + 34,98); <br>г) (46,83 + 15,77) - (6,83 - 5,77). <br>1264. Разложите по разрядам числа: 41,87; 0,6098; 13,5401. <br>1265. Запишите десятичную дробь, в которой: <br>а) 21 целая, 2 десятых, 8 сотых; <br>б) 0 целых, 0 десятых, 3 сотых, 5 тысячных. <br>1266. Выразите длину отрезка АВ в метрах, дециметрах, сантиметрах <br>и миллиметрах, если АВ = 8,906 м. <br>1267. Отметьте на координатном луче числа: 0,25; 0,5; 0,9; 0,37; 0,73; <br>1,24. За единичный отрезок примите 1 дм. <br>197 <br>1268. Решите уравнение: <br>а) (х - 18,2) + 3,8 = 15,6; в) 16,5 - (t + 3,4) = 4,9; <br>б) 34,2 - (17,9 - у) = 22; г) г + 16,23 - 15,8 = 7,1. <br>1269. Объем прямоугольного параллелепипеда 84 см3. Этот параллеле- <br>пипед разделили на две части. Найдите объем каждой части, если: <br>а) объем одной части в 6 раз больше объема другой; <br>б) объем одной части на 40 см3 больше объема другой. <br><br>
| + | <br>Теперь найдем разность тех же чисел: <br> |
| | + | |
| | + | [[Image:17-06-133.jpg|480px|Задание]]<br><br>И здесь ответ можно получить короче: <br> |
| | + | |
| | + | [[Image:17-06-134.jpg|120px|Задание]]<br><br>Чтобы сложить (вычесть) десятичные '''[[Фішки для допитливих до уроку: Дробові числа. Звичайні дроби.|дроби]]''', нужно: <br> |
| | + | |
| | + | 1) уравнять в этих дробях количество знаков после запятой<br>2) записать их друг под другом так, чтобы запятая была записана под запятой<br>3) выполнить сложение (вычитание), не обращая внимания на запятую; <br>4) поставить в ответе запятую под запятой в данных дробях. <br> |
| | + | |
| | + | Число 0,444 можно записать в виде суммы: <br> |
| | + | |
| | + | 0,444 = 0,400 + 0,040 + 0,004 = 0,4 + 0,04 + 0,004. <br> |
| | + | |
| | + | Оно равно сумме 4 десятых, 4 сотых и 4 тысячных. |
| | + | |
| | + | Таким образом, в записи этого числа первая цифра 4 показывает '''[[Додавання і віднімання натуральних чисел|число]]''' десятых, вторая — число сотых, а третья — число тысячных. Поэтому первый разряд после запятой называют разрядом десятых, второй — разрядом сотых, а третий — разрядом тысячных. <br> |
| | + | |
| | + | Запись 0,444 = 0,4 4- 0,04 + 0,004 называют разложением числа 0,444 по разрядам. <br> |
| | + | |
| | + | В числе 2367,815 высшим (старшим) разрядом являются тысячи, а низшим (младшим) — тысячные. Это число содержит 2 тысячи, 3 сотни, 6 десятков, 7 единиц, 8 десятых, 1 сотую и 5 тысячных. <br> |
| | + | |
| | + | Разложение по разрядам позволяет немного по-другому отмечать десятичные дроби на '''[[Порівняння натуральних чисел за допомогою координатного променя. Презентація уроку|координатном луче]]'''. <br>Отметим, например, на координатном луче число 1,37. Разложим это число по разрядам: |
| | + | |
| | + | 1,37 = 1 + 0,3 + 0,07. <br> |
| | + | |
| | + | [[Image:17-06-135.jpg|480px|Задание]] |
| | + | |
| | + | <br>От начала луча отложим 1 единичный отрезок (рис. 145), затем следующий единичный отрезок разделим на 10 долей и, отсчитав 3 такие доли (десятые), отметим число 1,3. |
| | + | |
| | + | Потом следующую за числом 1,3 десятую долю единичного '''[[Отрезок. Длина отрезка. Треугольник|отрезка]]''' разделим еще на 10 долей. Получаем сотые доли единичного отрезка. |
| | + | |
| | + | Отсчитав от числа 1,3 семь сотых долей, получаем число 1,37. |
| | + | |
| | + | Десятичные дроби можно сравнивать и по разрядам. |
| | + | |
| | + | Например, 2,87 < 4,7 потому, что целая часть числа 2,87 меньше целой части числа 4,7 (2 < 4). |
| | + | |
| | + | Сравним числа 2,681 и 2,69. В этих числах целые части и цифры в разряде десятых одинаковы, но число в разряде сотых меньше у первой десятичной дроби, чем у второй (8 < 9). Поэтому 2,681 < 2,69. |
| | + | |
| | + | <br>''Как складывают и как вычитают десятичные дроби? <br>Назовите первые три разряда после запятой в десятичных дробях. <br>Как сравнивают десятичные дроби по разрядам? <br>Что показывает в десятичной дроби первая цифра после запятой? <br>А вторая цифра? '' |
| | + | |
| | + | <br>1211. На пальто израсходовали 3,2 м ткани, а на костюм — 2,63 м. Сколько ткани израсходовали на пальто и костюм вместе? Решите '''[[Ознайомлення з поняттям і терміном „задача”. Складання і розв’язування задачі на знаходження суми і остачі. Презентація уроку|задачу]]''' сложением десятичных дробей и путем перехода к сантиметрам. |
| | + | |
| | + | 1212. Масса автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» 14,2 ц. На сколько масса «Волги» больше массы «Нивы»? Решите задачу с помощью десятичных дробей и переводом данных в килограммы. |
| | + | |
| | + | 1213. Выполните сложение: |
| | + | |
| | + | а) 0,769 + 42,389; г) 8,9021 + 0,68; <br>б) 5,8 + 22,191; д) 2,7 + 1,35 + 0,8; <br>в) 95,381 + 3,219; е) 13,75 + 8,2 + 0,115. |
| | + | |
| | + | 1214. Выполните вычитание: |
| | + | |
| | + | а) 9,4 - 7,3; г) 11,1 - 2,8; <br>б) 16,78 - 5,48; д) 88,252 - 4,69; <br>в) 7,79 - 3,79; е) 6,6 - 5,99. <br> |
| | + | |
| | + | [[Image:17-06-136.jpg|120px|Задание]] |
| | + | |
| | + | <br>1215. С одного участка собрали 95,37 т зерна, а с другого — на 16,8 т больше. Сколько тонн зерна собрали с двух участков? |
| | + | |
| | + | 1216. Один тракторист вспахал 13,8 га земли, что оказалось на 4,7 га меньше, чем вспахал второй тракторист. Сколько гектаров земли вспахали оба тракториста вместе? |
| | + | |
| | + | 1217. От куска провода длиной 30 м отрезали 4,75 м. Сколько метров провода осталось в куске? |
| | + | |
| | + | 1218. Груз, поднимаемый вертолетом, легче вертолета на 4,72 т. Какова масса вертолета вместе с грузом, если масса груза 1,24 т? |
| | + | |
| | + | 1219. Выполните действие: |
| | + | |
| | + | а) 7,8 + 6,9; д) 24,2 + 0,867; и) 1 - 0,999; <br>б) 129 + 9,72; е) 830 - 0,0097; к) 425 - 2,647; <br>в) 8,1 - 5,46; ж) 0,02 - 0,0156; л) 83 - 82,877; <br>г) 96,3 - 0,081; з) 0,003 - 0,00089; м) 37,2 - 0,03. |
| | + | |
| | + | 1220. Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения. |
| | + | |
| | + | 1221. Скорость теплохода по течению равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч. |
| | + | |
| | + | 1222. Скорость велосипедиста 15 км/ч, а скорость пешехода на 9,7 км/ч меньше. На сколько уменьшится расстояние между ними за 1 ч, если они движутся навстречу друг другу? На сколько увеличивается расстояние между ними за 1 ч, если они движутся из одной точки в противоположные стороны? |
| | + | |
| | + | 1223. Расстояние между городами 156 км. Из них навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а второй — 10,4 км. Через сколько часов они встретятся? |
| | + | |
| | + | 1224. Веревку разрезали на пять кусков. Первый кусок больше второго на 4,2 м, но меньше третьего на 2,3 м. Четвертый кусок больше пятого на 3,7 м, но меньше третьего на 1,3 м. Какова длина веревки, если длина четвертого куска 7,8 м? |
| | + | |
| | + | 1225. Найдите периметр треугольника ABC, если АВ = 2,8 см, ВС больше АВ на 0,8 см, но меньше АС на 1,1 см. |
| | + | |
| | + | 1226. Используя буквы х и у> запишите переместительное свойство сложения и проверьте его, если х = 7,3, а у = 29. <br>Используя буквы a, b и с, запишите сочетательное свойство сложения и проверьте его при а = 2,3; b = 4,2 и с = 3,7. |
| | + | |
| | + | 1227. Используя буквы а, Ь и с, запишите свойство вычитания числа из суммы и свойство вычитания суммы из числа. Проверьте эти свойствапри а = 13,2; b = 4,8 и с = 2,7. |
| | + | |
| | + | 1228. Используя свойства сложения и вычитания, вычислите самым удобным способом значение выражения: |
| | + | |
| | + | а) 2,31 + (7,65 + 8,69); <br>б) 0,387 + (0,613 + 3,142); <br>в) (7,891 + 3,9) + (6,1 + 2,109); <br>г) 14,537 - (2,237 + 5,9); <br>д) (24,302 + 17,879) - 1,302; <br>е) (25,243 + 17,77) - 2,77. |
| | + | |
| | + | 1229. Выполните действия: |
| | + | |
| | + | а) 9,83 - 1,76 - 3,28 + 0,11; в) 14,87 - (5,82 - 3,27); <br>б) 12,371 - 8,93 + 1,212; г) 14 - (3,96 + 7,85). |
| | + | |
| | + | 1230. Сколько единиц в каждом разряде числа: 32,547; 2,6034? |
| | + | |
| | + | 1231. Разложите по разрядам число: |
| | + | |
| | + | а) 24,578; |
| | + | |
| | + | б) 0,520001. |
| | + | |
| | + | 1232. Запишите десятичную дробь, в которой: |
| | + | |
| | + | а) 15 целых, 3 десятых, 7 сотых и 9 тысячных; <br>б) 0 целых, 3 десятых, 0 сотых и 4 тысячных. |
| | + | |
| | + | 1233. Выразите длину отрезка АВ = 5 м 7 дм 6 см 2 мм: |
| | + | |
| | + | а) в метрах; в) в сантиметрах; <br>б) в дециметрах; г) в миллиметрах. |
| | + | |
| | + | Выразите длину отрезка СМ в метрах, дециметрах, сантиметрах и миллиметрах, если СМ = 4,573 м. |
| | + | |
| | + | 1234. Отметьте на координатном луче точки с координатами: 0,46; 0,8; 1,25; 0,36; 0,77; 1,47. Единичный отрезок равен 1 дм. |
| | + | |
| | + | 1235. Найдите координаты точек А, B, С, D и К (рис. 146). |
| | + | |
| | + | [[Image:17-06-137.jpg|480px|Задание]]<br><br>1236. Зная, что 11,87 - 7,39 = 4,48, найдите значение выражения или решите уравнение: |
| | + | |
| | + | а) 7,39 + 4,48; г) 7,39 + у = 11,87; <br>б) 11,87 - 4,48; д) 4,48 + z = 11,87; <br>в) х- 7,39 = 4,48; е) 11,87 - р = 7,39. <br><br>1237. Прочитайте показания термометров (рис. 147). Сколько градусов будет показывать каждый из них, если его столбик: |
| | + | |
| | + | а) поднимется на 4 малых деления; на 2 больших деления; на 0,5°С; на 1,3°С; <br>б) опустится на 7 малых делений; на одно большое деление; на 0,3°С; на 1,4°С? |
| | + | |
| | + | [[Image:17-06-138.jpg|240px|Термометр]] |
| | + | |
| | + | <br>1238. Решите уравнение: |
| | + | |
| | + | а)z + 3,8 = 8; <br>б) у - 6,5 = 12; <br>в) 13,5 - х = 1,8; <br>г)15,4 + k = 15,4; <br>д) 2,8 + I + 3,7 = 12,5; <br>е) (5,6 - г) + 3,8 = 4,4. |
| | + | |
| | + | 1239. Вычислите устно: |
| | + | |
| | + | [[Image:17-06-139.jpg|320px|Задание]]<br><br>1240. Восстановите цепочку вычислений |
| | + | |
| | + | [[Image:17-06-140.jpg|550px|Задание]]<br><br>1241. Назовите какое-либо число, расположенное на координатном луче: |
| | + | |
| | + | а) между числами 0,1 и 0,2; <br>б) между 0,02 и 0,03; <br>в) левее 0,001, но правее 0. |
| | + | |
| | + | 1242. Какую часть квадратного метра составляет: |
| | + | |
| | + | а) 1 дм2; б) 1 см2; в) 10 дм2; г) 100 см2? |
| | + | |
| | + | 1243. Стороны треугольника [[Image:17-06-141.jpg]]. Найдите его периметр. <br>1244. Найдите число, если [[Image:17-06-142.jpg]] его равны: 30; 15; 6. <br>1245. Какая часть периода хоккейного матча сыграна, если с начала матча прошло: 5 мин; 10 мин; 15 мин; 1 мин 20 с; 20 с? (Период продолжается 20 мин.) |
| | + | |
| | + | 1246. Сколько Буратино заплатил за арбуз, который стоил 20 сольдо и еще пол-арбуза? |
| | + | |
| | + | 1247. Сравните числа: |
| | + | |
| | + | а) 12,567 и 125,67; |
| | + | |
| | + | б) 7,399 и 7,4. |
| | + | |
| | + | 1248. Между какими двумя соседними натуральными числами находится число: |
| | + | |
| | + | а) 5,1; б)6,32; в) 9,999; г) 25,257? |
| | + | |
| | + | 1249. Расставьте в порядке убывания числа: 0,915; 2,314; 0,9078; 2,316; 2,31; 10,45. |
| | + | |
| | + | 1250. Расставьте в порядке возрастания величины: 8,09 км; 8165,3 м; 8 154 257 мм; 815 376 см. |
| | + | |
| | + | 1251. Решите уравнение: |
| | + | |
| | + | [[Image:17-06-143.jpg|320px|Задание]]<br><br>1252. Выразите: |
| | + | |
| | + | а) в метрах: 17 м 8 см; 8 м 17 см; 4 см; 15 дм; <br>б) в тоннах: 3 т 8 ц 67 кг; 1244 кг; 710 кг. |
| | + | |
| | + | 1253. Решите задачу: |
| | + | |
| | + | 1) На машину погрузили 7 одинаковых мешков с мукой и 12 одинаковых мешков с крупой. Масса мешка с мукой в 2 раза больше массы мешка с крупой. Найдите массу мешка с мукой и мешка с крупой, если всего на машину погрузили 780 кг. |
| | + | |
| | + | 2) Масса индюка меньше массы овцы в 3 раза, а масса трех таких овец больше массы пяти индюков на 60 кг. Какова масса одного индюка и какова масса одной овцы? |
| | + | |
| | + | 1254. Разгадайте чайнворд, помещенный на форзаце в конце [http://xvatit.com/vuzi/ '''учебника''']. |
| | + | |
| | + | 1255. Выполните сложение: |
| | + | |
| | + | а) 395,486 + 4,58; г) 1,9679 + 269,0121; <br>б) 7,6 + 908,67; д) 23,84 + 0,267; <br>в) 0,54 + 24,1789; е) 0,01237 + 0,0009876. |
| | + | |
| | + | 1256. Выполните '''[[Сложение и вычитание одночленов|вычитание]]''': |
| | + | |
| | + | а) 0,59 - 0,27; г) 18,01 - 2,9; ж) 7,45 - 4,45; <br>б) 6,05 - 2,87; д) 15 - 1,12; з) 206,48 - 90,507; <br>в) 3,1 - 0,09; е) 3 - 0,07; и) 0,067 - 0,00389. |
| | + | |
| | + | 1257. Одна из сторон треугольника 83,6 см, вторая на 14,8 см длиннее первой, а третья на 8,6 см длиннее второй. Найдите периметр треугольника. |
| | + | |
| | + | 1258. Трубу длиной 9,35 м разрезали на две части. Длина одной части 2,89 м. На сколько метров вторая часть длиннее первой? |
| | + | |
| | + | 1259. Воздушный шар состоит из оболочки, гондолы для пассажиров и газовой горелки для нагрева воздуха внутри оболочки. Масса гондолы 0,24 т, и она меньше массы оболочки на 0,32 т, но больше массы газовой горелки на 0,15 т. Какова масса воздушного шара? |
| | + | |
| | + | 1260. Автомашина в первый час прошла 48,3 км, во второй час — на 15,8 км меньше, чем в первый, а в третий час — на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа? |
| | + | |
| | + | 1261. Собственная скорость теплохода 40,5 км/ч, а скорость течения 5,8 км/ч. Найдите скорость теплохода по течению и против течения. |
| | + | |
| | + | 1262. Скорость катера по течению 23,7 км/ч. Найдите собственную скорость катера и его скорость против течения, если скорость течения 3,8 км/ч. |
| | + | |
| | + | 1263. Выполните действия: |
| | + | |
| | + | а) 73,12 - (5,34 + 13,12); <br>б) 101,3 + (84,7 + 1,11); <br>в) (47,28 - 34,98) + (55,02 + 34,98); <br>г) (46,83 + 15,77) - (6,83 - 5,77). |
| | + | |
| | + | 1264. Разложите по разрядам числа: |
| | + | |
| | + | 41,87; 0,6098; 13,5401. |
| | + | |
| | + | 1265. Запишите десятичную дробь, в которой: |
| | + | |
| | + | а) 21 целая, 2 десятых, 8 сотых; <br>б) 0 целых, 0 десятых, 3 сотых, 5 тысячных. |
| | + | |
| | + | 1266. Выразите длину отрезка АВ в метрах, дециметрах, сантиметрах и миллиметрах, если АВ = 8,906 м. |
| | + | |
| | + | 1267. Отметьте на координатном луче числа: 0,25; 0,5; 0,9; 0,37; 0,73; 1,24. За единичный отрезок примите 1 дм. |
| | + | |
| | + | 1268. Решите уравнение: |
| | + | |
| | + | а) (х - 18,2) + 3,8 = 15,6; в) 16,5 - (t + 3,4) = 4,9; <br>б) 34,2 - (17,9 - у) = 22; г) г + 16,23 - 15,8 = 7,1. |
| | + | |
| | + | 1269. Объем прямоугольного параллелепипеда 84 см<sup>3</sup>. Этот параллелепипед разделили на две части. Найдите объем каждой части, если: |
| | + | |
| | + | а) объем одной части в 6 раз больше объема другой; <br>б) объем одной части на 40 см<sup>3</sup> больше объема другой. |
| | | | |
| | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub>
| |
| | | | |
| - | <br> | + | |
| | + | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub><br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:44, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей
Сложим десятичные дроби 3,7 и 2,651. Сначала уравняем количество цифр после запятой, приписав к первой дроби два нуля справа: 3,7 = 3,700. Потом запишем числа в смешанной форме:
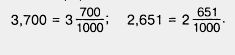
Значит,
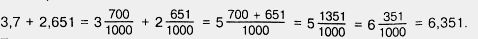
Тот же ответ можно получить иначе, сложив числа 3,7 и 2,651 «столбиком»:

Теперь найдем разность тех же чисел:
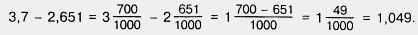
И здесь ответ можно получить короче:

Чтобы сложить (вычесть) десятичные дроби, нужно:
1) уравнять в этих дробях количество знаков после запятой
2) записать их друг под другом так, чтобы запятая была записана под запятой
3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) поставить в ответе запятую под запятой в данных дробях.
Число 0,444 можно записать в виде суммы:
0,444 = 0,400 + 0,040 + 0,004 = 0,4 + 0,04 + 0,004.
Оно равно сумме 4 десятых, 4 сотых и 4 тысячных.
Таким образом, в записи этого числа первая цифра 4 показывает число десятых, вторая — число сотых, а третья — число тысячных. Поэтому первый разряд после запятой называют разрядом десятых, второй — разрядом сотых, а третий — разрядом тысячных.
Запись 0,444 = 0,4 4- 0,04 + 0,004 называют разложением числа 0,444 по разрядам.
В числе 2367,815 высшим (старшим) разрядом являются тысячи, а низшим (младшим) — тысячные. Это число содержит 2 тысячи, 3 сотни, 6 десятков, 7 единиц, 8 десятых, 1 сотую и 5 тысячных.
Разложение по разрядам позволяет немного по-другому отмечать десятичные дроби на координатном луче.
Отметим, например, на координатном луче число 1,37. Разложим это число по разрядам:
1,37 = 1 + 0,3 + 0,07.
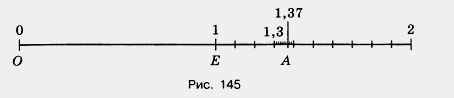
От начала луча отложим 1 единичный отрезок (рис. 145), затем следующий единичный отрезок разделим на 10 долей и, отсчитав 3 такие доли (десятые), отметим число 1,3.
Потом следующую за числом 1,3 десятую долю единичного отрезка разделим еще на 10 долей. Получаем сотые доли единичного отрезка.
Отсчитав от числа 1,3 семь сотых долей, получаем число 1,37.
Десятичные дроби можно сравнивать и по разрядам.
Например, 2,87 < 4,7 потому, что целая часть числа 2,87 меньше целой части числа 4,7 (2 < 4).
Сравним числа 2,681 и 2,69. В этих числах целые части и цифры в разряде десятых одинаковы, но число в разряде сотых меньше у первой десятичной дроби, чем у второй (8 < 9). Поэтому 2,681 < 2,69.
Как складывают и как вычитают десятичные дроби?
Назовите первые три разряда после запятой в десятичных дробях.
Как сравнивают десятичные дроби по разрядам?
Что показывает в десятичной дроби первая цифра после запятой?
А вторая цифра?
1211. На пальто израсходовали 3,2 м ткани, а на костюм — 2,63 м. Сколько ткани израсходовали на пальто и костюм вместе? Решите задачу сложением десятичных дробей и путем перехода к сантиметрам.
1212. Масса автомобиля «Нива» 11,5 ц, а масса автомобиля «Волга» 14,2 ц. На сколько масса «Волги» больше массы «Нивы»? Решите задачу с помощью десятичных дробей и переводом данных в килограммы.
1213. Выполните сложение:
а) 0,769 + 42,389; г) 8,9021 + 0,68;
б) 5,8 + 22,191; д) 2,7 + 1,35 + 0,8;
в) 95,381 + 3,219; е) 13,75 + 8,2 + 0,115.
1214. Выполните вычитание:
а) 9,4 - 7,3; г) 11,1 - 2,8;
б) 16,78 - 5,48; д) 88,252 - 4,69;
в) 7,79 - 3,79; е) 6,6 - 5,99.

1215. С одного участка собрали 95,37 т зерна, а с другого — на 16,8 т больше. Сколько тонн зерна собрали с двух участков?
1216. Один тракторист вспахал 13,8 га земли, что оказалось на 4,7 га меньше, чем вспахал второй тракторист. Сколько гектаров земли вспахали оба тракториста вместе?
1217. От куска провода длиной 30 м отрезали 4,75 м. Сколько метров провода осталось в куске?
1218. Груз, поднимаемый вертолетом, легче вертолета на 4,72 т. Какова масса вертолета вместе с грузом, если масса груза 1,24 т?
1219. Выполните действие:
а) 7,8 + 6,9; д) 24,2 + 0,867; и) 1 - 0,999;
б) 129 + 9,72; е) 830 - 0,0097; к) 425 - 2,647;
в) 8,1 - 5,46; ж) 0,02 - 0,0156; л) 83 - 82,877;
г) 96,3 - 0,081; з) 0,003 - 0,00089; м) 37,2 - 0,03.
1220. Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения.
1221. Скорость теплохода по течению равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч.
1222. Скорость велосипедиста 15 км/ч, а скорость пешехода на 9,7 км/ч меньше. На сколько уменьшится расстояние между ними за 1 ч, если они движутся навстречу друг другу? На сколько увеличивается расстояние между ними за 1 ч, если они движутся из одной точки в противоположные стороны?
1223. Расстояние между городами 156 км. Из них навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а второй — 10,4 км. Через сколько часов они встретятся?
1224. Веревку разрезали на пять кусков. Первый кусок больше второго на 4,2 м, но меньше третьего на 2,3 м. Четвертый кусок больше пятого на 3,7 м, но меньше третьего на 1,3 м. Какова длина веревки, если длина четвертого куска 7,8 м?
1225. Найдите периметр треугольника ABC, если АВ = 2,8 см, ВС больше АВ на 0,8 см, но меньше АС на 1,1 см.
1226. Используя буквы х и у> запишите переместительное свойство сложения и проверьте его, если х = 7,3, а у = 29.
Используя буквы a, b и с, запишите сочетательное свойство сложения и проверьте его при а = 2,3; b = 4,2 и с = 3,7.
1227. Используя буквы а, Ь и с, запишите свойство вычитания числа из суммы и свойство вычитания суммы из числа. Проверьте эти свойствапри а = 13,2; b = 4,8 и с = 2,7.
1228. Используя свойства сложения и вычитания, вычислите самым удобным способом значение выражения:
а) 2,31 + (7,65 + 8,69);
б) 0,387 + (0,613 + 3,142);
в) (7,891 + 3,9) + (6,1 + 2,109);
г) 14,537 - (2,237 + 5,9);
д) (24,302 + 17,879) - 1,302;
е) (25,243 + 17,77) - 2,77.
1229. Выполните действия:
а) 9,83 - 1,76 - 3,28 + 0,11; в) 14,87 - (5,82 - 3,27);
б) 12,371 - 8,93 + 1,212; г) 14 - (3,96 + 7,85).
1230. Сколько единиц в каждом разряде числа: 32,547; 2,6034?
1231. Разложите по разрядам число:
а) 24,578;
б) 0,520001.
1232. Запишите десятичную дробь, в которой:
а) 15 целых, 3 десятых, 7 сотых и 9 тысячных;
б) 0 целых, 3 десятых, 0 сотых и 4 тысячных.
1233. Выразите длину отрезка АВ = 5 м 7 дм 6 см 2 мм:
а) в метрах; в) в сантиметрах;
б) в дециметрах; г) в миллиметрах.
Выразите длину отрезка СМ в метрах, дециметрах, сантиметрах и миллиметрах, если СМ = 4,573 м.
1234. Отметьте на координатном луче точки с координатами: 0,46; 0,8; 1,25; 0,36; 0,77; 1,47. Единичный отрезок равен 1 дм.
1235. Найдите координаты точек А, B, С, D и К (рис. 146).

1236. Зная, что 11,87 - 7,39 = 4,48, найдите значение выражения или решите уравнение:
а) 7,39 + 4,48; г) 7,39 + у = 11,87;
б) 11,87 - 4,48; д) 4,48 + z = 11,87;
в) х- 7,39 = 4,48; е) 11,87 - р = 7,39.
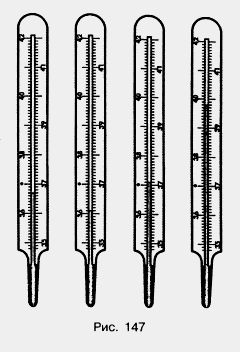
1237. Прочитайте показания термометров (рис. 147). Сколько градусов будет показывать каждый из них, если его столбик:
а) поднимется на 4 малых деления; на 2 больших деления; на 0,5°С; на 1,3°С;
б) опустится на 7 малых делений; на одно большое деление; на 0,3°С; на 1,4°С?
1238. Решите уравнение:
а)z + 3,8 = 8;
б) у - 6,5 = 12;
в) 13,5 - х = 1,8;
г)15,4 + k = 15,4;
д) 2,8 + I + 3,7 = 12,5;
е) (5,6 - г) + 3,8 = 4,4.
1239. Вычислите устно:

1240. Восстановите цепочку вычислений
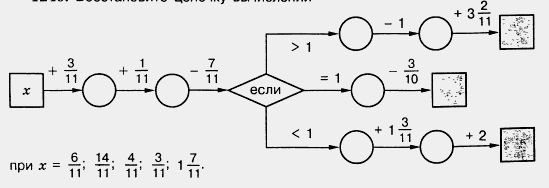
1241. Назовите какое-либо число, расположенное на координатном луче:
а) между числами 0,1 и 0,2;
б) между 0,02 и 0,03;
в) левее 0,001, но правее 0.
1242. Какую часть квадратного метра составляет:
а) 1 дм2; б) 1 см2; в) 10 дм2; г) 100 см2?
1243. Стороны треугольника 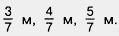 . Найдите его периметр. . Найдите его периметр.
1244. Найдите число, если 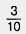 его равны: 30; 15; 6. его равны: 30; 15; 6.
1245. Какая часть периода хоккейного матча сыграна, если с начала матча прошло: 5 мин; 10 мин; 15 мин; 1 мин 20 с; 20 с? (Период продолжается 20 мин.)
1246. Сколько Буратино заплатил за арбуз, который стоил 20 сольдо и еще пол-арбуза?
1247. Сравните числа:
а) 12,567 и 125,67;
б) 7,399 и 7,4.
1248. Между какими двумя соседними натуральными числами находится число:
а) 5,1; б)6,32; в) 9,999; г) 25,257?
1249. Расставьте в порядке убывания числа: 0,915; 2,314; 0,9078; 2,316; 2,31; 10,45.
1250. Расставьте в порядке возрастания величины: 8,09 км; 8165,3 м; 8 154 257 мм; 815 376 см.
1251. Решите уравнение:
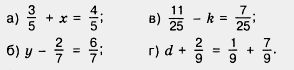
1252. Выразите:
а) в метрах: 17 м 8 см; 8 м 17 см; 4 см; 15 дм;
б) в тоннах: 3 т 8 ц 67 кг; 1244 кг; 710 кг.
1253. Решите задачу:
1) На машину погрузили 7 одинаковых мешков с мукой и 12 одинаковых мешков с крупой. Масса мешка с мукой в 2 раза больше массы мешка с крупой. Найдите массу мешка с мукой и мешка с крупой, если всего на машину погрузили 780 кг.
2) Масса индюка меньше массы овцы в 3 раза, а масса трех таких овец больше массы пяти индюков на 60 кг. Какова масса одного индюка и какова масса одной овцы?
1254. Разгадайте чайнворд, помещенный на форзаце в конце учебника.
1255. Выполните сложение:
а) 395,486 + 4,58; г) 1,9679 + 269,0121;
б) 7,6 + 908,67; д) 23,84 + 0,267;
в) 0,54 + 24,1789; е) 0,01237 + 0,0009876.
1256. Выполните вычитание:
а) 0,59 - 0,27; г) 18,01 - 2,9; ж) 7,45 - 4,45;
б) 6,05 - 2,87; д) 15 - 1,12; з) 206,48 - 90,507;
в) 3,1 - 0,09; е) 3 - 0,07; и) 0,067 - 0,00389.
1257. Одна из сторон треугольника 83,6 см, вторая на 14,8 см длиннее первой, а третья на 8,6 см длиннее второй. Найдите периметр треугольника.
1258. Трубу длиной 9,35 м разрезали на две части. Длина одной части 2,89 м. На сколько метров вторая часть длиннее первой?
1259. Воздушный шар состоит из оболочки, гондолы для пассажиров и газовой горелки для нагрева воздуха внутри оболочки. Масса гондолы 0,24 т, и она меньше массы оболочки на 0,32 т, но больше массы газовой горелки на 0,15 т. Какова масса воздушного шара?
1260. Автомашина в первый час прошла 48,3 км, во второй час — на 15,8 км меньше, чем в первый, а в третий час — на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа?
1261. Собственная скорость теплохода 40,5 км/ч, а скорость течения 5,8 км/ч. Найдите скорость теплохода по течению и против течения.
1262. Скорость катера по течению 23,7 км/ч. Найдите собственную скорость катера и его скорость против течения, если скорость течения 3,8 км/ч.
1263. Выполните действия:
а) 73,12 - (5,34 + 13,12);
б) 101,3 + (84,7 + 1,11);
в) (47,28 - 34,98) + (55,02 + 34,98);
г) (46,83 + 15,77) - (6,83 - 5,77).
1264. Разложите по разрядам числа:
41,87; 0,6098; 13,5401.
1265. Запишите десятичную дробь, в которой:
а) 21 целая, 2 десятых, 8 сотых;
б) 0 целых, 0 десятых, 3 сотых, 5 тысячных.
1266. Выразите длину отрезка АВ в метрах, дециметрах, сантиметрах и миллиметрах, если АВ = 8,906 м.
1267. Отметьте на координатном луче числа: 0,25; 0,5; 0,9; 0,37; 0,73; 1,24. За единичный отрезок примите 1 дм.
1268. Решите уравнение:
а) (х - 18,2) + 3,8 = 15,6; в) 16,5 - (t + 3,4) = 4,9;
б) 34,2 - (17,9 - у) = 22; г) г + 16,23 - 15,8 = 7,1.
1269. Объем прямоугольного параллелепипеда 84 см3. Этот параллелепипед разделили на две части. Найдите объем каждой части, если:
а) объем одной части в 6 раз больше объема другой;
б) объем одной части на 40 см3 больше объема другой.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|