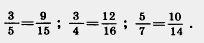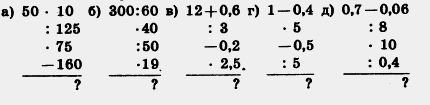|
|
|
| (2 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Основное свойство дроби</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Основное свойство дроби, круг, натуральное число, дроби, координатный луч, выражения, микрокалькуляторе, знаменатель, уравнение</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Основное свойство дроби''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Основное свойство дроби''' |
| | | | |
| - | <br> | + | <br>'''8. Основное свойство дроби''' |
| | | | |
| - | <br>''' 8. Основное свойство дроби''' | + | <br>Разделим '''[[Окружность и круг|круг]]''' на 4 равные части и 3 из них закрасим, а потом каждую четверть круга разделим еще на 5 равных частей (рис. 8). Тогда весь круг окажется разделенным на 4 • 5 = 20 частей, а в трех закрашенных четвертях круга будет 3 • 5 таких частей. Поэтому [[Image:17-07-1.jpg|240px|Задание]]<br>Это равенство можно записать и так: |
| | | | |
| - | <br>Разделим круг на 4 равные части и 3 из них закрасим, а потом каждую четверть круга разделим еще на 5 равных частей (рис. 8). Тогда весь круг окажется разделенным на 4 • 5 = 20 частей, а в трех закрашенных четвертях круга будет 3 • 5 таких<br>частей. Поэтому [[Image:17-07-1.jpg]]<br>Это равенство можно записать и так:
| + | [[Image:17-07-2.jpg|120px|Задание]]<br> <br>'''''Если числитель и знаменатель дроби умножить или разделить на одно и то же '''[[Презентація до теми Натуральний ряд чисел. Читання і запис натуральних чисел, більших за мільйон. Число 0|натуральное число]]''', го получится равная ей Рис. 8 дробь. Это свойство называют основным свойством дроби.''''' |
| | | | |
| - | [[Image:17-07-2.jpg]]<br> <br>'''''Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, го получится равная ей Рис. 8 дробь. <br>Это свойство называют основным свойством дроби.'''''
| |
| | | | |
| - | [[Image:17-07-3.jpg]]<br>Например,[[Image:17-07-4.jpg]]
| |
| | | | |
| - | '''''Две равные дроби являются различными записями одного и того же числа.''''' | + | [[Image:17-07-3.jpg|180px|Задание]] |
| | + | |
| | + | <br>Например,[[Image:17-07-4.jpg|240px|Задание]] |
| | + | |
| | + | '''''Две равные дроби являются различными записями одного и того же числа.''''' |
| | | | |
| | '''?''' Сформулируйте основное свойство дроби. Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3? | | '''?''' Сформулируйте основное свойство дроби. Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3? |
| | | | |
| - | '''К ''' 202. Используя рисунок 9, объясните, почему равны дроби: | + | '''К ''' 202. Используя рисунок 9, объясните, почему равны '''[[Фішки для допитливих до уроку: Дробові числа. Звичайні дроби.|дроби]]''': |
| | | | |
| - | [[Image:17-07-5.jpg]] | + | [[Image:17-07-5.jpg|240px|Задание]] |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:17-07-6.jpg|550px|Правило]] <br><br>203.По рис. 10 объясните, почему равны дроби: |
| | | | |
| - | [[Image:17-07-6.jpg]]<br><br> <br><br>203.По рис. 10 объясните, почему равны дроби:
| + | <br> |
| | | | |
| - | [[Image:17-07-7.jpg]]<br> <br>204. Поясните с помощью часов, почему: | + | [[Image:17-07-7.jpg|550px|Задание]]<br> <br>204. Поясните с помощью часов, почему: |
| | | | |
| - | [[Image:17-07-8.jpg]]<br><br>205. Начертите два отрезка А В и CD длиной по 8 см. Отметьте цветным карандашом [[Image:17-07-9.jpg]] отрезка АВ и [[Image:17-07-10.jpg]] отрезка CD.<br>Сравните с помощью циркуля цветные части отрезков АВ и CD. | + | [[Image:17-07-8.jpg|480px|Задание]]<br><br>205. Начертите два отрезка А В и CD длиной по 8 см. Отметьте цветным карандашом [[Image:17-07-9.jpg]] отрезка АВ и [[Image:17-07-10.jpg]] отрезка CD. |
| | | | |
| - | 206. Начертите координатный луч, приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки с координатами
| + | Сравните с помощью циркуля цветные части отрезков АВ и CD. |
| | | | |
| - | [[Image:17-07-11.jpg]] [[Image:17-07-12.jpg]] Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства. | + | 206. Начертите '''[[Порівняння натуральних чисел за допомогою координатного променя. Презентація уроку|координатный луч]]''', приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки с координатами[[Image:17-07-11.jpg|360px|Задание]] [[Image:17-07-12.jpg]] Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства. |
| | | | |
| - | 207. Умножьте числитель и знаменатель каждой дроби —1 у-. ~» ^ на 5. Напишите соответствующие равенства.<br>208. Разделите числитель и знаменатель каждой дроби<br>fi Q 1 С 0|<br>з * 6 ' 9 * 38 на ^апишите соответствующие равенства.<br>113<br>209. Сколько двенадцатых долей содержится в —, —, —,<br>JL А? 6 • з 1<br>210. Объясните, почему верно равенство:<br>v _4_ 8 . м 44 _ 11<br>5 ~ 10 * 100~" 25 •<br>211. Запишите в виде обыкновенных дробей частные: 3:8; 12:32; 20:48; 5:12. Какие из полученных дробей равны?<br>212. Какое натуральное число надо записать вместо буквы, чтобы было верным равенство:<br>v 14 х ш Лч m _ 5 . V 17 _ J_ . v 15 __5_<br>21 [[Участник:User16|User16]]3~ ' 18 ~ 9 ' ' 51 ~ п ' Г) у 6 '<br>О<br> 213. Вычислите устно:<br>а) 50 • 10 б) 300:60 в) 12 + 0,6 г) 1-0,4 д) 0,7-0,06<br>: 125 40 : 3 . 5 : 8<br>. 75 :50 -0,2 -0,5 • 10<br>-160 •19 • 2,5. : 5 : 0,4<br>? ? ? ? ?<br> <br><br>214 Какое число надо умножить на 3, чтобы получить: 3,3; 33,3; 6,6; 6,66; 0,99; 0,999?<br>215. Найдите значение выражения:<br>а) 23 + 2,6; б) 0,32 + 1Д; в) (1,6-0,7)2; г) (0,6.0,5 + 0,7)3.<br>216. На координатном луче (рис. 11) отмечены числа а и 3. Кратно ли число а трем? Отметьте на луче два общих кратных чисел а и 3.<br>0 За<br> 1 <br>Рис. 11<br>217. Найдите, использовав рисунок 12, координаты точек А, В, С и D. Есть ли среди этих точек такие, координаты которых — общие кратные чисел тип?<br> <br>В С D<br>Рис. 12<br><br>218. На сколько процентов увеличится площадь прямоугольника, если его Длину увеличить на 30%, а ширину — на 20%?<br>219. Составьте программу вычисления на микрокалькуля-<br>3 6<br>торе значения выражения: а) 2,85-(3,27 —1,45); б) - — ' —<br>5,41 -(-Ь,59<br>220. Найдите методом «решета Эратосфена» все простые числа среди первых ста натуральных чисел.<br>221. Разложите на простые множители числа: 1) 375; 8505 ; 41472; 2) 425; 4225; 8775.<br>222. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 1) 2450 и 3500; 2) 792 и 2178.<br>223. Решите задачу:<br>1) Школьники во время каникул совершили велосипедный поход. Весь путь составил 79,2 км. Первые 48,6 км они двигались со скоростью 12,15 км/ч и сделали привал на 2,5 ч, а потом ехали со скоростью 15,3 км/ч. Сколько времени они были в походе?<br>2*<br>2) Отряд партизан, выполняя боевое задание, прошел 32,4 км. Первые 4,5 ч они шли по дороге со скоростью 5,2 км/ч и сделали привал на 1,6 ч, а остальное время они шли по болотистой местности со скоростью 2,5 км/ч. Сколько времени партизаны затратили на весь переход?<br>35 <br> <br>224 Составьте задачу по выражению — -f- — .<br>225. Выполните действия: 8,12-0,25+3,24-0,25. 228. Выполните действия с помощью микрокалькулятора и округлите ответ до сотых:<br>а) 2,835:0,225-4,537 — 32,929;<br>б) (4,976+15,2473).2,14-5,0784. 227. Разделите числитель и знаменатель каждой из дробей Щ , -Ц , -Ц , Щ на 9. Напишите соответствующие<br>равенства.<br>228. Начертите координатный луч, приняв за единичный отрезок длину 12 клеток тетради. Отметьте на луче точки с координатами: 4-»-s-»T77»-ir-»T77»4-. Какие из этих чисел являются<br>4 О 12 о 1Z О<br>координатами одной и той же точки?<br>1 1 2 S<br>229. Сколько: а) шестых долей содержится в —, —, —, —;<br>л о о 6 12 3 4<br>б) пятнадцатых долей содержится в —, —, —, —?<br>О 3 5 3<br>280. Найдите наибольший общий делитель и наименьшее общее кратное чисел:<br>а) 18 и 36; б) 33 и 44; в) 378 и 441; г) 11 340 и 37 800.<br>231. Решите уравнение: а) 2,45 • (т—8,8)=4,41; б) 7,54Л-3,6Л = 5,91.<br><br> | + | 207. Умножьте числитель и знаменатель каждой дроби [[Image:17-07-13.jpg|120px|Задание]] на 5. Напишите соответствующие равенства. |
| | | | |
| - | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br>
| + | 208. Разделите числитель и знаменатель каждой дроби [[Image:17-07-14.jpg|120px|Задание]] на 3. Запишите соответствующие равенства. |
| | | | |
| - | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 6 класса [[Математика|скачать]]</sub> | + | 209. Сколько двенадцатых долей содержится в[[Image:17-07-15.jpg|80px|Задание]] [[Image:17-07-16.jpg]] |
| | + | |
| | + | 210. Объясните, почему верно равенство: |
| | + | |
| | + | [[Image:17-07-17.jpg|240px|Задание]] |
| | + | |
| | + | 211. Запишите в виде обыкновенных дробей частные: 3:8; 12:32; 20:48; 5:12. Какие из полученных дробей равны? |
| | + | |
| | + | 212. Какое натуральное число надо записать вместо буквы, чтобы было верным равенство: |
| | + | |
| | + | [[Image:17-07-18.jpg|360px|Задание]]<br><br>'''П ''' 213. Вычислите устно: |
| | + | |
| | + | [[Image:17-07-19.jpg|480px|Задание]] |
| | + | |
| | + | 214 Какое число надо умножить на 3, чтобы получить: 3,3; 33,3; 6,6; 6,66; 0,99; 0,999? |
| | + | |
| | + | 215. Найдите значение '''[[Повторення таблиць додавання і віднімання. Складання виразів за текстовим формулюванням|выражения]]''': |
| | + | |
| | + | а) 2<sup>3</sup> + 2,6; б) 0,3<sup>2</sup> + 1,1; в) (1,6-0,7)<sup>2</sup>; г) (0,6.0,5 + 0,7)<sup>3</sup>. |
| | + | |
| | + | 216. На координатном луче (рис. 11) отмечены числа а и 3. Кратно ли число а трем? Отметьте на луче два общих кратных чисел а и 3. |
| | + | |
| | + | [[Image:17-07-20.jpg|480px|Задание]]<br><br>217. Найдите, использовав рисунок 12, координаты точек А, В, С и D. Есть ли среди этих точек такие, координаты которых — общие кратные чисел m и n?<br> |
| | + | |
| | + | [[Image:17-07-21.jpg|480px|Задание]] <br><br>218. На сколько процентов увеличится площадь прямоугольника, если его Длину увеличить на 30%, а ширину — на 20%? |
| | + | |
| | + | 219. Составьте [http://xvatit.com/it/fishki-ot-itshki/ '''программу'''] вычисления на '''[[Микрокалькулятор|микрокалькуляторе]]''' значения выражения: |
| | + | |
| | + | а) 2,85 • (3,27 —1,45); |
| | + | |
| | + | [[Image:17-07-22.jpg|120px|Задание]] |
| | + | |
| | + | ''' М ''' 220. Найдите методом «решета Эратосфена» все простые числа среди первых ста натуральных чисел. |
| | + | |
| | + | 221. Разложите на простые множители числа: |
| | + | |
| | + | 1) 375; 8505 ; 41472; 2) 425; 4225; 8775. |
| | + | |
| | + | 222. Найдите наибольший общий делитель и наименьшее общее кратное чисел: |
| | + | |
| | + | 1) 2450 и 3500; 2) 792 и 2178. |
| | + | |
| | + | 223. Решите задачу: |
| | + | |
| | + | 1) Школьники во время каникул совершили велосипедный поход. Весь путь составил 79,2 км. Первые 48,6 км они двигались со скоростью 12,15 км/ч и сделали привал на 2,5 ч, а потом ехали со скоростью 15,3 км/ч. Сколько времени они были в походе? |
| | + | |
| | + | 2) Отряд партизан, выполняя боевое задание, прошел 32,4 км. Первые 4,5 ч они шли по дороге со скоростью 5,2 км/ч и сделали привал на 1,6 ч, а остальное время они шли по болотистой местности со скоростью 2,5 км/ч. Сколько времени партизаны затратили на весь переход? |
| | + | |
| | + | 224 Составьте задачу по выражению [[Image:17-07-23.jpg|80px|Задание]]. |
| | + | |
| | + | 225. Выполните действия: 8,12 • 0,25+3,24 • 0,25. |
| | + | |
| | + | 226. Выполните действия с помощью микрокалькулятора и округлите ответ до сотых: |
| | + | |
| | + | а) 2,835:0,225 • 4,537 — 32,929;<br>б) (4,976+15,2473) • 2,14-5,0784. |
| | + | |
| | + | '''Д ''' 227. Разделите числитель и '''[[Задачі до уроку на тему «Зведення дробів до спільного знаменника. Порівняння дробів»|знаменатель]]''' каждой из дробей [[Image:17-07-24.jpg|120px|Задание]] на 9. Напишите соответствующие равенства. |
| | + | |
| | + | 228. Начертите координатный луч, приняв за единичный отрезок длину 12 клеток тетради. Отметьте на луче точки с координатами: [[Image:17-07-25.jpg|180px|Задание]] Какие из этих чисел являются координатами одной и той же точки? |
| | + | |
| | + | 229. Сколько: |
| | + | |
| | + | а) шестых долей содержится в [[Image:17-07-26.jpg|120px|Задание]]<br>б) пятнадцатых долей содержится в [[Image:17-07-27.jpg|120px|Задание]] |
| | + | |
| | + | 280. Найдите наибольший общий делитель и наименьшее общее кратное чисел: |
| | + | |
| | + | а) 18 и 36; б) 33 и 44; в) 378 и 441; г) 11 340 и 37 800. |
| | + | |
| | + | 231. Решите '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''': |
| | + | |
| | + | а) 2,45 • (m—8,8)=4,41; |
| | + | |
| | + | б) 7,54k-3,6k = 5,91.<br> |
| | + | |
| | + | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> |
| | | | |
| | <br> | | <br> |
| | + | |
| | + | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 6 класса [[Математика|скачать]]</sub><br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 09:48, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Основное свойство дроби
8. Основное свойство дроби
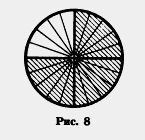
Разделим круг на 4 равные части и 3 из них закрасим, а потом каждую четверть круга разделим еще на 5 равных частей (рис. 8). Тогда весь круг окажется разделенным на 4 • 5 = 20 частей, а в трех закрашенных четвертях круга будет 3 • 5 таких частей. Поэтому 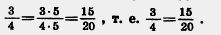
Это равенство можно записать и так:
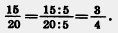
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, го получится равная ей Рис. 8 дробь. Это свойство называют основным свойством дроби.
Например,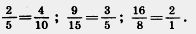
Две равные дроби являются различными записями одного и того же числа.
? Сформулируйте основное свойство дроби. Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3?
К 202. Используя рисунок 9, объясните, почему равны дроби:
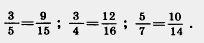
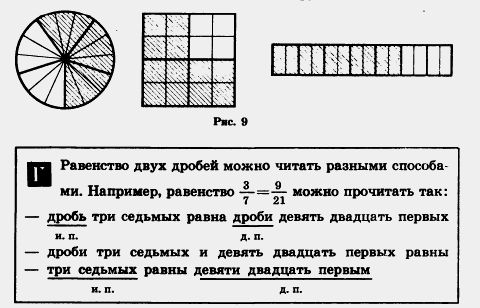
203.По рис. 10 объясните, почему равны дроби:
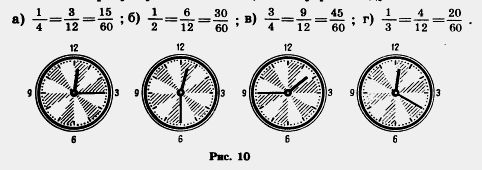
204. Поясните с помощью часов, почему:
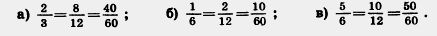
205. Начертите два отрезка А В и CD длиной по 8 см. Отметьте цветным карандашом 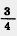 отрезка АВ и отрезка АВ и 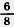 отрезка CD. отрезка CD.
Сравните с помощью циркуля цветные части отрезков АВ и CD.
206. Начертите координатный луч, приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки с координатами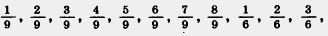 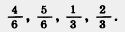 Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства. Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства.
207. Умножьте числитель и знаменатель каждой дроби 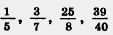 на 5. Напишите соответствующие равенства. на 5. Напишите соответствующие равенства.
208. Разделите числитель и знаменатель каждой дроби 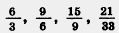 на 3. Запишите соответствующие равенства. на 3. Запишите соответствующие равенства.
209. Сколько двенадцатых долей содержится в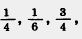 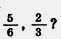
210. Объясните, почему верно равенство:

211. Запишите в виде обыкновенных дробей частные: 3:8; 12:32; 20:48; 5:12. Какие из полученных дробей равны?
212. Какое натуральное число надо записать вместо буквы, чтобы было верным равенство:
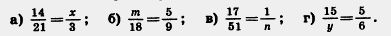
П 213. Вычислите устно:
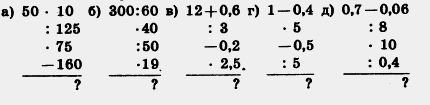
214 Какое число надо умножить на 3, чтобы получить: 3,3; 33,3; 6,6; 6,66; 0,99; 0,999?
215. Найдите значение выражения:
а) 23 + 2,6; б) 0,32 + 1,1; в) (1,6-0,7)2; г) (0,6.0,5 + 0,7)3.
216. На координатном луче (рис. 11) отмечены числа а и 3. Кратно ли число а трем? Отметьте на луче два общих кратных чисел а и 3.

217. Найдите, использовав рисунок 12, координаты точек А, В, С и D. Есть ли среди этих точек такие, координаты которых — общие кратные чисел m и n?

218. На сколько процентов увеличится площадь прямоугольника, если его Длину увеличить на 30%, а ширину — на 20%?
219. Составьте программу вычисления на микрокалькуляторе значения выражения:
а) 2,85 • (3,27 —1,45);
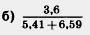
М 220. Найдите методом «решета Эратосфена» все простые числа среди первых ста натуральных чисел.
221. Разложите на простые множители числа:
1) 375; 8505 ; 41472; 2) 425; 4225; 8775.
222. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
1) 2450 и 3500; 2) 792 и 2178.
223. Решите задачу:
1) Школьники во время каникул совершили велосипедный поход. Весь путь составил 79,2 км. Первые 48,6 км они двигались со скоростью 12,15 км/ч и сделали привал на 2,5 ч, а потом ехали со скоростью 15,3 км/ч. Сколько времени они были в походе?
2) Отряд партизан, выполняя боевое задание, прошел 32,4 км. Первые 4,5 ч они шли по дороге со скоростью 5,2 км/ч и сделали привал на 1,6 ч, а остальное время они шли по болотистой местности со скоростью 2,5 км/ч. Сколько времени партизаны затратили на весь переход?
224 Составьте задачу по выражению 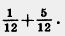 . .
225. Выполните действия: 8,12 • 0,25+3,24 • 0,25.
226. Выполните действия с помощью микрокалькулятора и округлите ответ до сотых:
а) 2,835:0,225 • 4,537 — 32,929;
б) (4,976+15,2473) • 2,14-5,0784.
Д 227. Разделите числитель и знаменатель каждой из дробей 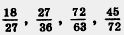 на 9. Напишите соответствующие равенства. на 9. Напишите соответствующие равенства.
228. Начертите координатный луч, приняв за единичный отрезок длину 12 клеток тетради. Отметьте на луче точки с координатами: 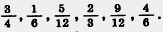 Какие из этих чисел являются координатами одной и той же точки? Какие из этих чисел являются координатами одной и той же точки?
229. Сколько:
а) шестых долей содержится в 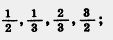
б) пятнадцатых долей содержится в 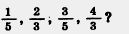
280. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
а) 18 и 36; б) 33 и 44; в) 378 и 441; г) 11 340 и 37 800.
231. Решите уравнение:
а) 2,45 • (m—8,8)=4,41;
б) 7,54k-3,6k = 5,91.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Планирование по математике , учебники и книги онлайн, курсы и задачи по математике для 6 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|