Основные результаты-4 (8 класс) — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Основные результаты-4 (8 класс)

 		Версия 09:06, 8 октября 2012 (просмотреть исходный код)
User17  (Обсуждение | вклад)
← Предыдущая правка
		Текущая версия на 10:58, 8 октября 2012 (просмотреть исходный код)
User17  (Обсуждение | вклад) 
 
		
(2 промежуточные версии не показаны)
Строка 7:
Строка 7:
 '''Основные результаты'''    '''Основные результаты'''  
  
- <br><u>'''В этой главе вы познакомились с новыми терминами математического языка''': </u> + <br><u>'''В этой главе вы познакомились с новыми терминами математического языка''': </u>  
  
- '''[[Презентація уроку на тему "Квадратні рівняння. Теорема Вієта"|квадратное уравнение]]'''; <br>старший коэффициент, второй коэффициент, свободный член (для квадратного уравнения); <br>полное квадратное уравнение, неполное квадратное уравнение; <br>неприведенное квадратное уравнение, приведенное квадратное уравнение; <br>корень квадратного уравнения (квадратного трехчлена); <br>дискриминант квадратного уравнения (квадратного трехчлена); <br>рациональное уравнение; <br>биквадратное уравнение; <br>'''[[иррациональное уравнение|Иррациональные уравнения]]'''; <br>параметр, уравнение с параметром; <br>посторонний корень (для рационального или иррационального уравнения); <br>равносильные уравнения; <br>равносильные и неравносильные преобразования уравнения.   + '''[[Презентація уроку: Квадратні рівняння|квадратное уравнение]]'''; <br>старший коэффициент, второй коэффициент, свободный член (для квадратного уравнения); <br>полное квадратное уравнение, неполное квадратное уравнение; <br>неприведенное квадратное уравнение, приведенное квадратное уравнение; <br>корень квадратного уравнения (квадратного трехчлена); <br>дискриминант квадратного уравнения (квадратного трехчлена); <br>рациональное уравнение; <br>биквадратное уравнение; <br>'''[[Иррациональные уравнения|иррациональные уравнения]]'''; <br>параметр, уравнение с параметром; <br>посторонний корень (для рационального или иррационального уравнения); <br>равносильные уравнения; <br>равносильные и неравносильные преобразования уравнения.  
  
  + <br> 
  
-   + <u>'''Мы вывели формулы:''' </u>  
- <u>'''Мы вывели формулы:''' </u> + 
  
 корней квадратного уравнения ах<sup>2</sup> + bх + с = 0:    корней квадратного уравнения ах<sup>2</sup> + bх + с = 0:  
Строка 23:
Строка 23:
 разложения на множители квадратного трехчлена: <br>ах<sup>2</sup> + bх + с- а(х - х<sup>1</sup>)(х- х<sup>2</sup>), где х<sub>1</sub>г х<sub>2</sub> — '''[[Степени и корни. Степенные функции. Основные результаты|корни]]''' квадратного трехчлена.    разложения на множители квадратного трехчлена: <br>ах<sup>2</sup> + bх + с- а(х - х<sup>1</sup>)(х- х<sup>2</sup>), где х<sub>1</sub>г х<sub>2</sub> — '''[[Степени и корни. Степенные функции. Основные результаты|корни]]''' квадратного трехчлена.  
  
-   + <br> 
  
 <u>'''Мы сформулировали и доказали теоремы'''</u> о связи числа корней квадратного уравнения ах<sup>2</sup> + bх + с = 0 с его дискриминантом D - b<sup>2</sup> = 4ас и о связи корней <br>уравнения с его коэффициентами: <br>если D &lt; 0, то уравнение не имеет корней; <br>если D = 0, то уравнение имеет один корень (или, что <br>то же самое, два одинаковых корня); <br>если D &gt; 0, то уравнение имеет два различных корня; <br>если х<sub>1</sub> и х<sub>2</sub> — корни уравнения, то [[Image:13-06-83.jpg|320px|Теорема Виета]]&nbsp; <br>Для приведенного уравнения х<sup>2</sup> + рх + q = 0 эти соотношения имеют вид    <u>'''Мы сформулировали и доказали теоремы'''</u> о связи числа корней квадратного уравнения ах<sup>2</sup> + bх + с = 0 с его дискриминантом D - b<sup>2</sup> = 4ас и о связи корней <br>уравнения с его коэффициентами: <br>если D &lt; 0, то уравнение не имеет корней; <br>если D = 0, то уравнение имеет один корень (или, что <br>то же самое, два одинаковых корня); <br>если D &gt; 0, то уравнение имеет два различных корня; <br>если х<sub>1</sub> и х<sub>2</sub> — корни уравнения, то [[Image:13-06-83.jpg|320px|Теорема Виета]]&nbsp; <br>Для приведенного уравнения х<sup>2</sup> + рх + q = 0 эти соотношения имеют вид  
  
- x<sub>1</sub> = x<sub>2</sub> = - p; x<sub>1</sub>x<sub>2</sub> = q + x<sub>1</sub> = x<sub>2</sub> = - p; x<sub>1</sub>x<sub>2</sub> = q  
  
- <br><u>'''Мы выработали алгоритмы:'''</u> + <br><u>'''Мы выработали алгоритмы:'''</u>  
  
 решения квадратного уравнения; <br>решения '''[[Рациональные уравнения|рационального уравнения]]'''. <br><br>    решения квадратного уравнения; <br>решения '''[[Рациональные уравнения|рационального уравнения]]'''. <br><br>  
  
- ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' + ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''  
  
 <br>    <br>  
Текущая версия на 10:58, 8 октября 2012
 
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Основные результаты-4 (8 класс) 

 
Основные результаты 

В этой главе вы познакомились с новыми терминами математического языка:  
квадратное уравнение; 
старший коэффициент, второй коэффициент, свободный член (для квадратного уравнения); 
полное квадратное уравнение, неполное квадратное уравнение; 
неприведенное квадратное уравнение, приведенное квадратное уравнение; 
корень квадратного уравнения (квадратного трехчлена); 
дискриминант квадратного уравнения (квадратного трехчлена); 
рациональное уравнение; 
биквадратное уравнение; 
иррациональные уравнения; 
параметр, уравнение с параметром; 
посторонний корень (для рационального или иррационального уравнения); 
равносильные уравнения; 
равносильные и неравносильные преобразования уравнения. 

 
Мы вывели формулы:  
корней квадратного уравнения ах² + bх + с = 0: 

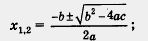
корней квадратного уравнения ах² + 2kx + с = 0: 
 
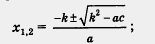
разложения на множители квадратного трехчлена: 
ах² + bх + с- а(х - х¹)(х- х²), где х₁г х₂ — корни квадратного трехчлена. 

 
Мы сформулировали и доказали теоремы о связи числа корней квадратного уравнения ах² + bх + с = 0 с его дискриминантом D - b² = 4ас и о связи корней 
уравнения с его коэффициентами: 
если D < 0, то уравнение не имеет корней; 
если D = 0, то уравнение имеет один корень (или, что 
то же самое, два одинаковых корня); 
если D > 0, то уравнение имеет два различных корня; 
если х₁ и х₂ — корни уравнения, то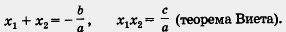   
Для приведенного уравнения х² + рх + q = 0 эти соотношения имеют вид 
x₁ = x₂ = - p; x₁x₂ = q 

Мы выработали алгоритмы: 
решения квадратного уравнения; 
решения рационального уравнения. 

 
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.  

 
_{онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать} 

 

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%9E%D1%81%D0%BD%D0%BE%D0%B2%D0%BD%D1%8B%D0%B5_%D1%80%D0%B5%D0%B7%D1%83%D0%BB%D1%8C%D1%82%D0%B0%D1%82%D1%8B-4_(8_%D0%BA%D0%BB%D0%B0%D1%81%D1%81)»
@@ Строка 7: / Строка 7: @@
 '''Основные результаты'''
 <br><u>'''В этой главе вы познакомились с новыми терминами математического языка''': </u>
-'''[[Презентація уроку на тему "Квадратні рівняння. Теорема Вієта"|квадратное уравнение]]'''; <br>старший коэффициент, второй коэффициент, свободный член (для квадратного уравнения); <br>полное квадратное уравнение, неполное квадратное уравнение; <br>неприведенное квадратное уравнение, приведенное квадратное уравнение; <br>корень квадратного уравнения (квадратного трехчлена); <br>дискриминант квадратного уравнения (квадратного трехчлена); <br>рациональное уравнение; <br>биквадратное уравнение; <br>'''[[иррациональное уравнение|Иррациональные уравнения]]'''; <br>параметр, уравнение с параметром; <br>посторонний корень (для рационального или иррационального уравнения); <br>равносильные уравнения; <br>равносильные и неравносильные преобразования уравнения.
+'''[[Презентація уроку: Квадратні рівняння|квадратное уравнение]]'''; <br>старший коэффициент, второй коэффициент, свободный член (для квадратного уравнения); <br>полное квадратное уравнение, неполное квадратное уравнение; <br>неприведенное квадратное уравнение, приведенное квадратное уравнение; <br>корень квадратного уравнения (квадратного трехчлена); <br>дискриминант квадратного уравнения (квадратного трехчлена); <br>рациональное уравнение; <br>биквадратное уравнение; <br>'''[[Иррациональные уравнения|иррациональные уравнения]]'''; <br>параметр, уравнение с параметром; <br>посторонний корень (для рационального или иррационального уравнения); <br>равносильные уравнения; <br>равносильные и неравносильные преобразования уравнения.
+<br>
+<u>'''Мы вывели формулы:''' </u>
-<u>'''Мы вывели формулы:''' </u>
 корней квадратного уравнения ах<sup>2</sup> + bх + с = 0:
@@ Строка 23: / Строка 23: @@
 разложения на множители квадратного трехчлена: <br>ах<sup>2</sup> + bх + с- а(х - х<sup>1</sup>)(х- х<sup>2</sup>), где х<sub>1</sub>г х<sub>2</sub> — '''[[Степени и корни. Степенные функции. Основные результаты|корни]]''' квадратного трехчлена.
+<br>
 <u>'''Мы сформулировали и доказали теоремы'''</u> о связи числа корней квадратного уравнения ах<sup>2</sup> + bх + с = 0 с его дискриминантом D - b<sup>2</sup> = 4ас и о связи корней <br>уравнения с его коэффициентами: <br>если D &lt; 0, то уравнение не имеет корней; <br>если D = 0, то уравнение имеет один корень (или, что <br>то же самое, два одинаковых корня); <br>если D &gt; 0, то уравнение имеет два различных корня; <br>если х<sub>1</sub> и х<sub>2</sub> — корни уравнения, то [[Image:13-06-83.jpg|320px|Теорема Виета]]&nbsp; <br>Для приведенного уравнения х<sup>2</sup> + рх + q = 0 эти соотношения имеют вид
 x<sub>1</sub> = x<sub>2</sub> = - p; x<sub>1</sub>x<sub>2</sub> = q
 <br><u>'''Мы выработали алгоритмы:'''</u>
 решения квадратного уравнения; <br>решения '''[[Рациональные уравнения|рационального уравнения]]'''. <br><br>
 ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''
 <br>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: