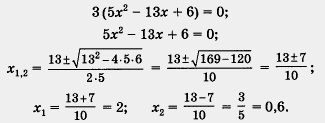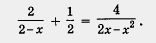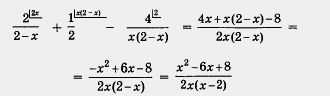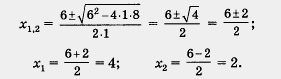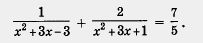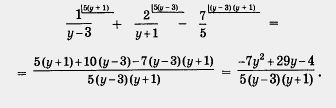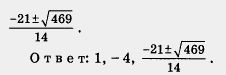|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Рациональные уравнения</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Рациональные уравнения, рациональное, линейному уравнению, дроби, корней, алгоритмом, знаменателе, формулы, переменной</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Рациональные уравнения''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Рациональные уравнения''' |
| Строка 7: |
Строка 7: |
| | <br>'''1. Алгоритм решения рационального уравнения''' | | <br>'''1. Алгоритм решения рационального уравнения''' |
| | | | |
| - | Термин «рациональное уравнение» мы ввели выше в § 7. Сначала напомним, что такое рациональное выражение. Это — алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.<br> | + | Термин «'''[[Задачі на тему «Координатна пряма. Раціональні числа»|рациональное]]''' уравнение» мы ввели выше в § 7. Сначала напомним, что такое рациональное выражение. Это — алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.<br> |
| | | | |
| | Если r(х) — рациональное выражение, то уравнение r(х) = 0 называют рациональным уравнением. <br> | | Если r(х) — рациональное выражение, то уравнение r(х) = 0 называют рациональным уравнением. <br> |
| Строка 13: |
Строка 13: |
| | Впрочем, на практике удобнее пользоваться несколько более широким толкованием термина «рациональное уравнение»: это уравнение вида h(x) = q(x), где h(x) и q(x) — рациональные выражения. <br> | | Впрочем, на практике удобнее пользоваться несколько более широким толкованием термина «рациональное уравнение»: это уравнение вида h(x) = q(x), где h(x) и q(x) — рациональные выражения. <br> |
| | | | |
| - | До сих пор мы могли решить не любое рациональное уравнение, а только такое, которое в результате различных преобразований и рассуждений сводилось к линейному уравнению. Теперь наши возможности значительно больше: мы сумеем решить рациональное уравнение, которое сводится не только к линейно- <br>му, но и к квадратному уравнению. <br> | + | До сих пор мы могли решить не любое рациональное уравнение, а только такое, которое в результате различных преобразований и рассуждений сводилось к '''[[Розв'язування системи лінійних рівнянь з двома змінними способом додавання|линейному уравнению]]'''. Теперь наши возможности значительно больше: мы сумеем решить рациональное уравнение, которое сводится не только к линейно- <br>му, но и к квадратному уравнению. <br> |
| | | | |
| | Напомним, как мы решали рациональные уравнения раньше, и попробуем сформулировать алгоритм решения. <br> | | Напомним, как мы решали рациональные уравнения раньше, и попробуем сформулировать алгоритм решения. <br> |
| Строка 19: |
Строка 19: |
| | '''Пример 1.''' Решить уравнение <br> | | '''Пример 1.''' Решить уравнение <br> |
| | | | |
| - | <img src="/images/f/fa/13-06-54.jpg" _fck_mw_filename="13-06-54.jpg" alt="" /><br><br>
| + | [[Image:13-06-54.jpg|120px|Уравнение]]<br><br> |
| | | | |
| | Решение. Перепишем уравнение в виде | | Решение. Перепишем уравнение в виде |
| | | | |
| - | <img src="/images/f/fa/13-06-54.jpg" _fck_mw_filename="13-06-54.jpg" alt="" /> = 0<br><br>При этом, как обычно, мы пользуемся тем, что равенства А = В и А - В = 0 выражают одну и ту же зависимость между А и В. Это и позволило нам перенести член <img src="/images/8/8d/13-06-55.jpg" _fck_mw_filename="13-06-55.jpg" alt="" /> в левую часть уравнения с противоположным знаком.
| + | [[Image:13-06-54.jpg|120px|Уравнение]] = 0<br><br>При этом, как обычно, мы пользуемся тем, что равенства А = В и А - В = 0 выражают одну и ту же зависимость между А и В. Это и позволило нам перенести член [[Image:13-06-55.jpg]] в левую часть уравнения с противоположным знаком. |
| | | | |
| | Выполним преобразования левой части уравнения. Имеем | | Выполним преобразования левой части уравнения. Имеем |
| | | | |
| - | <img src="/images/2/23/13-06-56.jpg" _fck_mw_filename="13-06-56.jpg" alt="" />
| + | [[Image:13-06-56.jpg|480px|Уравнение]]<br>Вспомним условия равенства '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|дроби]]''' нулю:[[Image:13-06-57.jpg|Дробь]] тогда, и только тогда, когда одновременно выполняются два соотношения: |
| | | | |
| - | <br>Вспомним условия равенства дроби нулю:<img src="/images/f/fb/13-06-57.jpg" _fck_mw_filename="13-06-57.jpg" alt="" /> тогда, и только тогда, когда одновременно выполняются два соотношения:
| + | 1) числитель дроби равен нулю (а = 0); 2) знаменатель дроби отличен от нуля [[Image:13-06-58.jpg]]). <br>Приравняв нулю числитель дроби в левой части уравнения (1), получим |
| | | | |
| - | 1) числитель дроби равен нулю (а = 0); 2) знаменатель дроби отличен от нуля <img src="/images/e/eb/13-06-58.jpg" _fck_mw_filename="13-06-58.jpg" alt="" />). <br>Приравняв нулю числитель дроби в левой части уравнения (1), получим
| + | <br> |
| | | | |
| - | <img src="/images/7/71/13-06-59.jpg" _fck_mw_filename="13-06-59.jpg" alt="" /><br><br>Осталось проверить выполнение второго указанного выше условия. Соотношение <img src="/images/e/eb/13-06-58.jpg" _fck_mw_filename="13-06-58.jpg" alt="" /> означает для уравнения (1), что <img src="/images/3/3f/13-06-60.jpg" _fck_mw_filename="13-06-60.jpg" alt="" />. Значения х<sub>1</sub> = 2 и х<sub>2</sub> = 0,6 <br>указанным соотношениям удовлетворяют и потому служат корнями уравнения (1), а вместе с тем и корнями заданного уравнения. <br>Ответ: 2; 0,6.
| + | [[Image:13-06-59.jpg|480px|Уравнение]]<br><br>Осталось проверить выполнение второго указанного выше условия. Соотношение [[Image:13-06-58.jpg|Соотношение ]] означает для уравнения (1), что [[Image:13-06-60.jpg|Соотношение ]]. Значения х<sub>1</sub> = 2 и х<sub>2</sub> = 0,6 указанным соотношениям удовлетворяют и потому служат корнями уравнения (1), а вместе с тем и корнями заданного уравнения. <br> |
| | | | |
| - | Если среди корней числителя окажется число, при котором знаменатель дроби обращается в нуль, то такое число корнем уравнения быть не может, его называют посторонним корнем и в ответ не включают. <br>Опираясь на решенный пример, сформулируем следующий алгоритм. | + | Ответ: 2; 0,6. |
| | + | |
| | + | Если среди '''[[Степени и корни. Степенные функции. Основные результаты|корней]]''' числителя окажется число, при котором знаменатель дроби обращается в нуль, то такое число корнем уравнения быть не может, его называют посторонним корнем и в ответ не включают. <br> |
| | + | |
| | + | Опираясь на решенный пример, сформулируем следующий алгоритм. |
| | | | |
| | <br>'''Алгоритм решения рационального уравнения ''' | | <br>'''Алгоритм решения рационального уравнения ''' |
| | | | |
| - | <img src="/images/d/de/13-06-69.jpg" _fck_mw_filename="13-06-69.jpg" alt="" /><br>
| + | [[Image:13-06-69.jpg|480px|Алгоритм решения рационального уравнения ]]<br> |
| | | | |
| | <br>'''Пример 2'''. Решить уравнение | | <br>'''Пример 2'''. Решить уравнение |
| | | | |
| - | <img src="/images/7/7d/13-06-68.jpg" _fck_mw_filename="13-06-68.jpg" alt="" /><sup><br></sup><br>Решение. Будем действовать в соответствии с алгоритмом. <br>1) Преобразуем уравнение к виду
| + | [[Image:13-06-68.jpg|180px|Уравнение]]<sup><br></sup><br>Решение. Будем действовать в соответствии с '''[[Урок 4. Программа действий. Алгоритм|алгоритмом]]'''. <br> |
| | | | |
| - | <img src="/images/e/e5/13-06-63.jpg" _fck_mw_filename="13-06-63.jpg" alt="" /><br><br>2) Выполним преобразования левой части этого уравнения:
| + | 1) Преобразуем уравнение к виду |
| | | | |
| - | <img src="/images/8/83/13-06-64.jpg" _fck_mw_filename="13-06-64.jpg" alt="" /><br><br>(одновременно изменили знаки в числителе и знаменателе <br>дроби). <br>Таким образом, заданное уравнение принимает вид
| + | [[Image:13-06-63.jpg|180px|Уравнение]]<br><br>2) Выполним преобразования левой части этого уравнения: |
| | | | |
| - | <img src="/images/f/fb/13-06-65.jpg" _fck_mw_filename="13-06-65.jpg" alt="" /><br><br>3) Решим уравнение х<sup>2</sup> - 6x + 8 = 0. Находим
| + | [[Image:13-06-64.jpg|320px|Уравнение]]<br><br>(одновременно изменили знаки в числителе и '''[[Задачі до уроку на тему «Зведення дробів до спільного знаменника. Порівняння дробів»|знаменателе]]''' <br>дроби). <br>Таким образом, заданное уравнение принимает вид |
| | | | |
| - | <img src="/images/a/ac/13-06-66.jpg" _fck_mw_filename="13-06-66.jpg" alt="" /><br><br>4) Для найденных значений проверим выполнение условия <img src="/images/f/f5/13-06-67.jpg" _fck_mw_filename="13-06-67.jpg" alt="" />. Число 4 этому условию удовлетворяет, а число 2 — нет. Значит, 4 — корень заданного уравнения, а 2 — посторонний корень. <br>О т в е т: 4.
| + | [[Image:13-06-65.jpg|Уравнение]]<br><br>3) Решим уравнение х<sup>2</sup> - 6x + 8 = 0. Находим |
| | + | |
| | + | [[Image:13-06-66.jpg|320px|Уравнение]]<br><br>4) Для найденных значений проверим выполнение условия [[Image:13-06-67.jpg]]. Число 4 этому условию удовлетворяет, а число 2 — нет. Значит, 4 — корень заданного уравнения, а 2 — посторонний корень. <br>О т в е т: 4. |
| | | | |
| | '''2. Решение рациональных уравнений методом введения новой переменной''' | | '''2. Решение рациональных уравнений методом введения новой переменной''' |
| Строка 63: |
Строка 69: |
| | у<sup>2</sup> + у - 20 = 0. | | у<sup>2</sup> + у - 20 = 0. |
| | | | |
| - | Это — квадратное уравнение, корни которого найдем, используя известные формулы; получим у<sub>1</sub> = 4, у<sub>2</sub> = - 5. <br>Но у = х<sup>2</sup>, значит, задача свелась к решению двух уравнений: <br>x<sup>2</sup>=4; х<sup>2</sup>=-5. | + | Это — квадратное уравнение, корни которого найдем, используя известные '''[[Формулы сокращенного умножения|формулы]]'''; получим у<sub>1</sub> = 4, у<sub>2</sub> = - 5. <br>Но у = х<sup>2</sup>, значит, задача свелась к решению двух уравнений: <br>x<sup>2</sup>=4; х<sup>2</sup>=-5. |
| | | | |
| - | Из первого уравнения находим <img src="/images/1/1c/13-06-70.jpg" _fck_mw_filename="13-06-70.jpg" alt="" /> второе уравнение не имеет корней. <br>Ответ: <img src="/images/4/48/13-06-71.jpg" _fck_mw_filename="13-06-71.jpg" alt="" />. <br>Уравнение вида ах<sup>4</sup> + bx<sup>2</sup> +c<sup> </sup> = 0 называют биквадратным уравнением («би» — два, т. е. как бы «дважды квадратное» уравнение ). Только что решенное уравнение было именно биквадратным. Любое биквадратное уравнение решается так же, как уравнение из примера 3: вводят новую переменную у = х<sup>2</sup>, решают полученное квадратное уравнение относительно переменной у, а затем возвращаются к переменной х. | + | Из первого уравнения находим [[Image:13-06-70.jpg|Решение]] второе уравнение не имеет корней. <br>Ответ: [[Image:13-06-71.jpg]]. <br>Уравнение вида ах<sup>4</sup> + bx<sup>2</sup> +c<sup> </sup> = 0 называют биквадратным уравнением («би» — два, т. е. как бы «дважды квадратное» уравнение ). Только что решенное уравнение было именно биквадратным. Любое биквадратное уравнение решается так же, как уравнение из примера 3: вводят новую переменную у = х<sup>2</sup>, решают полученное квадратное уравнение относительно переменной у, а затем возвращаются к переменной х. |
| | | | |
| | '''Пример 4.''' Решить уравнение | | '''Пример 4.''' Решить уравнение |
| | | | |
| - | <img src="/images/2/2d/13-06-72.jpg" _fck_mw_filename="13-06-72.jpg" alt="" /><br><br>Решение. Заметим, что здесь дважды встречается одно и то же выражение х<sup>2</sup> + Зх. Значит, имеет смысл ввести новую переменную у = х<sup>2</sup> + Зх. Это позволит переписать уравнение в более простом и приятном виде (что, собственно говоря, и составляет цель введения новой переменной — и запись упроща <br>ется, и структура уравнения становится более ясной):
| + | [[Image:13-06-72.jpg|240px|Уравнение]]<br><br>Решение. Заметим, что здесь дважды встречается одно и то же выражение х<sup>2</sup> + Зх. Значит, имеет смысл ввести новую переменную у = х<sup>2</sup> + Зх. Это позволит переписать уравнение в более простом и приятном виде (что, собственно говоря, и составляет цель введения новой '''[[Линейное уравнение с двумя переменными и его график|переменной]]''' — и запись упроща <br>ется, и структура уравнения становится более ясной): |
| | | | |
| - | <img src="/images/9/9d/13-06-73.jpg" _fck_mw_filename="13-06-73.jpg" alt="" /><br><br>А теперь воспользуемся алгоритмом решения рационального уравнения.
| + | [[Image:13-06-73.jpg|120px|Уравнение]]<br><br>А теперь воспользуемся алгоритмом решения рационального уравнения. |
| | | | |
| | 1) Перенесем все члены уравнения в одну часть: | | 1) Перенесем все члены уравнения в одну часть: |
| | | | |
| - | <img src="/images/9/9d/13-06-73.jpg" _fck_mw_filename="13-06-73.jpg" alt="" /> = 0<br>12 7 <br>2) Преобразуем левую часть уравнения
| + | [[Image:13-06-73.jpg|120px|Уравнение]] = 0<br>2) Преобразуем левую часть уравнения |
| | | | |
| - | <img src="/images/d/d6/13-06-74.jpg" _fck_mw_filename="13-06-74.jpg" alt="" /><br><br>Итак, мы преобразовали заданное уравнение к виду
| + | [[Image:13-06-74.jpg|320px|Уравнение]]<br><br>Итак, мы преобразовали заданное уравнение к виду |
| | | | |
| - | <img src="/images/9/98/13-06-75.jpg" _fck_mw_filename="13-06-75.jpg" alt="" /><br><br>3) Из уравнения - 7у<sup>2</sup> + 29у -4 = 0 находим у<img src="/images/7/7c/13-06-76.jpg" _fck_mw_filename="13-06-76.jpg" alt="" /> (мы с вами уже решили довольно много квадратных уравнений, так что всегда приводить в учебнике подробные выкладки, наверное, не стоит).
| + | [[Image:13-06-75.jpg|120px|Уравнение]]<br>3) Из уравнения - 7у<sup>2</sup> + 29у -4 = 0 находим [[Image:13-06-76.jpg|Решение]] (мы с вами уже решили довольно много квадратных уравнений, так что всегда приводить в учебнике подробные выкладки, наверное, не стоит). |
| | | | |
| - | 4) Выполним проверку найденных корней с помощью условия 5 (у - 3) (у + 1)<img src="/images/7/71/13-06-77.jpg" _fck_mw_filename="13-06-77.jpg" alt="" />. Оба корня этому условию удовлетворяют. <br>Итак, квадратное уравнение относительно новой переменной у решено: <img src="/images/7/7e/13-06-78.jpg" _fck_mw_filename="13-06-78.jpg" alt="" /><br>Поскольку у = х<sup>2</sup> + Зх, а у, как мы установили, принимает два значения: 4 и <img src="/images/1/1e/13-06-79.jpg" _fck_mw_filename="13-06-79.jpg" alt="" /> , — нам еще предстоит решить два уравнения: х<sup>2</sup> + Зх = 4; х<sup>2</sup> + Зх = <img src="/images/1/1e/13-06-79.jpg" _fck_mw_filename="13-06-79.jpg" alt="" /> . Корнями первого уравнения являются числа 1 и - 4, корнями второго уравнения — числа | + | 4) Выполним проверку найденных корней с помощью условия 5 (у - 3) (у + 1)[[Image:13-06-77.jpg]]. Оба корня этому условию удовлетворяют. <br>Итак, квадратное уравнение относительно новой переменной у решено: [[Image:13-06-78.jpg|Решение]]<br>Поскольку у = х<sup>2</sup> + Зх, а у, как мы установили, принимает два значения: 4 и [[Image:13-06-79.jpg]], — нам еще предстоит решить два уравнения: х<sup>2</sup> + Зх = 4; х<sup>2</sup> + Зх = [[Image:13-06-79.jpg]]. Корнями первого уравнения являются числа 1 и - 4, корнями второго уравнения — числа |
| | | | |
| - | <img src="/images/8/86/13-06-80.jpg" _fck_mw_filename="13-06-80.jpg" alt="" /><br><br>В рассмотренных примерах метод введения новой переменной был, как любят выражаться математики, адекватен ситуации, т. е. хорошо ей соответствовал. Почему? Да потому, что одно и то же выражение яйно встречалось в записи уравнения несколько раз и был резон обозначить это выражение новой <br>буквой. Но так бывает не всегда, иногда новая переменная «проявляется» только в процессе преобразований. Именно так будет обстоять дело в следующем примере.
| + | [[Image:13-06-80.jpg|240px|Решение]]<br><br>В рассмотренных примерах метод введения новой переменной был, как любят выражаться математики, адекватен ситуации, т. е. хорошо ей соответствовал. Почему? Да потому, что одно и то же выражение явно встречалось в записи уравнения несколько раз и был резон обозначить это выражение новой буквой. Но так бывает не всегда, иногда новая переменная «проявляется» только в процессе преобразований. Именно так будет обстоять дело в следующем примере. |
| | | | |
| | '''Пример 5.''' Решить уравнение <br>х(х- 1)(x-2)(x-3) = 24. <br>Решение. Имеем <br>х(х - 3) = х<sup>2</sup> - 3х; <br>(х - 1)(x - 2) = x<sup>2</sup>-Зx+2. | | '''Пример 5.''' Решить уравнение <br>х(х- 1)(x-2)(x-3) = 24. <br>Решение. Имеем <br>х(х - 3) = х<sup>2</sup> - 3х; <br>(х - 1)(x - 2) = x<sup>2</sup>-Зx+2. |
| Строка 91: |
Строка 97: |
| | (x<sup>2</sup> - 3x)(x<sup>2</sup> + 3x + 2) = 24 | | (x<sup>2</sup> - 3x)(x<sup>2</sup> + 3x + 2) = 24 |
| | | | |
| - | Вот теперь новая переменная «проявилась»: у = х<sup>2</sup> - Зх. <br>С ее помощью уравнение можно переписать в виде у (у + 2) = 24 и далее у<sup>2</sup> + 2у - 24 = 0. Корнями этого уравнения служат числа 4 и -6. <br>Возвращаясь к исходной переменной х , получаем два уравнения х<sup>2</sup> - Зх = 4 и х<sup>2</sup> - Зх = - 6. Из первого уравнения находим х<sub>1</sub> = 4, х<sub>2</sub> = - 1; второе уравнение не имеет корней. <br>О т в е т: 4, — 1. <br><br> | + | Вот теперь новая переменная «проявилась»: у = х<sup>2</sup> - Зх. |
| | + | |
| | + | С ее помощью уравнение можно переписать в виде у (у + 2) = 24 и далее у<sup>2</sup> + 2у - 24 = 0. Корнями этого уравнения служат числа 4 и -6. |
| | + | |
| | + | Возвращаясь к исходной переменной х , получаем два уравнения х<sup>2</sup> - Зх = 4 и х<sup>2</sup> - Зх = - 6. Из первого уравнения находим х<sub>1</sub> = 4, х<sub>2</sub> = - 1; второе уравнение не имеет корней. |
| | + | |
| | + | О т в е т: 4, — 1. <br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' | + | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' |
| | | | |
| | <br> | | <br> |
Текущая версия на 11:52, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Рациональные уравнения
Рациональные уравнения
1. Алгоритм решения рационального уравнения
Термин «рациональное уравнение» мы ввели выше в § 7. Сначала напомним, что такое рациональное выражение. Это — алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Если r(х) — рациональное выражение, то уравнение r(х) = 0 называют рациональным уравнением.
Впрочем, на практике удобнее пользоваться несколько более широким толкованием термина «рациональное уравнение»: это уравнение вида h(x) = q(x), где h(x) и q(x) — рациональные выражения.
До сих пор мы могли решить не любое рациональное уравнение, а только такое, которое в результате различных преобразований и рассуждений сводилось к линейному уравнению. Теперь наши возможности значительно больше: мы сумеем решить рациональное уравнение, которое сводится не только к линейно-
му, но и к квадратному уравнению.
Напомним, как мы решали рациональные уравнения раньше, и попробуем сформулировать алгоритм решения.
Пример 1. Решить уравнение
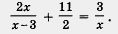
Решение. Перепишем уравнение в виде
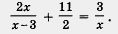 = 0 = 0
При этом, как обычно, мы пользуемся тем, что равенства А = В и А - В = 0 выражают одну и ту же зависимость между А и В. Это и позволило нам перенести член 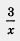 в левую часть уравнения с противоположным знаком. в левую часть уравнения с противоположным знаком.
Выполним преобразования левой части уравнения. Имеем

Вспомним условия равенства дроби нулю: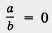 тогда, и только тогда, когда одновременно выполняются два соотношения: тогда, и только тогда, когда одновременно выполняются два соотношения:
1) числитель дроби равен нулю (а = 0); 2) знаменатель дроби отличен от нуля 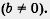 ). ).
Приравняв нулю числитель дроби в левой части уравнения (1), получим
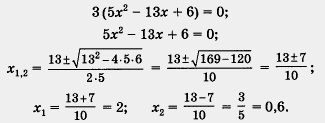
Осталось проверить выполнение второго указанного выше условия. Соотношение 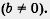 означает для уравнения (1), что означает для уравнения (1), что 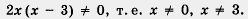 . Значения х1 = 2 и х2 = 0,6 указанным соотношениям удовлетворяют и потому служат корнями уравнения (1), а вместе с тем и корнями заданного уравнения. . Значения х1 = 2 и х2 = 0,6 указанным соотношениям удовлетворяют и потому служат корнями уравнения (1), а вместе с тем и корнями заданного уравнения.
Ответ: 2; 0,6.
Если среди корней числителя окажется число, при котором знаменатель дроби обращается в нуль, то такое число корнем уравнения быть не может, его называют посторонним корнем и в ответ не включают.
Опираясь на решенный пример, сформулируем следующий алгоритм.
Алгоритм решения рационального уравнения

Пример 2. Решить уравнение
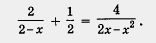
Решение. Будем действовать в соответствии с алгоритмом.
1) Преобразуем уравнение к виду
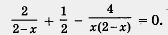
2) Выполним преобразования левой части этого уравнения:
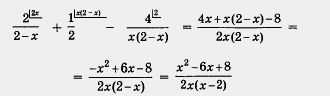
(одновременно изменили знаки в числителе и знаменателе
дроби).
Таким образом, заданное уравнение принимает вид
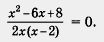
3) Решим уравнение х2 - 6x + 8 = 0. Находим
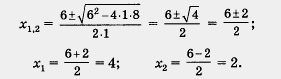
4) Для найденных значений проверим выполнение условия 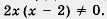 . Число 4 этому условию удовлетворяет, а число 2 — нет. Значит, 4 — корень заданного уравнения, а 2 — посторонний корень. . Число 4 этому условию удовлетворяет, а число 2 — нет. Значит, 4 — корень заданного уравнения, а 2 — посторонний корень.
О т в е т: 4.
2. Решение рациональных уравнений методом введения новой переменной
Метод введения новой переменной вам знаком, мы не раз им пользовались. Покажем на примерах, как он применяется при решении рациональных уравнений.
Пример 3. Решить уравнение х4 + х2 - 20 = 0.
Решение. Введем новую переменную у = х2. Так как х4 = (х2)2 = у2, то заданное уравнение можно переписать в виде
у2 + у - 20 = 0.
Это — квадратное уравнение, корни которого найдем, используя известные формулы; получим у1 = 4, у2 = - 5.
Но у = х2, значит, задача свелась к решению двух уравнений:
x2=4; х2=-5.
Из первого уравнения находим 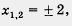 второе уравнение не имеет корней. второе уравнение не имеет корней.
Ответ: 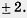 . .
Уравнение вида ах4 + bx2 +c = 0 называют биквадратным уравнением («би» — два, т. е. как бы «дважды квадратное» уравнение ). Только что решенное уравнение было именно биквадратным. Любое биквадратное уравнение решается так же, как уравнение из примера 3: вводят новую переменную у = х2, решают полученное квадратное уравнение относительно переменной у, а затем возвращаются к переменной х.
Пример 4. Решить уравнение
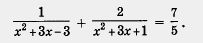
Решение. Заметим, что здесь дважды встречается одно и то же выражение х2 + Зх. Значит, имеет смысл ввести новую переменную у = х2 + Зх. Это позволит переписать уравнение в более простом и приятном виде (что, собственно говоря, и составляет цель введения новой переменной — и запись упроща
ется, и структура уравнения становится более ясной):
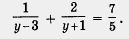
А теперь воспользуемся алгоритмом решения рационального уравнения.
1) Перенесем все члены уравнения в одну часть:
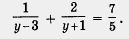 = 0 = 0
2) Преобразуем левую часть уравнения
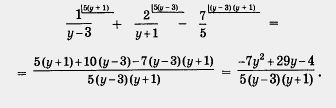
Итак, мы преобразовали заданное уравнение к виду
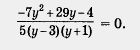
3) Из уравнения - 7у2 + 29у -4 = 0 находим 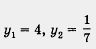 (мы с вами уже решили довольно много квадратных уравнений, так что всегда приводить в учебнике подробные выкладки, наверное, не стоит). (мы с вами уже решили довольно много квадратных уравнений, так что всегда приводить в учебнике подробные выкладки, наверное, не стоит).
4) Выполним проверку найденных корней с помощью условия 5 (у - 3) (у + 1)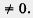 . Оба корня этому условию удовлетворяют. . Оба корня этому условию удовлетворяют.
Итак, квадратное уравнение относительно новой переменной у решено: 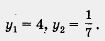
Поскольку у = х2 + Зх, а у, как мы установили, принимает два значения: 4 и 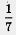 , — нам еще предстоит решить два уравнения: х2 + Зх = 4; х2 + Зх = , — нам еще предстоит решить два уравнения: х2 + Зх = 4; х2 + Зх = 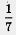 . Корнями первого уравнения являются числа 1 и - 4, корнями второго уравнения — числа . Корнями первого уравнения являются числа 1 и - 4, корнями второго уравнения — числа
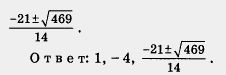
В рассмотренных примерах метод введения новой переменной был, как любят выражаться математики, адекватен ситуации, т. е. хорошо ей соответствовал. Почему? Да потому, что одно и то же выражение явно встречалось в записи уравнения несколько раз и был резон обозначить это выражение новой буквой. Но так бывает не всегда, иногда новая переменная «проявляется» только в процессе преобразований. Именно так будет обстоять дело в следующем примере.
Пример 5. Решить уравнение
х(х- 1)(x-2)(x-3) = 24.
Решение. Имеем
х(х - 3) = х2 - 3х;
(х - 1)(x - 2) = x2-Зx+2.
Значит, заданное уравнение можно переписать в виде
(x2 - 3x)(x2 + 3x + 2) = 24
Вот теперь новая переменная «проявилась»: у = х2 - Зх.
С ее помощью уравнение можно переписать в виде у (у + 2) = 24 и далее у2 + 2у - 24 = 0. Корнями этого уравнения служат числа 4 и -6.
Возвращаясь к исходной переменной х , получаем два уравнения х2 - Зх = 4 и х2 - Зх = - 6. Из первого уравнения находим х1 = 4, х2 = - 1; второе уравнение не имеет корней.
О т в е т: 4, — 1.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|