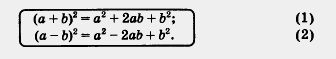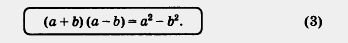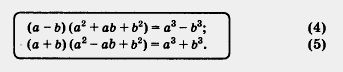Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Формулы сокращенного умножения

                           Формулы сокращенного умножения

Имеется несколько случаев, когда умножение одного многочлена на другой приводит к компактному, легко запоминающемуся результату. В этих случаях предпочтительнее не умножать каждый раз один многочлен на другой, а пользоваться готовым результатом. Рассмотрим эти случаи.

1. Квадрат суммы и квадрат разности:

Умножим двучлен а + b на себя, т.е. раскроем скобки в произведении (a + b) (а + b) или, что то же самое, в выражении (a + b)².

Имеем:

(а + b)² = (а + b) (а + b) = а • а + а • b + b • a + b • b = = а² + аЬ + аЬ + b² = а² + 2аЬ + b².

Аналогично получаем:

(a - b)² = (а-b)(а-b) = а²-аb-bа + b² = а²- 2аb + b².

Итак,

На обычном языке формулы (1) и (2) читают так: квадрат суммы (разности) двух выражений равен сумме их квадратов плюс (минус) их удвоенное произведение. Этим формулам присвоены специальные названия: формуле (1) — квадрат суммы, формуле (2) — квадрат разности.

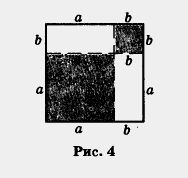
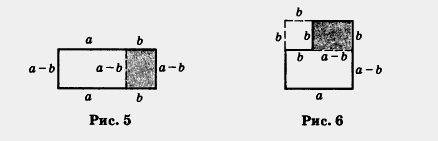
Пример 1. Раскрыть скобки в выражении:

а) (Зх + 2)²;

б) ( 5а² - 4b³)²

Решение.

а) Воспользуемся формулой (1), учтя, что в роли а выступает Зх, а в роли b — число 2.
Получим:

(Зх + 2)² = (Зх)²+ 2 • Зх • 2 + 2² = 9x² + 12x + 4.

б) Воспользуемся формулой (2), учтя, что в роли а выступает5а², а в ролиb выступает 4b³. Получим:

(5а²-4b³)²= (5а²)² - 2- 5a² • 4b³ + (4b³)²= 25a⁴-40a²b³ + 16b⁶.

При использовании формул квадрата суммы или квадрата разности учитывайте, что
(- a - b)² = (а + b)²;
( b-a )² = ( a-b )².

Это следует из того, что (- а)² = а².

Отметим, что на формулах (1) и (2) основаны некоторые математические фокусы, позволяющие производить вычисления в уме.

Например, можно практически устно возводить в квадрат числа, оканчивающиеся на 1 и 9. В самом деле

71² = (70 + 1)² = 70² + 2 • 70 • 1 + 1² = 4900 + 140 + 1 = 5041;
91² = (90 + I)²= 90² + 2 • 90 • 1 + 1² = 8100 + 180 + 1 = 8281;
69² = (70 - I)² = 70² - 2 • 70 • 1 + 1² = 4900 - 140 + 1 = 4761.

Иногда можно быстро возвести в квадрат и число, оканчивающееся цифрой 2 или цифрой 8. Например,

102² = (100 + 2)² = 100² + 2 • 100 • 2 + 2² = 10 000 + 400 + 4 = 10 404;

48² = (50 - 2)² = 50² - 2 • 50 • 2 + 2² = 2500 - 200 + 4 = 2304.

Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5.
Проведем соответствующие рассуждения для 85².

Имеем:

85² = (80 + 5)² = 80² + 2• 80 • 5 + 5² =-80 (80+ 10)+ 25 = 80 • 90 + 25 = 7200 + 25 = 7225.

Замечаем, что для вычисления 85² достаточно было умножить 8 на 9 и к полученному результату приписать справа 25. Аналогично можно поступать и в других случаях. Например, 35² = 1225  (3 • 4 = 12 и к полученному числу приписали справа 25);

65² = 4225; 1252 = 15625 (12• 18 = 156 и к полученному числу приписали справа 25).

Раз уж мы с вами заговорили о различных любопытных обстоятельствах, связанных со скучными (на первый взгляд) формулами (1) и (2), то дополним этот разговор следующим геометрическим рассуждением. Пусть а и b — положительные числа. Рассмотрим квадрат со стороной а + b и вырежем в двух его углах квадраты со сторонами, соответственно равными а и b (рис. 4).

Площадь квадрата со стороной а + b равна (а + b)². Но этот квадрат мы разрезали на четыре части: квадрат со стороной а (его площадь равна а²), квадрат со стороной b (его площадь равна b²), два прямоугольника со сторонами а и b (площадь каждого такого прямоугольника равна ab). Значит, (а + b)² = а² + b² + 2аb, т. е. получили формулу (1).

2. Разность квадратов

Умножим двучлен а + b на двучлен а - b. Получим:
(а + b) (а - b) = а² - аb + bа - b² = а² - b².
Итак

Любое равенство в математике употребляется как слева направо (т.е. левая часть равенства заменяется его правой частью), так и справа налево (т.е. правая часть равенства заменяется его левой частью). Если формулу C) использовать слева направо, то она позволяет заменить произведение (а + b) (а - b) готовым результатом а² - b². Эту же формулу можно использовать справа налево, тогда она позволяет заменить разность квадратов а² - b² произведением (а + b) (а - b). Формуле (3) в математике дано специальное название — разность квадратов.

Замечание. Не путайте термины «разность квадратов» к и «квадрат разности». Разность квадратов — это а² - b²,  значит, речь идет о формуле (3); квадрат разности — это  (a- b)², значит речь идет о формуле (2). На обычном языке формулу (3) читают «справа налево» так:

 разность квадратов двух чисел (выражений)  равна произведению суммы этих чисел (выражений) на их разность,

Пример 2. Выполнить умножение

(3x- 2y)(3x+ 2y)
Решение. Имеем:
(Зх - 2у) (Зх + 2у)= (Зx)² - (2у)² = 9x² - 4y².

Пример 3. Представить двучлен 16x⁴ - 9 в виде произведения двучленов.

Решение. Имеем: 16x⁴ =(4x²)², 9 = З², значит, заданный двучлен есть разность квадратов, т.е. к нему можно применить формулу (3), прочитанную справа налево. Тогда получим:

16x⁴ - 9 = (4x²)²- З² = (4x² + 3)(4x² - 3)

Формула (3), как и формулы (1) и (2), используется для математических фокусов. Смотрите:

79 • 81 = (80 - 1) (80 + 1) - 802 - I2 = 6400 - 1 = 6399;
42 • 38 = D0 + 2) D0 - 2) = 402 - 22 = 1600 - 4 = 1596.

Завершим разговор о формуле разности квадратов любопытным геометрическим рассуждением. Пусть а и b — положительные числа, причем а > b. Рассмотрим прямоугольник со сторонами а + b и а - b (рис. 5). Его площадь равна (а + b) (а - b). Отрежем прямоугольник со сторонами b и а - b и подклеим его к оставшейся части так, как показано на рисунке 6. Ясно, что полученная фигура имеет ту же площадь, т. е. (а + b) (а - b). Но эту фигуру можно
построить так: из квадрата со стороной а вырезать квадрат со стороной b (это хорошо видно на рис. 6). Значит, площадь новой фигуры равна а² - b². Итак, (а + b) (а - b) = а² - b², т. е. получили формулу (3).

3. Разность кубов и сумма кубов

Умножим двучлен а - b на трехчлен а² + ab + b².
Получим:
(a - b) (а² + ab + b²) = а • а² + а • ab + а • b² - b • а² - b • аb -b•b² = а³ + а²b + аb²-а²b-аb²-b³ = а³-b³.

Аналогично

(а + b) (а² - аb + b²) = а³ + b³

(проверьте это сами). Итак,

Формулу (4) обычно называют разностью кубов, формулу( 5) — суммой кубов. Попробуем перевести формулы (4) и (5) на обычный язык. Прежде чем это сделать, заметим, что выражение a² + ab + b² похоже на выражение а² + 2ab + b², которое фигурировало в формуле (1) и давало (а + b)²; выражение а² - ab + b² похоже на выражение а² - 2ab + b², которое фигурировало в формуле (2) и давало (а - b)².

Чтобы отличить (в языке) эти пары выражений друг от друга, каждое из выражений а² + 2ab + b² и а² - 2ab + b² называют полным квадратом (суммы или разности), а каждое из выражений а² + ab + b² и а² - ab + b² называют неполным квадратом (суммы или разности). Тогда получается следующий перевод формул (4) и (5) (прочитанных «справа налево») на обычный язык:

разность кубов двух чисел (выражений) равна произведению разности этих чисел (выражений) на неполный квадрат их суммы; сумма кубов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на неполный квадрат их разности.

Замечание. Все полученные в этом параграфе формулы (1)-(5) используются как слева направо, так и справа налево, только в первом случае (слева направо) говорят, что (1 )-(5) — формулы сокращенного умножения, а во втором случае (справа налево) говорят, что (1)-(5) — формулы разложения на множители.

Пример 4. Выполнить умножение (2х- 1)(4x² + 2х +1).

Решение. Так как первый множитель есть разность одночленов 2х и 1, а второй множитель — неполный квадрат их суммы, то можно воспользоваться формулой (4). Получим:

(2х - 1)( 4x² + 2х + 1) = (2x)³ - I³ = 8x³ - 1.

Пример 5. Представить двучлен 27а⁶ + 8b³ в виде произведения многочленов.

Решение. Имеем: 27а⁶ = (За²)³, 8b³ =(2b)³. Значит, заданный двучлен есть сумма кубов, т. е. к нему можно применить формулу 95), прочитанную справа налево. Тогда получим:

27а⁶ + 8b³ = (За²)³ + (2b)³ = (За² + 2Ь) ((За²)² - За² • 2Ь + (2b)²) = (За² + 2Ь) (9а⁴ - 6а²Ь + 4b²).

_{Помощь школьнику онлайн, Математика для 7 класса скачать, календарно-тематическое планирование}

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.