|
|
|
| (6 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Приближенные значения действительных чисел</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Приближенные значения действительных чисел, уравнения, координатами, десятичными дробями, числа, цифра, координатной прямой</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Приближенные значения действительных чисел''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Приближенные значения действительных чисел'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| - | <br> | + | '''Приближенные значения действительных чисел'''<br><br>И в 7-м и в 8-м классе мы часто решали уравнения графически. Заметили ли вы, что практически во всех таких примерах '''[[Розв'язування рівнянь. Презентація уроку|уравнения]]''' имели «хорошие» корни? Это были целые числа, которые без труда отыскивались с помощью графиков, особенно на клетчатой бумаге. Но так бывает далеко не всегда, просто мы до сих пор подбирали «хорошие» примеры. |
| | | | |
| - | ''' ПРИБЛИЖЕННЫЕ ЗНАЧЕНИЯ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ '''<br><br>И в 7-м и в 8-м классе мы часто решали уравнения графически. Заметили ли вы, что практически во всех таких примерах уравнения имели «хорошие» корни? Это были целые числа, которые без труда отыскивались с помощью графиков, особенно на клетчатой бумаге. Но так бывает далеко не всегда, просто мы до сих пор подбирали «хорошие» примеры. | + | Рассмотрим два уравнения: [[Image:14-06-154.jpg]] = 2 - х и [[Image:14-06-154.jpg]] = 4 - х. Первое уравнение имеет единственный корень х = 1, поскольку графики функций у =[[Image:14-06-154.jpg]] и у = 2 - х пересекаются в одной точке А (1; 1) (рис. 112). Во втором случае графики функций [[Image:14-06-154.jpg]]— фс и у = 4 - х также пересекаются в одной точке В (рис. 113), но с «плохими» '''[[Координатная прямая|координатами]]'''. Пользуясь чертежом, можно сделать вывод, что абсцисса точки В примерно равна 2,5. В подобных случаях говорят не о точном, а о приближенном решении уравнения и пишут так:[[Image:14-06-155.jpg]]<br> |
| | | | |
| - | Рассмотрим два уравнения: [[Image:14-06-154.jpg]] = 2 - х и [[Image:14-06-154.jpg]] = 4 - х. Первое уравнение имеет единственный корень х = 1, поскольку графики функций у =[[Image:14-06-154.jpg]] и у = 2 - х пересекаются в одной точке А (1; 1) (рис. 112). Во втором случае графики функций [[Image:14-06-154.jpg]]— фс и у = 4 - х также пересекаются в одной точке В (рис. 113), но с «плохими» координатами. Пользуясь чертежом, можно сделать вывод, что абсцисса точки В примерно равна 2,5. В подобных случаях говорят не о точном, а о приближенном решении уравнения и пишут так:[[Image:14-06-155.jpg]]<br>
| + | [[Image:14-06-156.jpg|480px|Графики]]<br>Это одна из причин, по которым математики решили ввести понятие приближенного значения действительного числа. Есть и вторая причина, причем, может быть, даже более важная.Что такое действительное число? Это бесконечная десятичная дробь. Но производить вычисления с бесконечными '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичными дробями]]''' неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Например, для числа [[Image:14-06-157.jpg]] пользуются приближенным равенством [[Image:14-06-158.jpg]]3,141 или [[Image:14-06-158.jpg]] 3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Можно взять более точные приближения: например, [[Image:14-06-158.jpg]]3,1415 — приближение по недостатку с точностью до 0,0001;[[Image:14-06-158.jpg]] 3,1416 — приближение по избытку с точностью до 0,0001. Можно взять менее точные приближения, скажем, с точностью до 0,01: по недостатку [[Image:14-06-158.jpg]] 3,14, по избытку [[Image:14-06-158.jpg]] 3,15. |
| | | | |
| - | <br>
| + | Знак приближенного равенства » вы использовали и в курсе математики 5—6-го классов и, вероятно, в курсе физики, да и мы пользовались им раньше, например в § 27. |
| | | | |
| - | [[Image:14-06-156.jpg]]<br>
| + | '''Пример 1.''' Найти приближенные значения по недостатку и по избытку с точностью до 0,01 для чисел: |
| | | | |
| - | <br>Это одна из причин, по которым математики решили ввести понятие приближенного значения действительного числа. Есть и вторая причина, причем, может быть, даже более важная.Что такое действительное число? Это бесконечная десятичная дробь. Но производить вычисления с бесконечными десятичными дробями неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Например, для числа [[Image:14-06-157.jpg]] пользуются приближенным равенством [[Image:14-06-158.jpg]]3,141 или [[Image:14-06-158.jpg]] 3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Можно взять более точные приближения: например, <br>[[Image:14-06-158.jpg]]3,1415 — приближение по недостатку с точностью до 0,0001;[[Image:14-06-158.jpg]] 3,1416 — приближение по избытку с точностью до 0,0001. Можно взять менее точные приближения, скажем, с точностью до 0,01: по недостатку [[Image:14-06-158.jpg]] 3,14, по избытку [[Image:14-06-158.jpg]] 3,15. <br>Знак приближенного равенства » вы использовали и в курсе математики 5—6-го классов и, вероятно, в курсе физики, да и мы пользовались им раньше, например в § 27.
| + | [[Image:14-06-159.jpg|180px|Пример]] |
| | | | |
| - | '''Пример 1.''' Найти приближенные значения по недостатку и по избытку с точностью до 0,01 для чисел: <br>[[Image:14-06-159.jpg]]<br>Решение,
| + | Решение, |
| | | | |
| - | а) Мы знаем, что [[Image:14-06-160.jpg]] = 2,236... (см. § 27), следовательно, [[Image:14-06-160.jpg]] [[Image:14-06-163.jpg]] 2,23 — это приближение по недостатку с точностью до 0,01; [[Image:14-06-160.jpg]] [[Image:14-06-163.jpg]] 2,24 — это приближение по избытку с точностью до 0,01. <br>б) 2 +[[Image:14-06-160.jpg]] = 2,000... + 2,236... = 4,236... . Значит, 2 + [[Image:14-06-160.jpg]][[Image:14-06-163.jpg]] 4,23 — это приближение по недостатку с точностью до 0,01; 2 + [[Image:14-06-160.jpg]] 4,24 — это приближение по избытку с точностью до 0,01. <br>в) Имеем [[Image:14-06-164.jpg]][[Image:14-06-162.jpg]] [[Image:14-06-163.jpg]] 0,31818... (см. § 26). Таким образом, [[Image:14-06-162.jpg]] [[Image:14-06-164.jpg]][[Image:14-06-163.jpg]] 0,31 — это приближение по недостатку с точностью до 0,01; <br>7 <br>— » 0,32 — это приближение по избытку с точностью до 0,01. (И <br>Приближение по недостатку и приближение по избытку <br>называют иногда округлением числа. <br>Определение. Погрешностью приближе- <br>ния (абсолютной погрешностью) называют мо- <br>дуль разности между точным значением величи- <br>ны х и ее приближенным значением а: погреш- <br>абсолютная ность приближения — это | х - а |. <br>погрешность <br>Например, погрешность приближенного ра- <br>венства п « 3,141 или п а 3,142 выражается как \п - 3, 1411 или <br>соответственно как \п - 3, 142 [. <br>Возникает чисто практический вопрос: какое приближение <br>лучше, по недостатку или по избытку, т. е. в каком случае <br>погрешность меньше? Это, конечно, зависит от конкретного чи- <br>сла, для которого составляются приближения. Обычно при <br>округлении положительных чисел пользуются следующим пра- <br>вилом: <br>Правило округления. Если первая отбра- <br>сываемая цифра меньше 5, то нужно брать <br>приближение по недостатку; если первая от- <br>брасываемая цифра больше или равна 5, то <br>нужно брать приближение по избытку. <br>Применим это правило ко всем рассмотренным в этом пара- <br>графе числам; выберем для рассмотренных чисел те приближе- <br>ния, для которых погрешность окажется наименьшей. <br>1) п = 3,141592... . С точностью до 0,001 имеем п « 3,142; <br>здесь первая отбрасываемая цифра равна 5 (на четвертом месте <br>после запятой), поэтому взяли приближение по избытку. <br>С точностью до 0,0001 имеем п а 3,1416 — и здесь взяли прибли- <br>жение по избытку, поскольку первая отбрасываемая цифра (на <br>пятом месте после запятой) равна 9. А вот срочностью до 0,01 <br>надо взять приближение по недостатку: п « 3,14. <br>2) JE = 2,236... . С точностью до 0,01 имеем JE * 2,24 <br>(приближение по избытку). ¦ <br>3) 2 + J& = 4,236... . С точностью до 0,01 имеем 2 + ,/5 « <br>«4,24 (приближение по избытку). <br>7 7 <br>4) — = 0,31818... . С точностью до 0,001 имеем — « 0,318 <br>2i2i <br>(приближение по недостатку). <br>Рассмотрим последний пример <br>подробнее. Возьмем укрупненный <br>фрагмент координатной прямой <br>7 <br>(рис. 114). Точка — принадлежит <br>2i2i <br>отрезку [0,318, 0,319], значит, ее расстояния от концов отрезка <br>7 <br>не превосходят длины отрезка. Расстояния точки — от концов <br>22 <br>0*^9 <br>рис <br>отрезка равны соответственно <br>22 <br>¦к ~ °'319 <br>отрезка [0,318, 0,319] равна 0,001. Значит, <br>Тг - °'318 <br>, а длина <br>0,001 <br>i - °>319 <br>0,001. <br>Итак, в обоих случаях (и для приближения числа — по не- <br>LiCi <br>достатку, и для приближения его по избытку) погрешность не <br>превосходит 0,001. <br>До сих пор мы говорили: приближения с точностью до 0,01, <br>до 0,001 и т. д. Теперь мы можем навести порядок в использо- <br>вании терминологии. <br>Если а — приближенное значение числа х и \ х — а\ < h, mo <br>говорят, что погрешность приближения не превосходит h <br>или что число х равно числу а с точностью до h. <br>Почему же важно уметь находить прибли- <br>женные значения чисел? Дело в том, что прак- <br>тически невозможно оперировать с бесконеч- <br>ными десятичными дробями и использовать их <br>для измерения величин. На практике во многих <br>случаях вместо точных значений берут приближения с заранее <br>заданной точностью (погрешностью). Эта идея заложена и в <br>калькуляторах, на дисплеях которых высвечивается конечная <br>десятичная дробь, т. е. приближение выводимого на экран числа <br>(за редким исключением, когда выводимое число представляет <br>собой конечную десятичную дробь, умещающуюся на экране). <br><br><br><br><br><br> | + | а) Мы знаем, что [[Image:14-06-160.jpg]] = 2,236... (см. § 27), следовательно, [[Image:14-06-160.jpg]] [[Image:14-06-163.jpg]] 2,23 — это приближение по недостатку с точностью до 0,01; [[Image:14-06-160.jpg]] [[Image:14-06-163.jpg]] 2,24 — это приближение по избытку с точностью до 0,01. <br>б) 2 +[[Image:14-06-160.jpg]] = 2,000... + 2,236... = 4,236... . Значит, 2 + [[Image:14-06-160.jpg]][[Image:14-06-163.jpg]] 4,23 — это приближение по недостатку с точностью до 0,01; 2 + [[Image:14-06-160.jpg]][[Image:14-06-163.jpg]] 4,24 — это приближение по избытку с точностью до 0,01. <br>в) Имеем [[Image:14-06-164.jpg]] [[Image:14-06-163.jpg]] 0,31818... (см. § 26). Таким образом, [[Image:14-06-164.jpg]] [[Image:14-06-163.jpg]] 0,31 — это приближение по недостатку с точностью до 0,01; [[Image:14-06-164.jpg]] [[Image:14-06-163.jpg]] 0,32 — это приближение по избытку с точностью до 0,01. <br>Приближение по недостатку и приближение по избытку называют иногда округлением '''[[Обозначение натуральных чисел|натуральные числа]]'''. |
| | | | |
| - | <br> | + | '''''Определение.'''''Погрешностью приближения (абсолютной погрешностью) называют модуль разности между точным значением величины х и ее приближенным значением а: погрешность приближения — это | х - а |. <br>Например, погрешность приближенного равенства [[Image:14-06-165.jpg]] выражается как [[Image:14-06-166.jpg]] или соответственно как [[Image:14-06-167.jpg]],<br>Возникает чисто практический вопрос: какое приближение лучше, по недостатку или по избытку, т. е. в каком случае погрешность меньше? Это, конечно, зависит от конкретного числа, для которого составляются приближения. Обычно при округлении положительных чисел пользуются следующим правилом: |
| | | | |
| - | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | [[Image:14-06-168.jpg|480px|Правило округления]]<br><br>Применим это правило ко всем рассмотренным в этом параграфе числам; выберем для рассмотренных чисел те приближения, для которых погрешность окажется наименьшей. |
| | + | |
| | + | 1) [[Image:14-06-169.jpg]] = 3,141592... . С точностью до 0,001 имеем [[Image:14-06-158.jpg]]3,142; здесь первая отбрасываемая '''[[Ілюстрації: Лічба предметів. Порівняння предметів за величиною. Підготовчі вправи до написання цифр.|цифра]]''' равна 5 (на четвертом месте после запятой), поэтому взяли приближение по избытку. |
| | + | |
| | + | С точностью до 0,0001 имеем [[Image:14-06-158.jpg]] 3,1416 — и здесь взяли приближение по избытку, поскольку первая отбрасываемая цифра (на пятом месте после запятой) равна 9. А вот с точностью до 0,01 надо взять приближение по недостатку: [[Image:14-06-158.jpg]] 3,14. |
| | + | |
| | + | 2)[[Image:14-06-160.jpg]] = 2,236... . С точностью до 0,01 имеем [[Image:14-06-160.jpg]] [[Image:14-06-163.jpg]] 2,24 (приближение по избытку).<br>3) 2 + [[Image:14-06-160.jpg]] = 4,236... . С точностью до 0,01 имеем 2 + [[Image:14-06-160.jpg]] [[Image:14-06-163.jpg]]4,24 (приближение по избытку). <br>4) [[Image:14-06-162.jpg]] = 0,31818... . С точностью до 0,001 имеем [[Image:14-06-162.jpg]] [[Image:14-06-163.jpg]] 0,318 (приближение по недостатку). <br>Рассмотрим последний пример подробнее. Возьмем укрупненный фрагмент '''[[Порівняння натуральних чисел за допомогою координатного променя. Презентація уроку|координатной прямой]]''' (рис. 114). |
| | + | |
| | + | [[Image:14-06-170.jpg|240px|Пример]]<br> |
| | + | |
| | + | Точка [[Image:14-06-162.jpg]] принадлежит отрезку [0,318, 0,319], значит, ее расстояния от концов отрезка не превосходят длины отрезка. Расстояния точки [[Image:14-06-162.jpg]] от концов отрезка равны соответственно [[Image:14-06-171.jpg|180px|Решение]] отрезка [0,318, 0,319] равна 0,001. Значит, [[Image:14-06-173.jpg|140px|Решение]] и [[Image:14-06-174.jpg|160px|Решение]]<br>Итак, в обоих случаях (и для приближения числа [[Image:14-06-162.jpg]] по недостатку, и для приближения его по избытку) погрешность не превосходит 0,001. |
| | + | |
| | + | До сих пор мы говорили: приближения с точностью до 0,01, до 0,001 и т. д. Теперь мы можем навести порядок в использовании терминологии. |
| | + | |
| | + | Если а — приближенное значение числа х и [[Image:14-06-175.jpg|80px|Задание]], тo говорят, что погрешность приближения не превосходит h или что число х равно числу а с точностью до h. |
| | + | |
| | + | Почему же важно уметь находить приближенные значения чисел? Дело в том, что практически невозможно оперировать с бесконечными десятичными дробями и использовать их для измерения величин. На практике во многих случаях вместо точных значений берут приближения с заранее заданной точностью (погрешностью). Эта идея заложена и в калькуляторах, на дисплеях которых высвечивается конечная десятичная дробь, т. е. приближение выводимого на экран числа (за редким исключением, когда выводимое число представляет собой конечную десятичную дробь, умещающуюся на [http://xvatit.com/it '''экране''']). <br><br> |
| | + | |
| | + | ''Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' |
| | | | |
| | <br> | | <br> |
| | + | |
| | + | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub><br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 15:58, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Приближенные значения действительных чисел
Приближенные значения действительных чисел
И в 7-м и в 8-м классе мы часто решали уравнения графически. Заметили ли вы, что практически во всех таких примерах уравнения имели «хорошие» корни? Это были целые числа, которые без труда отыскивались с помощью графиков, особенно на клетчатой бумаге. Но так бывает далеко не всегда, просто мы до сих пор подбирали «хорошие» примеры.
Рассмотрим два уравнения: 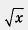 = 2 - х и = 2 - х и 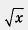 = 4 - х. Первое уравнение имеет единственный корень х = 1, поскольку графики функций у = = 4 - х. Первое уравнение имеет единственный корень х = 1, поскольку графики функций у =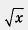 и у = 2 - х пересекаются в одной точке А (1; 1) (рис. 112). Во втором случае графики функций и у = 2 - х пересекаются в одной точке А (1; 1) (рис. 112). Во втором случае графики функций 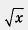 — фс и у = 4 - х также пересекаются в одной точке В (рис. 113), но с «плохими» координатами. Пользуясь чертежом, можно сделать вывод, что абсцисса точки В примерно равна 2,5. В подобных случаях говорят не о точном, а о приближенном решении уравнения и пишут так: — фс и у = 4 - х также пересекаются в одной точке В (рис. 113), но с «плохими» координатами. Пользуясь чертежом, можно сделать вывод, что абсцисса точки В примерно равна 2,5. В подобных случаях говорят не о точном, а о приближенном решении уравнения и пишут так: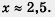
Это одна из причин, по которым математики решили ввести понятие приближенного значения действительного числа. Есть и вторая причина, причем, может быть, даже более важная.Что такое действительное число? Это бесконечная десятичная дробь. Но производить вычисления с бесконечными десятичными дробями неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Например, для числа  пользуются приближенным равенством пользуются приближенным равенством  3,141 или 3,141 или 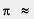 3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Можно взять более точные приближения: например, 3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Можно взять более точные приближения: например, 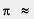 3,1415 — приближение по недостатку с точностью до 0,0001; 3,1415 — приближение по недостатку с точностью до 0,0001;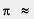 3,1416 — приближение по избытку с точностью до 0,0001. Можно взять менее точные приближения, скажем, с точностью до 0,01: по недостатку 3,1416 — приближение по избытку с точностью до 0,0001. Можно взять менее точные приближения, скажем, с точностью до 0,01: по недостатку 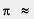 3,14, по избытку 3,14, по избытку 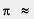 3,15. 3,15.
Знак приближенного равенства » вы использовали и в курсе математики 5—6-го классов и, вероятно, в курсе физики, да и мы пользовались им раньше, например в § 27.
Пример 1. Найти приближенные значения по недостатку и по избытку с точностью до 0,01 для чисел:
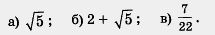
Решение,
а) Мы знаем, что 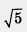 = 2,236... (см. § 27), следовательно, = 2,236... (см. § 27), следовательно, 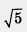 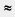 2,23 — это приближение по недостатку с точностью до 0,01; 2,23 — это приближение по недостатку с точностью до 0,01; 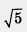 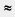 2,24 — это приближение по избытку с точностью до 0,01. 2,24 — это приближение по избытку с точностью до 0,01.
б) 2 +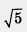 = 2,000... + 2,236... = 4,236... . Значит, 2 + = 2,000... + 2,236... = 4,236... . Значит, 2 + 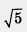  4,23 — это приближение по недостатку с точностью до 0,01; 2 + 4,23 — это приближение по недостатку с точностью до 0,01; 2 + 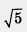  4,24 — это приближение по избытку с точностью до 0,01. 4,24 — это приближение по избытку с точностью до 0,01.
в) Имеем 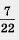  0,31818... (см. § 26). Таким образом, 0,31818... (см. § 26). Таким образом, 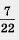  0,31 — это приближение по недостатку с точностью до 0,01; 0,31 — это приближение по недостатку с точностью до 0,01; 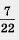  0,32 — это приближение по избытку с точностью до 0,01. 0,32 — это приближение по избытку с точностью до 0,01.
Приближение по недостатку и приближение по избытку называют иногда округлением натуральные числа.
Определение.Погрешностью приближения (абсолютной погрешностью) называют модуль разности между точным значением величины х и ее приближенным значением а: погрешность приближения — это | х - а |.
Например, погрешность приближенного равенства 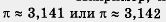 выражается как выражается как 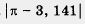 или соответственно как или соответственно как 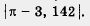 , ,
Возникает чисто практический вопрос: какое приближение лучше, по недостатку или по избытку, т. е. в каком случае погрешность меньше? Это, конечно, зависит от конкретного числа, для которого составляются приближения. Обычно при округлении положительных чисел пользуются следующим правилом:

Применим это правило ко всем рассмотренным в этом параграфе числам; выберем для рассмотренных чисел те приближения, для которых погрешность окажется наименьшей.
1) 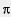 = 3,141592... . С точностью до 0,001 имеем = 3,141592... . С точностью до 0,001 имеем 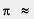 3,142; здесь первая отбрасываемая цифра равна 5 (на четвертом месте после запятой), поэтому взяли приближение по избытку. 3,142; здесь первая отбрасываемая цифра равна 5 (на четвертом месте после запятой), поэтому взяли приближение по избытку.
С точностью до 0,0001 имеем 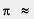 3,1416 — и здесь взяли приближение по избытку, поскольку первая отбрасываемая цифра (на пятом месте после запятой) равна 9. А вот с точностью до 0,01 надо взять приближение по недостатку: 3,1416 — и здесь взяли приближение по избытку, поскольку первая отбрасываемая цифра (на пятом месте после запятой) равна 9. А вот с точностью до 0,01 надо взять приближение по недостатку: 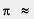 3,14. 3,14.
2)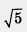 = 2,236... . С точностью до 0,01 имеем = 2,236... . С точностью до 0,01 имеем 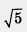  2,24 (приближение по избытку). 2,24 (приближение по избытку).
3) 2 + 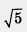 = 4,236... . С точностью до 0,01 имеем 2 + = 4,236... . С точностью до 0,01 имеем 2 + 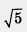 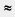 4,24 (приближение по избытку). 4,24 (приближение по избытку).
4) 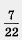 = 0,31818... . С точностью до 0,001 имеем = 0,31818... . С точностью до 0,001 имеем 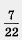  0,318 (приближение по недостатку). 0,318 (приближение по недостатку).
Рассмотрим последний пример подробнее. Возьмем укрупненный фрагмент координатной прямой (рис. 114).
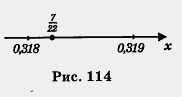
Точка 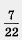 принадлежит отрезку [0,318, 0,319], значит, ее расстояния от концов отрезка не превосходят длины отрезка. Расстояния точки принадлежит отрезку [0,318, 0,319], значит, ее расстояния от концов отрезка не превосходят длины отрезка. Расстояния точки 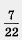 от концов отрезка равны соответственно от концов отрезка равны соответственно 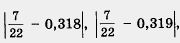 отрезка [0,318, 0,319] равна 0,001. Значит, отрезка [0,318, 0,319] равна 0,001. Значит, 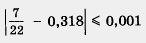 и и 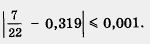
Итак, в обоих случаях (и для приближения числа 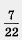 по недостатку, и для приближения его по избытку) погрешность не превосходит 0,001. по недостатку, и для приближения его по избытку) погрешность не превосходит 0,001.
До сих пор мы говорили: приближения с точностью до 0,01, до 0,001 и т. д. Теперь мы можем навести порядок в использовании терминологии.
Если а — приближенное значение числа х и 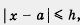 , тo говорят, что погрешность приближения не превосходит h или что число х равно числу а с точностью до h. , тo говорят, что погрешность приближения не превосходит h или что число х равно числу а с точностью до h.
Почему же важно уметь находить приближенные значения чисел? Дело в том, что практически невозможно оперировать с бесконечными десятичными дробями и использовать их для измерения величин. На практике во многих случаях вместо точных значений берут приближения с заранее заданной точностью (погрешностью). Эта идея заложена и в калькуляторах, на дисплеях которых высвечивается конечная десятичная дробь, т. е. приближение выводимого на экран числа (за редким исключением, когда выводимое число представляет собой конечную десятичную дробь, умещающуюся на экране).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













