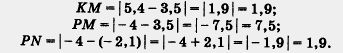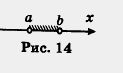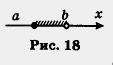|
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Координатная прямая
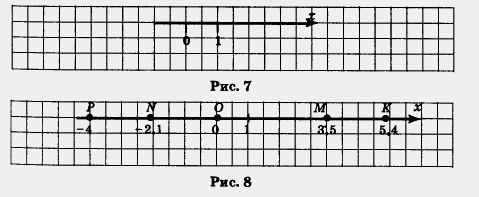
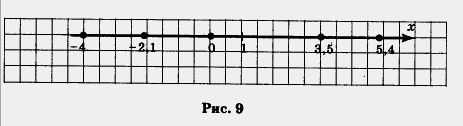
Начиная с главы 6 мы будем изучать не только новые аналитические, но и графические (геометрические) модели. Они строятся с помощью координатной прямой, координатной плоскости. Эти понятия вам немного знакомы из курса математики 5-6 классов. Прямую /, на которой выбрана начальная точка О (начало отсчета), масштаб (единичный отрезок, т. е. отрезок, длина которого считается равной 1) и положительное направление, называют координатной прямой, или координатной осью (рис. 7); употребляют также термин «ось х". Каждому числу соответствует единственная точка прямой. Например, числу 3,5 соответствует точка М (рис. 8), которая удалена от начала отсчета, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении. Числу -4 соответствует точка Р (см. рис. 8), которая удалена от точки О на расстояние, равное 4, и отложена от точки О в отрицательном направлении, т. е. в направлении, противоположном заданному. Верно и обратное: каждая точка координатной прямой соответствует единственному числу. Например, точка К, удаленная от точки О на расстояние 5,4 в положительном (заданном) направлении, соответствует числу 5,4, а точка N, удаленная от точки О на расстояние 2,1 в отрицательном направлении, соответствует числу - 2,1 (см. рис. 8). Указанные числа называют координатами соответствующих точек. Так, на рис. 8 точка К имеет координату 5,4; точка Р — координату -4; точка М — координату 3,5; точка N — координату -2,1; точка О — координату 0 (нуль). Отсюда и происходит название — «координатная прямая». Образно выражаясь, координатная прямая — это густо заселенный дом, жильцы этого дома — точки, а координаты точек — это номера квартир, в которых живут точки- жильцы.
Координатная прямая дает нам возможность свободно переходить с алгебраического языка на геометрический и обратно. Пусть, например, число а меньше числа Ь. На алгебраическом языке это записывается так: а < b; на геометрическом языке это означает, что точка а расположена на координатной прямой левее точки b. Познакомимся еще с несколькими элементами математического языка, которые связаны с координатной прямой.
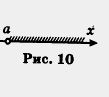
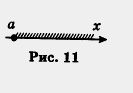
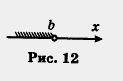
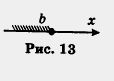
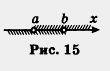
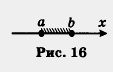
Обратите внимание: точка а открытому лучу не принадлежит, а eсли же эту точку надо присоединить к открытому лучу, то пишут х > a или [a, + оо) ( перед а ставят не круглую, а квадратную скобку), а на чертеже такую точку обозначают не светлым, как на рис. 10, а закрашенным кружком (рис. 11). Если про множество точек (а, +oо) говорят, что это — открытый луч, то для [a, + оо) употребляют термин луч (без прилагательного «открытый»). 2. Пусть на координатной прямой отмечена точка b. Рассмотрим все точки, которые лежат на прямой левее точки b, и отметим соответствующую часть координатной прямой штриховкой (рис. 12). Это множество точек (чисел) также называют открытым лучом и обозначают (-оо, b), где знак — оо читается: «минус бесконечность». для (- оо, b) также будем употреблять термин луч. 3. Пусть на координатной прямой отмечены точки а и b, причем а < b (т. е. точка а расположена на прямой левее точки b). Рассмотрим все точки, которые лежат правее точки а, но левее точки b отметим соответствующую часть координатной прямой штриховкой (рис. 14). Это множество (чисел) называют интервалом и обозначают (а, b). Оно характеризуется строгим двойным неравенством a < х < b (под х понимается любая точка интервала). Обратите внимание: интервал (а, b) есть пересечение (общая часть) двух открытых лучей (-оо, b) и (а, + оо) — это хорошо видно на рисунке 15.
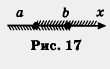
который характеризуется нестрогим двойным неравенством а < х < b. Обратите внимание: в обозначении отрезка используют не круглые скобки, как это было в обозначении интервала, а квадратные; на чертеже точки а и b отмечены темными кружками, а не светлыми, как это было в случае интервала. Отрезок [а, b] есть пересечение (общая часть) двух лучей (-оо, b] и [a, +оо) — это хорошо видно на рисунке 17.
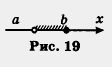
или только точку b (рис. 19)? Получится полуинтервал, который в первом случае обозначают [a, b), а во втором — (а, b] и который характеризуется с помощью двойных неравенств: a < х < b — в первом случае, a < х < b — во втором случае. Итак, мы ввели пять новых терминов математического языка: луч, открытый луч, интервал, отрезок, полуинтервал. Есть и общий термин: числовые промежутки. Сама координатная прямая также считается числовым промежутком; для нее используют обозначение (-оо, +оо).
Математика за 7 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: