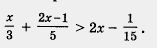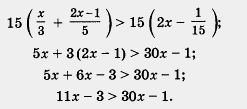|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Решение линейных неравенств</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Решение линейных неравенств, уравнения, число, отрицательное число, знаменателей</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Решение линейных неравенств''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Решение линейных неравенств''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | '''Решение линейных неравенств'''<br> |
| | | | |
| | + | <br>Свойства числовых равенств помогали нам решать '''[[Розв'язування рівнянь. Презентація уроку|уравнения]]''', т. е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств помогут нам решать неравенства с переменной, т. е. находить те значения переменной, при которых неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной. |
| | | | |
| - | ''' РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ '''<br>
| + | Рассмотрим, например, неравенство 2х + 5 < 7. <br> |
| | | | |
| - | <br>Свойства числовых равенств помогали нам решать уравнения, т. е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств помогут нам решать неравенства с переменной, т. е. находить те значения переменной, при которых <br>неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной.
| + | Подставив вместо х значение 0, получим 5 < 7 — верное неравенство; значит, х = 0 — решение данного неравенства. |
| | | | |
| - | Рассмотрим, например, неравенство 2х + 5 < 7. <br>Подставив вместо х значение 0, получим 5 < 7 — верное неравенство; значит, х = 0 — решение данного неравенства.
| + | Подставив вместо х значение 1, получим 7 < 7 — неверное '''[[Презентація до теми Розв'язування лінійних нерівностей|неравенство]]'''; поэтому х = 1 не является решением данного неравенства. Подставив вместо х значение -3, получим -6 + 5 < 7, т.е. -1 < 7 — верное неравенство; следовательно, х = -3 — решение данного неравенства. Подставив вместо х значение 2,5, получим 2-2,5 + 5 < 7, т.е. 10 < 7 — неверное неравенство. |
| | | | |
| - | Подставив вместо х значение 1, получим 7 < 7 — неверное неравенство; поэтому х = 1 не является решением данного неравенства. Подставив вместо х значение -3, получим -6 + 5 < 7, т.е. -1 < 7 — верное неравенство; следовательно, х = -3 — решение данного неравенства. Подставив вместо х значение 2,5, <br>получим 2-2,5 + 5 < 7, т.е. 10 < 7 — неверное неравенство.
| + | Значит, х = 2,5 не является решением неравенства. <br> |
| | | | |
| - | Значит, х = 2,5 не является решением неравенства. <br>
| + | Но вы же понимаете, что это — тупиковый путь: ни один математик не станет так решать неравенство, ведь все числа невозможно перебрать! Вот тут-то и нужно использовать свойства числовых неравенств, рассуждая следующим образом. <br> |
| | | | |
| - | Но вы же понимаете, что это — тупиковый путь: ни один математик не станет так решать неравенство, ведь все числа невозможно перебрать! Вот тут-то и нужно использовать свойства числовых неравенств, рассуждая следующим образом. <br>
| + | Нас интересуют такие числа х, при которых 2х + 5 < 7 — верное числовое неравенство. Но тогда и 2х + 5-5<7-5 — верное неравенство (согласно свойству 2: к обеим частям неравенства прибавили одно и то же '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|число]]''' - 5). <br> |
| | | | |
| - | Нас интересуют такие числа х, при которых 2х + 5 < 7 — верное числовое неравенство. Но тогда и 2х + 5-5<7-5 — верное неравенство (согласно свойству 2: к обеим частям неравенства прибавили одно и то же число - 5). Получили более простое неравенство 2х < 2. Разделив обе его части на положительное число 2, получим (на основании свойства 3) верное неравенство х < 1. <br>
| + | Получили более простое неравенство 2х < 2. Разделив обе его части на положительное число 2, получим (на основании свойства 3) верное неравенство х < 1. <br> |
| | | | |
| - | Что это значит? Это значит, что решением неравенства является любое число х, которое меньше 1. Эти числа заполняют открытый луч (-oо, 1). . Обычно говорят, что этот луч — решение неравенства 2х + 5 < 7 (точнее было бы говорить о множестве решений, но математики, как всегда, экономны в словах).<br> | + | Что это значит? Это значит, что решением неравенства является любое число х, которое меньше 1. Эти числа заполняют открытый луч (-oо, 1). . Обычно говорят, что этот луч — решение неравенства 2х + 5 < 7 (точнее было бы говорить о множестве решений, но математики, как всегда, экономны в словах).<br> |
| | | | |
| - | Таким образом, можно использовать два варианта записи решений данного неравенства: х < 1 или (-oо, 1). <br> | + | Таким образом, можно использовать два варианта записи решений данного неравенства: х < 1 или (-oо, 1). <br> |
| | | | |
| - | Свойства числовых неравенств позволяют руководствоваться при решении неравенств следующими правилами: <br> | + | Свойства числовых неравенств позволяют руководствоваться при решении неравенств следующими правилами: <br> |
| | | | |
| - | [[Image:14-06-225.jpg]]<br><br>Применим эти правила для решения линейных неравенств, т. е. неравенств, сводящихся к виду ах + b > 0 (или ах + b < 0), где оиб- любые числа, за одним исключением: [[Image:14-06-226.jpg]]<br>'''Пример 1'''. Решить неравенство Зх - 5 [[Image:14-06-227.jpg]] 7х - 15. <br>Решение. Перенесем член 1х в левую часть неравенства, а член - 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена - 5 (руководствуемся правилом 1). Тогда получим <br>Зх - 7х [[Image:14-06-227.jpg]] - 15 + 5, т. е. - 4х [[Image:14-06-227.jpg]] - 10. <br>Разделим обе части последнего неравенства на одно и то же отрицательное число - 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3). <br>Получим [[Image:14-06-228.jpg]]. Это и есть решение заданного неравенства. <br>Как мы условились, для записи решения можно использовать обозначение соответствующего промежутка числовой прямой: <br>(-oо, 2,5]. <br>О т в е т: [[Image:14-06-228.jpg]], или (-oо, 2,5]. <br>Для неравенств, как и для уравнений, вводится понятие равносильности. Два неравенства f(х) < g(x) и r(x) < s(x) называют равносильными, если они имеют одинаковые решения (или, в частности, если оба неравенства не имеют решений). <br>Обычно при решении неравенства стараются заменить данное неравенство более простым, но равносильным ему. Такую замену называют равносильным преобразованием неравенства. <br> | + | [[Image:14-06-225.jpg|480px|Правила]]<br><br>Применим эти правила для решения '''[[Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций |линейных]]''' неравенств, т. е. неравенств, сводящихся к виду ах + b > 0 (или ах + b < 0), где оиб- любые числа, за одним исключением: [[Image:14-06-226.jpg]]<br> |
| | | | |
| - | Эти преобразования как раз и указаны в сформулированных выше правилах 1—3. <br><br>Пример 2. Решить неравенство <br>
| + | '''Пример 1'''. Решить неравенство Зх - 5 [[Image:14-06-227.jpg]] 7х - 15. <br> |
| | | | |
| - | [[Image:14-06-229.jpg]]<br><br>Решение. Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (правило 2). Это позволит нам освободиться от знаменателей, т. е. перейти к более простому неравенству, равносильному данному:
| + | Решение. Перенесем член 1х в левую часть неравенства, а член - 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена - 5 (руководствуемся правилом 1). Тогда получим <br> |
| | | | |
| - | [[Image:14-06-230.jpg]]<br><br>Воспользовавшись для последнего неравенства правилом 1, получим равносильное ему более простое неравенство: | + | Зх - 7х [[Image:14-06-227.jpg]] - 15 + 5, т. е. - 4х [[Image:14-06-227.jpg]] - 10. |
| | + | |
| | + | Разделим обе части последнего неравенства на одно и то же '''[[Презентація уроку на тему «Додатні та від'ємні числа. Число 0»|отрицательное число]]''' - 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3). |
| | + | |
| | + | Получим [[Image:14-06-228.jpg]]. Это и есть решение заданного неравенства. |
| | + | |
| | + | Как мы условились, для записи решения можно использовать обозначение соответствующего промежутка числовой прямой: |
| | + | |
| | + | (-oо, 2,5]. |
| | + | |
| | + | О т в е т: [[Image:14-06-228.jpg]], или (-oо, 2,5]. |
| | + | |
| | + | Для неравенств, как и для уравнений, вводится понятие равносильности. Два неравенства f(х) < g(x) и r(x) < s(x) называют равносильными, если они имеют одинаковые решения (или, в частности, если оба неравенства не имеют решений). |
| | + | |
| | + | Обычно при решении неравенства стараются заменить данное неравенство более простым, но равносильным ему. Такую замену называют равносильным преобразованием неравенства. <br> |
| | + | |
| | + | Эти преобразования как раз и указаны в сформулированных выше правилах 1—3. <br><br>Пример 2. Решить неравенство <br> |
| | + | |
| | + | [[Image:14-06-229.jpg|180px|Неравенство ]]<br><br>Решение. Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (правило 2). Это позволит нам освободиться от '''[[Задачі до уроку на тему «Зведення дробів до спільного знаменника. Порівняння дробів»|знаменателей]]''', т. е. перейти к более простому неравенству, равносильному данному: |
| | + | |
| | + | [[Image:14-06-230.jpg|320px|Решение]]<br><br>Воспользовавшись для последнего неравенства правилом 1, получим равносильное ему более простое неравенство: |
| | + | |
| | + | 11х - З0х > - 1 + 3, т. е. -17х>2. |
| | + | |
| | + | Наконец, применив правило 3, получим х < [[Image:14-06-231.jpg]] . |
| | + | |
| | + | Ответ: х<[[Image:14-06-231.jpg]], или (-oо,[[Image:14-06-231.jpg]] ). <br>В заключение заметим, что, используя свойства числовых неравенств, мы, конечно, сможем решить не любое неравенство с переменной, а только такое, которое после ряда простейших преобразований (типа тех, что были выполнены в примерах из этого параграфа) принимает вид ах > b (вместо знака > может быть, разумеется, любой другой знак неравенства, строгого или нестрогого). В следующем параграфе мы научимся решать более сложные — квадратные неравенства. <br>''<br>'' |
| | + | |
| | + | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | | | |
| - | <br>11х - ЗОх > - 1 + 3, т. е. -17х>2. <br><br>Наконец, применив правило 3, получим х < [[Image:14-06-231.jpg]] . <br><br>Ответ: х<[[Image:14-06-231.jpg]], или (-oо,[[Image:14-06-231.jpg]] ). <br>В заключение заметим, что, используя свойства числовых неравенств, мы, конечно, сможем решить не любое неравенство с переменной, а только такое, которое после ряда простейших преобразований (типа тех, что были выполнены в примерах из этого параграфа) принимает вид ах > b (вместо знака > может <br>быть, разумеется, любой другой знак неравенства, строгого или нестрогого). В следующем параграфе мы научимся решать более сложные — квадратные неравенства. <br><br><br><br><br>
| |
| | | | |
| - | <br>
| |
| | | | |
| | <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 44: |
Строка 72: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 18:53, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Решение линейных неравенств
Решение линейных неравенств
Свойства числовых равенств помогали нам решать уравнения, т. е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств помогут нам решать неравенства с переменной, т. е. находить те значения переменной, при которых неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной.
Рассмотрим, например, неравенство 2х + 5 < 7.
Подставив вместо х значение 0, получим 5 < 7 — верное неравенство; значит, х = 0 — решение данного неравенства.
Подставив вместо х значение 1, получим 7 < 7 — неверное неравенство; поэтому х = 1 не является решением данного неравенства. Подставив вместо х значение -3, получим -6 + 5 < 7, т.е. -1 < 7 — верное неравенство; следовательно, х = -3 — решение данного неравенства. Подставив вместо х значение 2,5, получим 2-2,5 + 5 < 7, т.е. 10 < 7 — неверное неравенство.
Значит, х = 2,5 не является решением неравенства.
Но вы же понимаете, что это — тупиковый путь: ни один математик не станет так решать неравенство, ведь все числа невозможно перебрать! Вот тут-то и нужно использовать свойства числовых неравенств, рассуждая следующим образом.
Нас интересуют такие числа х, при которых 2х + 5 < 7 — верное числовое неравенство. Но тогда и 2х + 5-5<7-5 — верное неравенство (согласно свойству 2: к обеим частям неравенства прибавили одно и то же число - 5).
Получили более простое неравенство 2х < 2. Разделив обе его части на положительное число 2, получим (на основании свойства 3) верное неравенство х < 1.
Что это значит? Это значит, что решением неравенства является любое число х, которое меньше 1. Эти числа заполняют открытый луч (-oо, 1). . Обычно говорят, что этот луч — решение неравенства 2х + 5 < 7 (точнее было бы говорить о множестве решений, но математики, как всегда, экономны в словах).
Таким образом, можно использовать два варианта записи решений данного неравенства: х < 1 или (-oо, 1).
Свойства числовых неравенств позволяют руководствоваться при решении неравенств следующими правилами:

Применим эти правила для решения линейных неравенств, т. е. неравенств, сводящихся к виду ах + b > 0 (или ах + b < 0), где оиб- любые числа, за одним исключением: 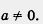
Пример 1. Решить неравенство Зх - 5  7х - 15. 7х - 15.
Решение. Перенесем член 1х в левую часть неравенства, а член - 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена - 5 (руководствуемся правилом 1). Тогда получим
Зх - 7х  - 15 + 5, т. е. - 4х - 15 + 5, т. е. - 4х  - 10. - 10.
Разделим обе части последнего неравенства на одно и то же отрицательное число - 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3).
Получим 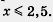 . Это и есть решение заданного неравенства. . Это и есть решение заданного неравенства.
Как мы условились, для записи решения можно использовать обозначение соответствующего промежутка числовой прямой:
(-oо, 2,5].
О т в е т: 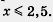 , или (-oо, 2,5]. , или (-oо, 2,5].
Для неравенств, как и для уравнений, вводится понятие равносильности. Два неравенства f(х) < g(x) и r(x) < s(x) называют равносильными, если они имеют одинаковые решения (или, в частности, если оба неравенства не имеют решений).
Обычно при решении неравенства стараются заменить данное неравенство более простым, но равносильным ему. Такую замену называют равносильным преобразованием неравенства.
Эти преобразования как раз и указаны в сформулированных выше правилах 1—3.
Пример 2. Решить неравенство
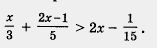
Решение. Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (правило 2). Это позволит нам освободиться от знаменателей, т. е. перейти к более простому неравенству, равносильному данному:
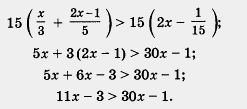
Воспользовавшись для последнего неравенства правилом 1, получим равносильное ему более простое неравенство:
11х - З0х > - 1 + 3, т. е. -17х>2.
Наконец, применив правило 3, получим х < 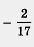 . .
Ответ: х<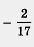 , или (-oо, , или (-oо,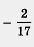 ). ).
В заключение заметим, что, используя свойства числовых неравенств, мы, конечно, сможем решить не любое неравенство с переменной, а только такое, которое после ряда простейших преобразований (типа тех, что были выполнены в примерах из этого параграфа) принимает вид ах > b (вместо знака > может быть, разумеется, любой другой знак неравенства, строгого или нестрогого). В следующем параграфе мы научимся решать более сложные — квадратные неравенства.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Математика для 8 класса, учебники и книги по математике скачать, библиотека онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|