|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Задачи-3(8 класс)</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Задачи, координатами, перпендикуляр, плоскости, точки, параллелограммом, четырехугольник, окружности, уравнение</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Задачи-3(8 класс)''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Задачи-3(8 класс)''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ЗАДАЧИ'''<br> <br><br>1. Проведите оси координат, выберите единицу длины на осях, постройте точки с координатами: (1; 2), (-2; 1). (-1; -3), (2; -1). | + | '''Задачи''' <br><br>1. Проведите оси координат, выберите единицу длины на осях, постройте точки с [[Координатная прямая|координатами]]: (1; 2), (-2; 1). (-1; -3), (2; -1). |
| | | | |
| | 2. Возьмите наудачу четыре точки на плоскости ху. Найдите координаты этих точек. | | 2. Возьмите наудачу четыре точки на плоскости ху. Найдите координаты этих точек. |
| Строка 13: |
Строка 13: |
| | 4. На прямой, перпендикулярной оси х, взяты две точки. У одной из них абсцисса jc = 3. Чему равна абсцисса другой точки? | | 4. На прямой, перпендикулярной оси х, взяты две точки. У одной из них абсцисса jc = 3. Чему равна абсцисса другой точки? |
| | | | |
| - | 5. Из точки А (2; 3) опущен перпендикуляр на ось х. Найдите координаты основания перпендикуляра. | + | 5. Из точки А (2; 3) опущен [[Паралельні та перпендикулярні прямі|перпендикуляр]] на ось х. Найдите координаты основания перпендикуляра. |
| | | | |
| | 6. Через точку А (2; 3) проведена прямая, параллельная оси X. Найдите координаты точки пересечения ее с осью у. | | 6. Через точку А (2; 3) проведена прямая, параллельная оси X. Найдите координаты точки пересечения ее с осью у. |
| Строка 19: |
Строка 19: |
| | 7. Найдите геометрическое место точек плоскости ху, для которых абсцисса х = 3. | | 7. Найдите геометрическое место точек плоскости ху, для которых абсцисса х = 3. |
| | | | |
| - | 8. Найдите геометрическое место точек плоскости ху, для которых IxI = 3. | + | 8. Найдите геометрическое место точек [[Урок 12. Плоские поверхности. Плоскость|плоскости]] ху, для которых IxI = 3. |
| | | | |
| | 9. Даны точки A ( — 3; 2) и В (4; 1). Докажите, что отрезок АВ пересекает ось у, но не пересекает ось х. | | 9. Даны точки A ( — 3; 2) и В (4; 1). Докажите, что отрезок АВ пересекает ось у, но не пересекает ось х. |
| Строка 25: |
Строка 25: |
| | 10. Какую из полуосей оси у (положительную или отрицательную) пересекает отрезок АВ в предыдущей задаче? | | 10. Какую из полуосей оси у (положительную или отрицательную) пересекает отрезок АВ в предыдущей задаче? |
| | | | |
| - | 11. Найдите расстояние от точки ( — 3; 4) до: | + | 11. Найдите расстояние от [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точки]] ( — 3; 4) до: |
| | | | |
| | 1) оси х; 2) оси у. | | 1) оси х; 2) оси у. |
| Строка 45: |
Строка 45: |
| | 3) А (0; 0), С (-2; 2). | | 3) А (0; 0), С (-2; 2). |
| | | | |
| - | 14. Докажите, что четырехугольник ABCD с вершинами в точках А (—1; —2), В (2; —5), С(1; —2), D( —2; 1) является параллелограммом. Найдите точку пересечения его диагоналей. | + | 14. Докажите, что четырехугольник ABCD с вершинами в точках А (—1; —2), В (2; —5), С(1; —2), D( —2; 1) является [[Паралелограм. Ознаки паралелограма. Властивості паралелограма|параллелограммом]]. Найдите точку пересечения его диагоналей. |
| | | | |
| | 15. Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей. | | 15. Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей. |
| Строка 59: |
Строка 59: |
| | 20. Найдите точку, равноудаленную от осей координат и от точки (3; 6). | | 20. Найдите точку, равноудаленную от осей координат и от точки (3; 6). |
| | | | |
| - | 21 Докажите, что четырехугольник ABCD с вершинами в точках А (4; 1), В (0; 4), С (— 3; 0), D (1; — 3) является квадратом. | + | 21 Докажите, что [[Чотирикутник i його елементи|четырехугольник]] ABCD с вершинами в точках А (4; 1), В (0; 4), С (— 3; 0), D (1; — 3) является квадратом. |
| | | | |
| | 22. Докажите, что четыре точки (1; 0), ( — 1; 0), (0; 1), (0; —1) являются вершинами квадрата. | | 22. Докажите, что четыре точки (1; 0), ( — 1; 0), (0; 1), (0; —1) являются вершинами квадрата. |
| Строка 73: |
Строка 73: |
| | 26. Даны точки А {— 1; —1) и С( —4;3). Составьте уравнение окружности с центром в точке С, проходящей через точку А. | | 26. Даны точки А {— 1; —1) и С( —4;3). Составьте уравнение окружности с центром в точке С, проходящей через точку А. |
| | | | |
| - | 27. Найдите центр окружности на оси х, если известно, что окружность проходит через точку (1; 4) и радиус окружности равен 5. | + | 27. Найдите центр [[Окружность, описанная около треугольника. Полные уроки|окружности]] на оси х, если известно, что окружность проходит через точку (1; 4) и радиус окружности равен 5. |
| | | | |
| | 28*. Составьте уравнение окружности с центром в точке (1; 2), касающейся оси х. | | 28*. Составьте уравнение окружности с центром в точке (1; 2), касающейся оси х. |
| Строка 79: |
Строка 79: |
| | 29. Составьте уравнение окружности с центром ( — 3; 4), проходящей через начало координат. | | 29. Составьте уравнение окружности с центром ( — 3; 4), проходящей через начало координат. |
| | | | |
| - | 30*. Какая геометрическая фигура задана уравнением<br>[[Image:22-06-127.jpg]]<br>31. Найдите координаты точек пересечения двух окружностей: х<sup>2</sup>+ у<sup>2</sup> = l, х<sup>2</sup>+ у<sup>2</sup>— 2х + у — 2=0. | + | 30*. Какая геометрическая фигура задана уравнением<br>[[Image:22-06-127.jpg|320px|Уравнение]]<br>31. Найдите координаты точек пересечения двух окружностей: х<sup>2</sup>+ у<sup>2</sup> = l, х<sup>2</sup>+ у<sup>2</sup>— 2х + у — 2=0. |
| | | | |
| | 32. Найдите координаты точек пересечения окружности :х<sup>2</sup>+ у<sup>2</sup> —8x+ 7 = 0 с осью х. | | 32. Найдите координаты точек пересечения окружности :х<sup>2</sup>+ у<sup>2</sup> —8x+ 7 = 0 с осью х. |
| Строка 87: |
Строка 87: |
| | 34. Докажите, что окружность х<sup>2</sup>+ у<sup>2 </sup>+ 2ax = О касается оси у, а [[Image:22-06-97.jpg]] 0. | | 34. Докажите, что окружность х<sup>2</sup>+ у<sup>2 </sup>+ 2ax = О касается оси у, а [[Image:22-06-97.jpg]] 0. |
| | | | |
| - | 35. Составьте уравнение прямой, которая проходит через точки А(— 1; 1), В(1; 0). | + | 35. Составьте [[Уравнение прямой|уравнение]] прямой, которая проходит через точки А(— 1; 1), В(1; 0). |
| | | | |
| | 36. Составьте уравнение прямой АВ, если: | | 36. Составьте уравнение прямой АВ, если: |
| Строка 111: |
Строка 111: |
| | 40. Найдите точку пересечения прямых, заданных уравнениями: | | 40. Найдите точку пересечения прямых, заданных уравнениями: |
| | | | |
| - | 1) х + 2у + 3 = 0, 4x + 5y + 6 = 0;<br>2) Зх —y—2=0, 2х + у — 8 = 0;<br>3) 4x + 5y + 8 = 0, 4x-2y-6 = 0. | + | 1) х + 2у + 3 = 0, 4x + 5y + 6 = 0;<br>2) Зх —y—2=0, 2х + у — 8 = 0;<br>3) 4x + 5y + 8 = 0, 4x-2y-6 = 0. |
| | | | |
| - | 41*. Докажите, что три прямые Х' + 2у = 3, 2х — у = 1 и 3x + y= 4 пересекаются в одной точке. | + | 41*. Докажите, что три прямые Х' + 2у = 3, 2х — у = 1 и 3x + y= 4 пересекаются в одной точке. |
| | | | |
| - | 42*. Найдите координаты точки пересечения медиан треугольника с вершинами (1; 0), (2; 3), (3; 2). | + | 42*. Найдите координаты точки пересечения медиан треугольника с вершинами (1; 0), (2; 3), (3; 2). |
| | | | |
| - | 43. Докажите, что прямые, заданные уравнениями y = kx + l<sub>1</sub><br>y = kx + l<sub>2</sub>, при l<sub>1</sub>[[Image:22-06-97.jpg]]l<sub>2</sub> параллельны. | + | 43. Докажите, что прямые, заданные уравнениями y = kx + l<sub>1</sub><br>y = kx + l<sub>2</sub>, при l<sub>1</sub>[[Image:22-06-97.jpg]]l<sub>2</sub> параллельны. |
| | | | |
| | 44. Среди прямых, заданных уравнениями, укажите пары параллельных прямых: | | 44. Среди прямых, заданных уравнениями, укажите пары параллельных прямых: |
| | | | |
| - | 1) х + у = 1; 2) у = х — 1;3) х-у = 2; 4) у = 4; 5) у = 3; 6) 2х + 2у + 3 = 0. | + | 1) х + у = 1; 2) у = х — 1;3) х-у = 2; 4) у = 4; 5) у = 3; 6) 2х + 2у + 3 = 0. |
| | | | |
| - | 45. Составьте уравнение прямой, которая параллельна оси у и проходит через точку (2; —3). | + | 45. Составьте уравнение прямой, которая параллельна оси у и проходит через точку (2; —3). |
| | | | |
| - | 46. Составьте уравнение прямой, параллельной оси х и проходящей через точку (2; 3). | + | 46. Составьте уравнение прямой, параллельной оси х и проходящей через точку (2; 3). |
| | | | |
| - | 47. Составьте уравнение прямой, проходящей через начало координат и точку (2; 3). | + | 47. Составьте уравнение прямой, проходящей через начало координат и точку (2; 3). |
| | | | |
| - | 48. Найдите угловые коэффициенты прямых из задачи 39.<br> <br>49. Найдите острые углы, которые образует заданная прямая с осью х: | + | 48. Найдите угловые коэффициенты прямых из задачи 39.<br> <br>49. Найдите острые углы, которые образует заданная прямая с осью х: |
| | | | |
| - | 1) 2y= 2x + 3; 2) х[[Image:22-06-128.jpg]] -у = 2; 3) х + у[[Image:22-06-128.jpg]]+ 1 = 0. | + | 1) 2y= 2x + 3; 2) х[[Image:22-06-128.jpg]] -у = 2; 3) х + у[[Image:22-06-128.jpg]]+ 1 = 0. |
| | | | |
| | 50. Найдите точки пересечения окружности jc^ + j/^ = l с прямой: 1) у = 2х+1; 2) у = х + 1; 3) у = Зх + 1; 4) y=kx + l.<br>51*. При каких значениях с прямая х+у + с = 0 к окружность х<sup>2</sup> + у<sup>2</sup>= 1: | | 50. Найдите точки пересечения окружности jc^ + j/^ = l с прямой: 1) у = 2х+1; 2) у = х + 1; 3) у = Зх + 1; 4) y=kx + l.<br>51*. При каких значениях с прямая х+у + с = 0 к окружность х<sup>2</sup> + у<sup>2</sup>= 1: |
| | | | |
| - | 1) пересекаются; 2) не пересекаются; 3) касаются? | + | 1) пересекаются; 2) не пересекаются; 3) касаются? |
| | | | |
| - | 52. Найдите синус, косинус и тангенс углов: 1) 120°; 2) 135°; 3) 150°. | + | 52. Найдите синус, косинус и тангенс углов: 1) 120°; 2) 135°; 3) 150°. |
| | | | |
| - | 53. Найдите: 1) sin 160°; 2) cos 140°; 3) tg 130°. | + | 53. Найдите: 1) sin 160°; 2) cos 140°; 3) tg 130°. |
| | | | |
| - | 54. Найдите синус, косинус и тангенс углов: 1) 40°; 2) 14°36'; 3) 70°20'; 4) 30°16'; 5) 130°; 6) 150°30'; 7) 150°33'; 8) 170°28'. | + | 54. Найдите синус, косинус и тангенс углов: 1) 40°; 2) 14°36'; 3) 70°20'; 4) 30°16'; 5) 130°; 6) 150°30'; 7) 150°33'; 8) 170°28'. |
| | | | |
| - | 55. Найдите углы, для которых: 1) sin а = 0,2; 2) cos а = — 0,7; 3) tga= —0,4. | + | 55. Найдите углы, для которых: 1) sin а = 0,2; 2) cos а = — 0,7; 3) tga= —0,4. |
| | | | |
| | + | [[Image:22-06-129.jpg|480px|Задание]] |
| | | | |
| | + | 57. Найдите cos а и tg а, если: 1) sin а = 0,6, 0°<а<90°; [[Image:22-06-130.jpg|420px|Задание]] |
| | | | |
| | + | 58. Известно, что [[Image:22-06-131.jpg|Задание]] Найдите sin а и cos а. |
| | | | |
| | + | 59. Постройте угол а, если известно, что sin [[Image:22-06-132.jpg|Задание]] |
| | + | |
| | + | 60. Постройте угол а, если известно, что cos [[Image:22-06-133.jpg|Задание]] |
| | + | |
| | + | 61*. Докажите, что если cos a=cos [[Image:22-06-134.jpg]], то а = [[Image:22-06-134.jpg]]. |
| | + | |
| | + | 62*. Докажите, что если sin а = sin [[Image:22-06-134.jpg]], то либо а = [[Image:22-06-134.jpg]], либо а = = 180° —[[Image:22-06-134.jpg]]. |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | 56. Найдите sin а и tg а, если: 1) cos ; 2) cos а = —0,5; 3) cosa=^; 4) cosa=—^.<br> <br>57. Найдите cos а и tg а, если: 1) sin а = 0,6, 0°<а<90°; 2) sina=4-, 90°<а<180°; 3) sin а=^, 0°<а<180°.<br>58. Известно, что tg а= —Найдите sin а и cos а.<br>59. Постройте угол а, если известно, что sin а=—.<br>60. Постройте угол а, если известно, что cos а = —=-.<br>5<br>61*. Докажите, что если cos a=cos р, то а = р. 62*. Докажите, что если sin а = sin р, то либо а = р, либо а = = 180° —р.<br><br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планы конспектов уроков по математике 8 класса [[Математика|скачать]], учебники и книги бесплатно, разработки уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Планы конспектов уроков по математике 8 класса [[Математика|скачать]], учебники и книги бесплатно, разработки уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 158: |
Строка 168: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:25, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Задачи-3(8 класс)
Задачи
1. Проведите оси координат, выберите единицу длины на осях, постройте точки с координатами: (1; 2), (-2; 1). (-1; -3), (2; -1).
2. Возьмите наудачу четыре точки на плоскости ху. Найдите координаты этих точек.
3. На прямой, параллельной оси х, взяты две точки. У одной из них ордината у = 2. Чему равна ордината другой точки?
4. На прямой, перпендикулярной оси х, взяты две точки. У одной из них абсцисса jc = 3. Чему равна абсцисса другой точки?
5. Из точки А (2; 3) опущен перпендикуляр на ось х. Найдите координаты основания перпендикуляра.
6. Через точку А (2; 3) проведена прямая, параллельная оси X. Найдите координаты точки пересечения ее с осью у.
7. Найдите геометрическое место точек плоскости ху, для которых абсцисса х = 3.
8. Найдите геометрическое место точек плоскости ху, для которых IxI = 3.
9. Даны точки A ( — 3; 2) и В (4; 1). Докажите, что отрезок АВ пересекает ось у, но не пересекает ось х.
10. Какую из полуосей оси у (положительную или отрицательную) пересекает отрезок АВ в предыдущей задаче?
11. Найдите расстояние от точки ( — 3; 4) до:
1) оси х; 2) оси у.
12. Найдите координаты середины отрезка АВ, если:
1) A (1; -2), В (5; 6);
2) А (-3; 4), В (1; 2);
3) А (5; 7), В ( — 3; —5).
13. Точка С — середина отрезка АВ. Найдите координаты второго конца отрезка АВ, если:
1) А (0; 1), С ( — 1; 2);
2) А (-1; 3), С (1; -1);
3) А (0; 0), С (-2; 2).
14. Докажите, что четырехугольник ABCD с вершинами в точках А (—1; —2), В (2; —5), С(1; —2), D( —2; 1) является параллелограммом. Найдите точку пересечения его диагоналей.
15. Даны три вершины параллелограмма ABCD: А (1; 0), В (2; 3), С (3; 2). Найдите координаты четвертой вершины D и точки пересечения диагоналей.
16. Найдите середины сторон треугольника с вершинами в точках О (0; 0), А (0; 2), В (-4; 0).
17. Даны три точки А (4; -2), В(1; 2), С (-2; 6). Найдите расстояния между этими точками, взятыми попарно.
18. Докажите, что точки А, В, С в задаче 17 лежат на одной прямой. Какая из них лежит между двумя другими?
19. Найдите на оси х точку, равноудаленную от точек (1; 2) и (2; 3).
20. Найдите точку, равноудаленную от осей координат и от точки (3; 6).
21 Докажите, что четырехугольник ABCD с вершинами в точках А (4; 1), В (0; 4), С (— 3; 0), D (1; — 3) является квадратом.
22. Докажите, что четыре точки (1; 0), ( — 1; 0), (0; 1), (0; —1) являются вершинами квадрата.
23. Какие из точек (1; 2), (3; 4), ( — 4; 3), (О; 5), (5; —1) лежат на окружности, заданной уравнением
х2+ у2=25?
24. Найдите на окружности, заданной уравнением х2+ у2 = 25, точки:
1) с абсциссой 5; 2) с ординатой —12.
25. Даны точки A (2; 0) и В ( — 2; 6). Составьте уравнение окружности, диаметром которой является отрезок АВ.
26. Даны точки А {— 1; —1) и С( —4;3). Составьте уравнение окружности с центром в точке С, проходящей через точку А.
27. Найдите центр окружности на оси х, если известно, что окружность проходит через точку (1; 4) и радиус окружности равен 5.
28*. Составьте уравнение окружности с центром в точке (1; 2), касающейся оси х.
29. Составьте уравнение окружности с центром ( — 3; 4), проходящей через начало координат.
30*. Какая геометрическая фигура задана уравнением
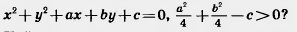
31. Найдите координаты точек пересечения двух окружностей: х2+ у2 = l, х2+ у2— 2х + у — 2=0.
32. Найдите координаты точек пересечения окружности :х2+ у2 —8x+ 7 = 0 с осью х.
33. Докажите, что окружность х2+ у2 + 2ax +1 = О, |aI>1, не пересекается с осью у.
34. Докажите, что окружность х2+ у2 + 2ax = О касается оси у, а 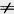 0. 0.
35. Составьте уравнение прямой, которая проходит через точки А(— 1; 1), В(1; 0).
36. Составьте уравнение прямой АВ, если:
1) А (2; 3), В (3; 2);
2) А (4; -1), В (-6; 2);
3) А (5; -3), В (-1; -2).
37. Составьте уравнения прямых, содержащих стороны треугольника ОАВ в задаче 16.
38. Чему равны координаты с и b в уравнении прямой ах + bу = 1, если известно, что она проходит через точки (1; 2) и (2; 1)?
39. Найдите точки пересечения с осями координат прямой заданной уравнением:
1) х + 2у + 3 = 0;
2) 3x + 4y = 12;
3) Зх — 2у + 6 = 0;
4) 4x —2y—10 = 0.
40. Найдите точку пересечения прямых, заданных уравнениями:
1) х + 2у + 3 = 0, 4x + 5y + 6 = 0;
2) Зх —y—2=0, 2х + у — 8 = 0;
3) 4x + 5y + 8 = 0, 4x-2y-6 = 0.
41*. Докажите, что три прямые Х' + 2у = 3, 2х — у = 1 и 3x + y= 4 пересекаются в одной точке.
42*. Найдите координаты точки пересечения медиан треугольника с вершинами (1; 0), (2; 3), (3; 2).
43. Докажите, что прямые, заданные уравнениями y = kx + l1
y = kx + l2, при l1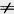 l2 параллельны. l2 параллельны.
44. Среди прямых, заданных уравнениями, укажите пары параллельных прямых:
1) х + у = 1; 2) у = х — 1;3) х-у = 2; 4) у = 4; 5) у = 3; 6) 2х + 2у + 3 = 0.
45. Составьте уравнение прямой, которая параллельна оси у и проходит через точку (2; —3).
46. Составьте уравнение прямой, параллельной оси х и проходящей через точку (2; 3).
47. Составьте уравнение прямой, проходящей через начало координат и точку (2; 3).
48. Найдите угловые коэффициенты прямых из задачи 39.
49. Найдите острые углы, которые образует заданная прямая с осью х:
1) 2y= 2x + 3; 2) х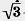 -у = 2; 3) х + у -у = 2; 3) х + у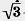 + 1 = 0. + 1 = 0.
50. Найдите точки пересечения окружности jc^ + j/^ = l с прямой: 1) у = 2х+1; 2) у = х + 1; 3) у = Зх + 1; 4) y=kx + l.
51*. При каких значениях с прямая х+у + с = 0 к окружность х2 + у2= 1:
1) пересекаются; 2) не пересекаются; 3) касаются?
52. Найдите синус, косинус и тангенс углов: 1) 120°; 2) 135°; 3) 150°.
53. Найдите: 1) sin 160°; 2) cos 140°; 3) tg 130°.
54. Найдите синус, косинус и тангенс углов: 1) 40°; 2) 14°36'; 3) 70°20'; 4) 30°16'; 5) 130°; 6) 150°30'; 7) 150°33'; 8) 170°28'.
55. Найдите углы, для которых: 1) sin а = 0,2; 2) cos а = — 0,7; 3) tga= —0,4.
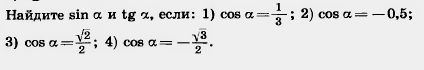
57. Найдите cos а и tg а, если: 1) sin а = 0,6, 0°<а<90°; 
58. Известно, что 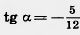 Найдите sin а и cos а. Найдите sin а и cos а.
59. Постройте угол а, если известно, что sin 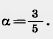
60. Постройте угол а, если известно, что cos 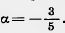
61*. Докажите, что если cos a=cos 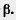 , то а = , то а = 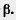 . .
62*. Докажите, что если sin а = sin 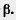 , то либо а = , то либо а = 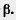 , либо а = = 180° — , либо а = = 180° —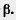 . .
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планы конспектов уроков по математике 8 класса скачать, учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|