|
|
| (2 промежуточные версии не показаны) |
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сонаправленность полупрямых</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сонаправленность полупрямых, полупрямые, параллельный перенос, формулами</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Сонаправленность полупрямых''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Сонаправленность полупрямых''' |
| | + | |
| | + | <br>'''Сонаправленность полупрямых''' <br> <br> Две [[Полупрямая|полупрямые]] называются одинаково направленными или сонаправленными, если они совмещаются параллельным переносом. То есть существует параллельный перенос, который переводит одну полупрямую в другую. |
| | + | |
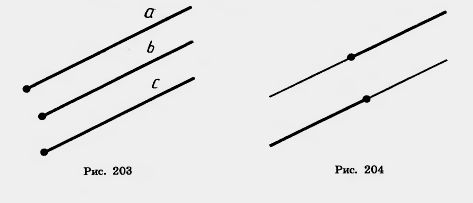
| | + | Если полупрямые а и b одинаково направлены и полупрямые b и с одинаково направлены, то полупрямые а и с тоже одинаково направлены (рис. 203). |
| | + | |
| | + | Действительно, пусть [[Ілюстрації: Поворот. Паралельне перенесення|параллельный перенос]], задаваемый формулами |
| | + | |
| | + | х'=х + m, у'=-у + n, (*) |
| | + | |
| | + | переводит полупрямую а в полупрямую b, а параллельный перенос, задаваемый формулами |
| | + | |
| | + | х"=х' + m<sub>1</sub> у" = у' + n<sub>1</sub> (**) |
| | + | |
| | + | переводит полупрямую b в полупрямую с. |
| | + | |
| | + | Рассмотрим параллельный перенос, задаваемый [[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулами]] |
| | + | |
| | + | х" = х + m + m<sub>1</sub>, у" = у + n + n<sub>1</sub>. (***) <br> <br> Утверждаем, что этот параллельный перенос переводит полупрямую с в полупрямую с. Докажем это. |
| | + | |
| | + | [[Image:22-06-152.jpg|480px|Сонаправленность полупрямых ]]<br> <br> Пусть (х; у) — произвольная точка полупрямой о. Согласно формулам (*) точка 9х + m; у + n) принадлежит полупрямой b. Так как точка (х+m; у + n) принадлежит полупрямой b, то согласно формулам (**) точка (x + m + m<sub>1</sub>; у + n + n<sub>1</sub>) принадлежит полупрямой с. Таким образом, параллельный перенос, задаваемый формулами (***), переводит полупрямую о в полупрямую с. А это значит, что полупрямые о и с одинаково направлены, что и требовалось доказать. |
| | + | |
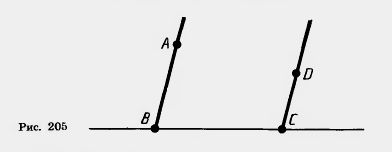
| | + | Две полупрямые называются противоположно направленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой (рис. 204). |
| | + | |
| | + | '''Задача (32)'''. Прямые АВ и CD параллельны. Точки А и D лежат по одну сторону секущей ВС. Докажите, что лучи ВА и CD одинаково направлены. <br><br> [[Image:22-06-153.jpg|320px|Сонаправленность полупрямых ]] <br><br> '''Решение'''. Подвергнем луч CD параллельному переносу, при котором точка С переходит в точку В (рис. 205). При этом прямая CD совместится с прямой ВА. Точка D, смещаясь по прямой, параллельной СВ, остается в той же полуплоскости относительно прямой ВС. Поэтому луч CD совместится с лучом ВА, а значит, эти лучи одинаково направлены. <br> <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| | | | |
| - | '''СОНАПРАВЛЕННОСТЬ ПОЛУПРЯМЫХ'''
| |
| - | <br>
| |
| - |
| |
| - | <br>
| |
| - | Две полупрямые называются одинаково направленными или сонаправленными, если они совмещаются параллельным переносом. То есть существует параллельный перенос, который переводит одну полупрямую в другую.
| |
| - | <br>
| |
| - | Если полупрямые а и b одинаково направлены и полупрямые Ь и с одинаково направлены, то полупрямые а и с тоже одинаково направлены (рис. 203).
| |
| - | <br>
| |
| - | Действительно, пусть параллельный перенос, задаваемый формулами
| |
| - | <br>
| |
| - | х'=х + т, у'=-у + п, (*)
| |
| - | <br>
| |
| - | переводит полупрямую а в полупрямую Ь, а параллельный перенос, задаваемый формулами
| |
| - | <br>
| |
| - | х"^х' + ти у" = у' + пи (**)
| |
| - | <br>
| |
| - | переводит полупрямую Ь в полупрямую с.
| |
| - | <br>
| |
| - | Рассмотрим параллельный перенос, задаваемый формулами
| |
| - | <br>
| |
| - | х" = х-\-т + т1, у" = у + п-\-п\. (***)
| |
| - | <br>
| |
| - |
| |
| - | <br>
| |
| - | Утверждаем, что этот параллельный перенос переводит полупрямую с в полупрямую с. Докажем это.
| |
| - | <br>
| |
| - | а
| |
| - | <br>
| |
| - |
| |
| - | <br>
| |
| - | Пусть {х\ у) — произвольная точка полупрямой о. Согласно формулам (*) точка {х-\-т; у + п) принадлежит полупрямой Ь. Так как точка {х+т; у + п) принадлежит полупрямой Ь, то согласно формулам (**) точка (дс + т + т,; у-\-п-\-П[) принадлежит полупрямой с. Таким образом, параллельный перенос, задаваемый формулами (***), переводит полупрямую о в полупрямую с. А это значит, что полупрямые о и с одинаково направлены, что и требовалось доказать.
| |
| - | <br>
| |
| - | Две полупрямые называются противоположно направленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой (рис. 204).
| |
| - | <br>
| |
| - | Задача (32). Прямые АВ и CD параллельны. Точки А и D лежат по одну сторону секущей ВС. Докажите, что лучи ВА и CD одинаково направлены.
| |
| - | <br>
| |
| - |
| |
| - | <br><br>
| |
| - | Рис. 205
| |
| - | <br>
| |
| - |
| |
| - | <br><br>
| |
| - | Решение. Подвергнем луч CD параллельному переносу, при котором точка С переходит в точку В (рис. 205). При этом прямая CD совместится с прямой ВА. Точка D, смещаясь по прямой, параллельной СВ, остается в той же полуплоскости относительно прямой ВС. Поэтому луч CD совместится с лучом ВА, а значит, эти лучи одинаково направлены.
| |
| - | <br><br><br>
| |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Учебники по всему предметам [[Математика|скачать]], разработка планов уроков для учителей, Математика для 8 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Учебники по всему предметам [[Математика|скачать]], разработка планов уроков для учителей, Математика для 8 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 55: |
Строка 34: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Если полупрямые а и b одинаково направлены и полупрямые b и с одинаково направлены, то полупрямые а и с тоже одинаково направлены (рис. 203).
переводит полупрямую а в полупрямую b, а параллельный перенос, задаваемый формулами
переводит полупрямую b в полупрямую с.
Две полупрямые называются противоположно направленными, если каждая из них одинаково направлена с полупрямой, дополнительной к другой (рис. 204).
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.