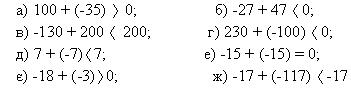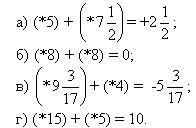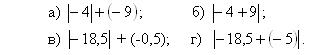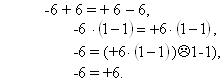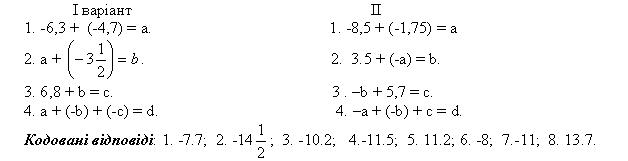|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>математика, 6 клас, клас, урок, на тему, урок на тему, додавання від'ємних раціональних чисел, конспект уроку</metakeywords> | + | <metakeywords>математика, 6 клас, клас, урок, на тему, урок на тему, додавання від'ємних раціональних чисел, конспект уроку</metakeywords> |
| | | | |
| - | Конспект уроку з математики для 6 класу | + | '''Конспект уроку з [[Математика_6_клас|математики для 6 класу]]''' |
| | | | |
| - | <br>'''Тема.''' Додавання раціональних чисел. | + | <br>'''Тема.''' [[Додавання_від'ємних_раціональних_чисел|'''''Додавання раціональних чисел.''''']] |
| | | | |
| - | <br>''Мета:'' формувати в учнів навички і вміння додавати раціональні числа; <br> розвивати кмітливість, упевненість у власних силах, уміння міркувати; <br> виховувати дисциплінованість, повагу до товаришів, інтерес до предмета і навчання. | + | <br>''Мета:'' формувати в учнів навички і вміння додавати раціональні числа; <br> розвивати кмітливість, упевненість у власних силах, уміння міркувати; <br> виховувати дисциплінованість, повагу до товаришів, інтерес до предмета і навчання. |
| | | | |
| | ''<br>Обладнання:'' гральні кубики, таблиця «Додавання раціональних чисел», картки з кодованими вправами.<br><br> ''ХІД УРОКУ'' <br>I. Організаційний момент.<br>II. П’ятихвилинки для життя.(1-4слайди)<br>IIІ. Актуалізація опорних знань.<br><br>1. Фронтальне опитування. | | ''<br>Обладнання:'' гральні кубики, таблиця «Додавання раціональних чисел», картки з кодованими вправами.<br><br> ''ХІД УРОКУ'' <br>I. Організаційний момент.<br>II. П’ятихвилинки для життя.(1-4слайди)<br>IIІ. Актуалізація опорних знань.<br><br>1. Фронтальне опитування. |
| | | | |
| - | <br>1. Як додати два числа з однаковими знаками? З різними?<br>2. Чому дорівнює сума протилежних чисел?<br>3. До числа а додали від’ємне число. Як змінилося число а?<br>4. Чи може сума двох чисел бути меншою від доданка?<br>5. Збільшується чи зменшується число, якщо його додати до додатного числа? Від’ємного ? до числа нуль?<br>[[Image:asd8.jpg]]<br>7. Із наведених прикладів виберіть неправильні рівності або нерівності(5слайд)<br> [[Image:asd9.jpg]]<br>3. Гра «Хто швидше»<br> Замість зірочок поставте знаки «+» або «-».<br>[[Image:asd10.jpg]]<br><br>ІV. Розв’язування вправ.<br> Виконуючи додавання двох раціональних чисел, спочатку встановлюємо, яким числом – додатним чи від’ємним – є сума двох чисел. Потім знаходимо модуль суми. | + | <br>1. Як додати два числа з однаковими знаками? З різними?<br>2. Чому дорівнює сума протилежних чисел?<br>3. До числа а додали від’ємне число. Як змінилося число а?<br>4. Чи може сума двох чисел бути меншою від доданка?<br>5. Збільшується чи зменшується число, якщо його додати до додатного числа? Від’ємного ? до числа нуль?<br>[[Image:Asd8.jpg]]<br>7. Із наведених прикладів виберіть неправильні рівності або нерівності(5слайд)<br> [[Image:Asd9.jpg]]<br>3. Гра «Хто швидше»<br> Замість зірочок поставте знаки «+» або «-».<br>[[Image:Asd10.jpg]]<br><br>ІV. Розв’язування вправ.<br> Виконуючи додавання двох раціональних чисел, спочатку встановлюємо, яким числом – додатним чи від’ємним – є сума двох чисел. Потім знаходимо модуль суми. |
| | | | |
| - | <br>1. Знайти значення виразів:<br>[[Image:asd11.jpg]] | + | <br>1. Знайти значення виразів:<br>[[Image:Asd11.jpg]] |
| | | | |
| - | <br> 2. Виконання вправ з підручника.<br> № 1033(усно).<br> № 1042 (а,б) (два учні з коментуванням).<br> № 1045(колективне розв’язування).<br> <br><br> 3.Софізм. Будь-яке від’ємне число дорівнює додатному:<br> [[Image:asd12.jpg]]<br>Де помилка? | + | <br> 2. Виконання вправ з підручника.<br> № 1033(усно).<br> № 1042 (а,б) (два учні з коментуванням).<br> № 1045(колективне розв’язування).<br> <br><br> 3.Софізм. Будь-яке від’ємне число дорівнює додатному:<br> [[Image:Asd12.jpg]]<br>Де помилка? |
| | | | |
| - | <br>Відповідь: Ділити на нуль (1-1=0) не можна.<br><br>4. Кодовані вправи.<br> Виконавши першу вправу, учень підставляє результат у другу умову, а також шукає одержане число серед відповідей. Якщо його там немає – допущено помилку. Виконавши одна за одною всі вправи свого варіанта, учень здає роботу вчителю на перевірку за кодованою відповіддю. Наприклад, 7,2,1,5. Це означає, що а = -11, b = 14,5, c = -7,7, d =-11. | + | <br>Відповідь: Ділити на нуль (1-1=0) не можна.<br><br>4. Кодовані вправи.<br> Виконавши першу вправу, учень підставляє результат у другу умову, а також шукає одержане число серед відповідей. Якщо його там немає – допущено помилку. Виконавши одна за одною всі вправи свого варіанта, учень здає роботу вчителю на перевірку за кодованою відповіддю. Наприклад, 7,2,1,5. Це означає, що а = -11, b = 14,5, c = -7,7, d =-11. |
| | | | |
| - | [[Image:asd13.jpg]]<br> <br>Таких завдань має бути на кожного учня. Відповідь наведено для першого варіанту.<br><br>5. Цікаві вправи.<br>1.Обчислити |a+b+c| , якщо a=-3,b=-10,c=-2.<br><br>2.На конкурсі «Веселі козачата» команда отримала спочатку 4 штрафних очки, а потім ще 2. На скільки очок погіршився результат команди?<br><br>3. Замість зірочок запишіть такі числа, щоб отримати правильні розв’язки .<br> а) -* + * = -18;<br> б) -* + * =10<br> в) * + (-*) = 23;<br> г) - * + * =-1;<br> д) * - (-*) = 0;<br> е) * + (-*) = -54.<br><br>4. Сума двох послідовних чисел дорівнює – 17. Знайдіть ці числа.<br><br>V. Підсумок уроку.<br><br>VI. Домашнє завдання.<br>За підручником п.35, Г.Янченко, В.Кравчук, № 1036, 1038, 1047.<br><br>''Цікаво знати''<br>Виникли від’ємні числа в Китаї в І ст. до н.е. у зв’язку з розв’язуванням рівнянь для раціоналізації обчислень. Тоді від’ємні числа, на відміну від додатних, зображали іншим кольором. Додатними числами позначали майно, наявні гроші, прибуток. Їм раділи і зображали їх червоним кольором (китайці їх називали «чен»), від’ємними числами позначали борг, збиток і зображали їх чорним кольором (їх називали «фу»). | + | [[Image:Asd13.jpg]]<br> <br>Таких завдань має бути на кожного учня. Відповідь наведено для першого варіанту.<br><br>5. Цікаві вправи.<br>1.Обчислити |a+b+c| , якщо a=-3,b=-10,c=-2.<br><br>2.На конкурсі «Веселі козачата» команда отримала спочатку 4 штрафних очки, а потім ще 2. На скільки очок погіршився результат команди?<br><br>3. Замість зірочок запишіть такі числа, щоб отримати правильні розв’язки .<br> а) -* + * = -18;<br> б) -* + * =10<br> в) * + (-*) = 23;<br> г) - * + * =-1;<br> д) * - (-*) = 0;<br> е) * + (-*) = -54.<br><br>4. Сума двох послідовних чисел дорівнює – 17. Знайдіть ці числа.<br><br>V. Підсумок уроку.<br><br>VI. Домашнє завдання.<br>За підручником п.35, Г.Янченко, В.Кравчук, № 1036, 1038, 1047.<br><br>''Цікаво знати''<br>Виникли від’ємні числа в Китаї в І ст. до н.е. у зв’язку з розв’язуванням рівнянь для раціоналізації обчислень. Тоді від’ємні числа, на відміну від додатних, зображали іншим кольором. Додатними числами позначали майно, наявні гроші, прибуток. Їм раділи і зображали їх червоним кольором (китайці їх називали «чен»), від’ємними числами позначали борг, збиток і зображали їх чорним кольором (їх називали «фу»). |
| | | | |
| - | <br>Індійські математики Брахмагупта (VII cт.) і Бхаскара (ХІІ ст) використовували такі правила дій для від’ємних і додатних чисел: <br> «Сума майна і майна є майно».<br> «Сума двох боргів є борг».<br> «Сума майна і боргу дорівнює їх різниці».<br> «Сума майна і такого самого боргу дорівнює нулю». | + | <br>Індійські математики Брахмагупта (VII cт.) і Бхаскара (ХІІ ст) використовували такі правила дій для від’ємних і додатних чисел: <br> «Сума майна і майна є майно».<br> «Сума двох боргів є борг».<br> «Сума майна і боргу дорівнює їх різниці».<br> «Сума майна і такого самого боргу дорівнює нулю». |
| | | | |
| - | <br>Але довгий час від’ємних не визнавали, вважали їх не справжніми, фіктивними. Бхаскара так писав: «Люди не схвалюють від’ємних чисел». | + | <br>Але довгий час від’ємних не визнавали, вважали їх не справжніми, фіктивними. Бхаскара так писав: «Люди не схвалюють від’ємних чисел». |
| | | | |
| - | <br>Сучасне позначення додатних і від’ємних чисел знаками «+» і «-» ввів наприкінці XV ст. німецький математик Я.Відман. <br> ''<br>Надіслано вчителями Міжнародного ліцею "Гранд"'' | + | <br>Сучасне позначення додатних і від’ємних чисел знаками «+» і «-» ввів наприкінці XV ст. німецький математик Я.Відман. <br> ''<br>Надіслано вчителями Міжнародного ліцею "Гранд"'' |
| - | [[категория: Додавання від'ємних раціональних чисел. Конспект уроку і опорний каркас]] | + | |
| | + | [[Category:Додавання_від'ємних_раціональних_чисел._Конспект_уроку_і_опорний_каркас]] |
Текущая версия на 10:12, 27 января 2010
Конспект уроку з математики для 6 класу
Тема. Додавання раціональних чисел.
Мета: формувати в учнів навички і вміння додавати раціональні числа;
розвивати кмітливість, упевненість у власних силах, уміння міркувати;
виховувати дисциплінованість, повагу до товаришів, інтерес до предмета і навчання.
Обладнання: гральні кубики, таблиця «Додавання раціональних чисел», картки з кодованими вправами.
ХІД УРОКУ
I. Організаційний момент.
II. П’ятихвилинки для життя.(1-4слайди)
IIІ. Актуалізація опорних знань.
1. Фронтальне опитування.
1. Як додати два числа з однаковими знаками? З різними?
2. Чому дорівнює сума протилежних чисел?
3. До числа а додали від’ємне число. Як змінилося число а?
4. Чи може сума двох чисел бути меншою від доданка?
5. Збільшується чи зменшується число, якщо його додати до додатного числа? Від’ємного ? до числа нуль?
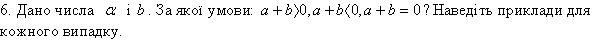
7. Із наведених прикладів виберіть неправильні рівності або нерівності(5слайд)
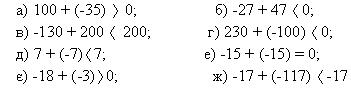
3. Гра «Хто швидше»
Замість зірочок поставте знаки «+» або «-».
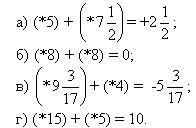
ІV. Розв’язування вправ.
Виконуючи додавання двох раціональних чисел, спочатку встановлюємо, яким числом – додатним чи від’ємним – є сума двох чисел. Потім знаходимо модуль суми.
1. Знайти значення виразів:
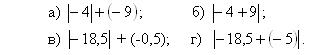
2. Виконання вправ з підручника.
№ 1033(усно).
№ 1042 (а,б) (два учні з коментуванням).
№ 1045(колективне розв’язування).
3.Софізм. Будь-яке від’ємне число дорівнює додатному:
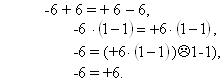
Де помилка?
Відповідь: Ділити на нуль (1-1=0) не можна.
4. Кодовані вправи.
Виконавши першу вправу, учень підставляє результат у другу умову, а також шукає одержане число серед відповідей. Якщо його там немає – допущено помилку. Виконавши одна за одною всі вправи свого варіанта, учень здає роботу вчителю на перевірку за кодованою відповіддю. Наприклад, 7,2,1,5. Це означає, що а = -11, b = 14,5, c = -7,7, d =-11.
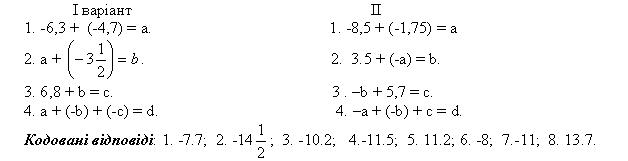
Таких завдань має бути на кожного учня. Відповідь наведено для першого варіанту.
5. Цікаві вправи.
1.Обчислити |a+b+c| , якщо a=-3,b=-10,c=-2.
2.На конкурсі «Веселі козачата» команда отримала спочатку 4 штрафних очки, а потім ще 2. На скільки очок погіршився результат команди?
3. Замість зірочок запишіть такі числа, щоб отримати правильні розв’язки .
а) -* + * = -18;
б) -* + * =10
в) * + (-*) = 23;
г) - * + * =-1;
д) * - (-*) = 0;
е) * + (-*) = -54.
4. Сума двох послідовних чисел дорівнює – 17. Знайдіть ці числа.
V. Підсумок уроку.
VI. Домашнє завдання.
За підручником п.35, Г.Янченко, В.Кравчук, № 1036, 1038, 1047.
Цікаво знати
Виникли від’ємні числа в Китаї в І ст. до н.е. у зв’язку з розв’язуванням рівнянь для раціоналізації обчислень. Тоді від’ємні числа, на відміну від додатних, зображали іншим кольором. Додатними числами позначали майно, наявні гроші, прибуток. Їм раділи і зображали їх червоним кольором (китайці їх називали «чен»), від’ємними числами позначали борг, збиток і зображали їх чорним кольором (їх називали «фу»).
Індійські математики Брахмагупта (VII cт.) і Бхаскара (ХІІ ст) використовували такі правила дій для від’ємних і додатних чисел:
«Сума майна і майна є майно».
«Сума двох боргів є борг».
«Сума майна і боргу дорівнює їх різниці».
«Сума майна і такого самого боргу дорівнює нулю».
Але довгий час від’ємних не визнавали, вважали їх не справжніми, фіктивними. Бхаскара так писав: «Люди не схвалюють від’ємних чисел».
Сучасне позначення додатних і від’ємних чисел знаками «+» і «-» ввів наприкінці XV ст. німецький математик Я.Відман.
Надіслано вчителями Міжнародного ліцею "Гранд"
Предмети > Математика > Математика 6 клас > Додавання від'ємних раціональних чисел > Додавання від'ємних раціональних чисел. Конспект уроку і опорний каркас
|