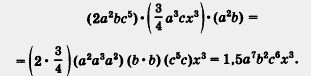|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | '''УМНОЖЕНИЕ ОДНОЧЛЕНОВ. ВОЗВЕДЕНИЕ ОДНОЧЛЕНА В НАТУРАЛЬНУЮ СТЕПЕНЬ ''' |
| - | '''УМНОЖЕНИЕ ОДНОЧЛЕНОВ. ВОЗВЕДЕНИЕ ОДНОЧЛЕНА В НАТУРАЛЬНУЮ СТЕПЕНЬ ''' | + | |
| | | | |
| | <br>В § 10 мы рассматривали сложение и вычитание одночленов. Оказалось, что эти операции применимы только к подобным одночленам. А как обстоит дело с умножением одночленов? <br>Очень просто: если между двумя одночленами поставить знак умножения, то снова получится одночлен; остается лишь привести его к стандартному виду (фактически это мы уже делали в примере из § 9). Не вызывает затруднений и возведение одночлена в степень. При этом используются правила действий со степенями (фактически в примере 3 из § 7 мы уже возводили одночлен в степень). | | <br>В § 10 мы рассматривали сложение и вычитание одночленов. Оказалось, что эти операции применимы только к подобным одночленам. А как обстоит дело с умножением одночленов? <br>Очень просто: если между двумя одночленами поставить знак умножения, то снова получится одночлен; остается лишь привести его к стандартному виду (фактически это мы уже делали в примере из § 9). Не вызывает затруднений и возведение одночлена в степень. При этом используются правила действий со степенями (фактически в примере 3 из § 7 мы уже возводили одночлен в степень). |
| | | | |
| - | <u>Пример 1.</u> Найти произведение трех одночленов: 2a<sup>2</sup>bc<sup>5</sup>, [[Image:07-06-124.jpg]]<br>Решение. Имеем: <br>[[Image:07-06-125.jpg]]<br><u>Пример 2.</u> Упростить выражение (- 2a<sup>2</sup>bc<sup>3</sup>)<sup>5</sup>(т. е. представить его в виде одночлена). <br>Р е ш е н и е. (- 2a<sup>2</sup>bc<sup>3</sup>)<sup>5</sup> = - 2<sup>5</sup>(a<sup>2</sup>)<sup>5</sup>b<sup>5</sup>(c<sup>3</sup>)<sup>5</sup>=-32a<sup>10</sup>b<sup>5</sup>c15. <br>Мы использовали, во-первых, то, что при возведении произведения в степень надо возвести в эту степень каждый множитель. <br>Поэтому у нас появилась запись 2<sup>5</sup>(a<sup>2</sup>)<sup>5</sup>b5(c<sup>3</sup>)<sup>5</sup>. <br>Во-вторых, мы воспользовались тем, что (- 2)<sup>5</sup> = - 2<sup>5</sup> . <br>В-третьих, мы использовали то, что при возведении степени в степень показатели перемножаются. Поэтому вместо (а<sup>2</sup>)<sup>5</sup> мы написали а<sup>10</sup>, а вместо (с<sup>3</sup>)<sup>5</sup> мы написали с<sup>15</sup>. <br><u>Пример 3.</u> Представить одночлен 36a<sup>2</sup>b<sup>4</sup>c<sup>5</sup> в виде произведения одночленов. <br>Решение. Здесь, как и в примере 2 из § 10, решение не <br>единственно. Вот несколько вариантов решения: <br>36abc<sup>5</sup> = A8a2)-Bb4c5); <br>36a2b4c5 = C6abc) • (аЪ*с*У, <br>36а W - (- ЗЬ4) • (- 12а2с5); <br>()()() <br>Попробуйте сами придумать еще несколько решений приме- <br>ра 3. <br>Пример 4. Представить данный одночлен А в виде В", где <br>В — одночлен, если: <br>а)А = 32о5,га = 5; г)А = - 27a3b9, п = 3; <br>б) А = а3Ъ*. п = 3; д) <br>3.11.1 <br>ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ <br>3.12.1 <br>ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ <br>72с2(Ь2J(с3J = Gcb2c3J, то А = В2, где <br>Решение. <br>а) Имеем: 32с5 - 25с5 = BсM. Значит, А = В5, где В = 2с. <br>б) Имеем: а3Ъ6 = c8(b2K = (cb2K. Следовательно, А = Б3, где <br>B = cb2. <br>в) Так как 49c2b4c6 <br>B=7cbV. <br>г) Поскольку - 27с3Ь9 = (- 3Kс3(Ь3K = (- Зой3K, заключаем, что <br>А - В3, где В - - ЗсЬ3. <br>д) Имеем: 16a8b5 - 24(a2Lb5. <br>Если бы не было множителя Ъъ, то задача решалась бы без <br>труда: <br>16с8 = 24(с2L = Bс2L. <br>Если бы вместо Ьь был множитель Ь12, то мы решили бы задачу <br>так: <br>16a8b12 = 24(с2L(Ь3L - BcVL. <br>Однако множитель Ъь нельзя представить в виде (Ь*L, где k — <br>натуральное число, этот множитель, как говорится, «портит все <br>дело». Значит, одночлен 16с8Ь5 нельзя представить в виде В4, где <br>В — некоторый одночлен, в <br>Пример показывает, что в математике далеко не все всегда полу- <br>чается, не любая задача имеет решение (как и в реальной жизни). <br>Кстати, если математику предлагают решить задачу, которая <br>на самом деле не имеет решения, то он говорит: «Задача постав- <br>лена некорректно» или «Это — некорректная задача». Тот, кто <br>предложил некорректную задачу, должен извиниться. Вот и ав- <br>тор извиняется за пример 4д). Хотя согласитесь, <br>i что он был дан не без пользы. <br>к Раз уж мы заговорили о корректных и некор- <br>Щ ректных задачах, приведем еще несколько приме- <br>? ров и тех, и других, а вы попытайтесь объяснить, <br>' почему задача корректна или некорректна. <br>Корректные задачи: <br>1. Упростить 2cb2'CcbK. <br>2. Упростить 7ab + 8ab + аЬ. <br>3. Вычислить 2>7 + 3'8 . <br>4. Представить одночлен 13a4b5 в виде суммы одночленов. <br>5. Представить одночлен 48х3у*г в виде произведения одно- <br>членов. <br>6. Представить одночлен А - 25с4 в виде квадрата некоторого <br>одночлена В. <br>Некорректные задачи: <br>1. Сложить одночлены ЗсЬ2, ЪаЪ2 и 7с2Ь. <br>2. Вычислить 2'7 + 8'8 . <br>6-6 <br>3. Представить одночлен А в виде квадрата некоторого одно- <br>члена В, если А = - 25а4. <br>4. Представить одночлен А в виде куба некоторого одночлена <br>В, если А — 8с4. <br> | + | <u>Пример 1.</u> Найти произведение трех одночленов: 2a<sup>2</sup>bc<sup>5</sup>, [[Image:07-06-124.jpg]]<br>Решение. Имеем: <br>[[Image:07-06-125.jpg]]<br><u>Пример 2.</u> Упростить выражение (- 2a<sup>2</sup>bc<sup>3</sup>)<sup>5</sup>(т. е. представить его в виде одночлена). <br>Р е ш е н и е. (- 2a<sup>2</sup>bc<sup>3</sup>)<sup>5</sup> = - 2<sup>5</sup>(a<sup>2</sup>)<sup>5</sup>b<sup>5</sup>(c<sup>3</sup>)<sup>5</sup>=-32a<sup>10</sup>b<sup>5</sup>c15. <br>Мы использовали, во-первых, то, что при возведении произведения в степень надо возвести в эту степень каждый множитель. <br>Поэтому у нас появилась запись 2<sup>5</sup>(a<sup>2</sup>)<sup>5</sup>b5(c<sup>3</sup>)<sup>5</sup>. <br>Во-вторых, мы воспользовались тем, что (- 2)<sup>5</sup> = - 2<sup>5</sup> . <br>В-третьих, мы использовали то, что при возведении степени в степень показатели перемножаются. Поэтому вместо (а<sup>2</sup>)<sup>5</sup> мы написали а<sup>10</sup>, а вместо (с<sup>3</sup>)<sup>5</sup> мы написали с<sup>15</sup>. <br><u>Пример 3.</u> Представить одночлен 36a<sup>2</sup>b<sup>4</sup>c<sup>5</sup> в виде произведения одночленов. <br>Решение. Здесь, как и в примере 2 из § 10, решение не <br>единственно. Вот несколько вариантов решения: <br>36a<sup>2</sup>b<sup>4</sup>c<sup>5</sup> =( 18a<sup>2</sup>)•(2b<sup>4</sup>c<sup>5</sup>); <br>36a<sup>2</sup>b<sup>4</sup>c<sup>5</sup> =( 36abc) • (аb<sup>3</sup>с<sup>4</sup>), <br>36а<sup>2</sup> b<sup>4</sup>c<sup>5</sup>= (- Зb<sup>4</sup>) • (- 12а<sup>2</sup>с<sup>5</sup>); <br>36а<sup>2</sup> b<sup>4</sup>c<sup>5</sup>=(2a<sup>3</sup>)•(3bc) •(6b<sup>3</sup>c<sup>4</sup>)<br>Попробуйте сами придумать еще несколько решений примера 3. <br><u>Пример 4</u>. Представить данный одночлен А в виде В", где В — одночлен, если: <br>а)А = 32a<sup>5</sup>,n = 5; <br>б) А = а<sup>3</sup>b<sup>6</sup>. n = 3;<br> |
| | + | |
| | + | в) А =49а<sup>2</sup>b<sup>4</sup>c<sup>6</sup>. n = 2; |
| | + | |
| | + | г) А = - 27a<sup>3</sup>b<sup>9</sup>, n = 3; |
| | + | |
| | + | д) А = 16a<sup>8</sup>b<sup>5</sup>, n = 4; <br> |
| | + | |
| | + | Решение. <br>а) Имеем: 32a<sup>5</sup> - 2<sup>5</sup>a<sup>5</sup> = (2a)<sup>5</sup>. Значит, А = В<sup>5</sup>, где В = 2с. <br>б) Имеем: а<sup>3</sup>b<sup>6</sup> = a<sup>3</sup>(b<sup>2</sup>)<sup>3</sup> = (ab<sup>2</sup>)<sup>3</sup>. Следовательно, А = B<sup>3</sup>, где B = ab<sup>2</sup>. <br>в) Так как 49a<sup>2</sup>b<sup>4</sup>c<sup>6</sup> =7<sup>2</sup>a<sup>2</sup>(b<sup>2</sup>)<sup>2</sup>(c<sup>3</sup>)<sup>3</sup>=(7ab<sup>2</sup>c<sup>3</sup>)<sup>2</sup><br>то А=В<sup>2</sup> , где В=7ab<sup>2</sup>c<sup>3</sup><br>г) Поскольку - 27a<sup>3</sup>b<sup>9</sup> = (- 3)<sup>3</sup>a<sup>3</sup>(b<sup>3</sup>)<sup>3</sup>, заключаем, что А - В<sup>3</sup>, где В - ЗaЬ<sup>3</sup>. <br>д) Имеем: 16a<sup>8</sup> =2<sup>4</sup>(a<sup>2</sup>)<sup>4</sup><sup></sup>=<sup></sup>(2a<sup>2</sup>)<sup>4</sup>. <br>Если бы не было множителя b<sup>5</sup>, то задача решалась бы без труда: <br>16a<sup>8</sup> = 2<sup>4</sup>(a<sup>2</sup>)<sup>4</sup>=(2a<sup>2</sup>)<sup>4</sup> |
| | + | |
| | + | Если бы вместо b<sup>5</sup> был множитель b<sup>12</sup>, то мы решили бы задачу так: <br>16a<sup>8</sup>b<sup>12</sup> = 2<sup>4</sup>(a<sup>2</sup>)<sup>4</sup>(b<sup>3</sup>)<sup>4</sup> =(2a<sup>2</sup>b<sup>3</sup>)<sup>4</sup> |
| | + | |
| | + | Однако множитель b<sup>5</sup> нельзя представить в виде (b<sup>k</sup>)4, где k — натуральное число, этот множитель, как говорится, «портит все дело». Значит, одночлен |
| | + | |
| | + | 16a<sup>8 </sup><sup></sup>b<sup>5</sup> нельзя представить в виде В<sup>4</sup>, где В — некоторый одночлен, в <sup></sup>Пример показывает, что в математике далеко не все всегда получается, не любая задача имеет решение (как и в реальной жизни). |
| | + | |
| | + | Кстати, если математику предлагают решить задачу, которая на самом деле не имеет решения, то он говорит: «Задача поставлена некорректно» или «Это — некорректная задача». Тот, кто предложил некорректную задачу, должен извиниться. Вот и автор извиняется за пример 4д). Хотя согласитесь, i что он был дан не без пользы. |
| | + | |
| | + | Раз уж мы заговорили о корректных и некорректных задачах, приведем еще несколько примеров и тех, и других, а вы попытайтесь объяснить, ' почему задача корректна или некорректна. |
| | | | |
| | + | Корректные задачи: <br>1. Упростить 2cb2'CcbK. <br>2. Упростить 7ab + 8ab + аЬ. <br>3. Вычислить 2>7 + 3'8 . <br>4. Представить одночлен 13a4b5 в виде суммы одночленов. <br>5. Представить одночлен 48х3у*г в виде произведения одно- <br>членов. <br>6. Представить одночлен А - 25с4 в виде квадрата некоторого <br>одночлена В. <br>Некорректные задачи: <br>1. Сложить одночлены ЗсЬ2, ЪаЪ2 и 7с2Ь. <br>2. Вычислить 2'7 + 8'8 . <br>6-6 <br>3. Представить одночлен А в виде квадрата некоторого одно- <br>члена В, если А = - 25а4. <br>4. Представить одночлен А в виде куба некоторого одночлена <br>В, если А — 8с4. <br> |
| | | | |
| | + | <br> |
| | | | |
| | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> <br> | | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> <br> |
Версия 19:23, 7 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Умножение одночленов, Возведение одночлена в натуральную степень
УМНОЖЕНИЕ ОДНОЧЛЕНОВ. ВОЗВЕДЕНИЕ ОДНОЧЛЕНА В НАТУРАЛЬНУЮ СТЕПЕНЬ
В § 10 мы рассматривали сложение и вычитание одночленов. Оказалось, что эти операции применимы только к подобным одночленам. А как обстоит дело с умножением одночленов?
Очень просто: если между двумя одночленами поставить знак умножения, то снова получится одночлен; остается лишь привести его к стандартному виду (фактически это мы уже делали в примере из § 9). Не вызывает затруднений и возведение одночлена в степень. При этом используются правила действий со степенями (фактически в примере 3 из § 7 мы уже возводили одночлен в степень).
Пример 1. Найти произведение трех одночленов: 2a2bc5, 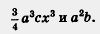
Решение. Имеем:
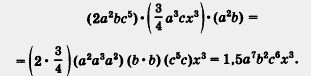
Пример 2. Упростить выражение (- 2a2bc3)5(т. е. представить его в виде одночлена).
Р е ш е н и е. (- 2a2bc3)5 = - 25(a2)5b5(c3)5=-32a10b5c15.
Мы использовали, во-первых, то, что при возведении произведения в степень надо возвести в эту степень каждый множитель.
Поэтому у нас появилась запись 25(a2)5b5(c3)5.
Во-вторых, мы воспользовались тем, что (- 2)5 = - 25 .
В-третьих, мы использовали то, что при возведении степени в степень показатели перемножаются. Поэтому вместо (а2)5 мы написали а10, а вместо (с3)5 мы написали с15.
Пример 3. Представить одночлен 36a2b4c5 в виде произведения одночленов.
Решение. Здесь, как и в примере 2 из § 10, решение не
единственно. Вот несколько вариантов решения:
36a2b4c5 =( 18a2)•(2b4c5);
36a2b4c5 =( 36abc) • (аb3с4),
36а2 b4c5= (- Зb4) • (- 12а2с5);
36а2 b4c5=(2a3)•(3bc) •(6b3c4)
Попробуйте сами придумать еще несколько решений примера 3.
Пример 4. Представить данный одночлен А в виде В", где В — одночлен, если:
а)А = 32a5,n = 5;
б) А = а3b6. n = 3;
в) А =49а2b4c6. n = 2;
г) А = - 27a3b9, n = 3;
д) А = 16a8b5, n = 4;
Решение.
а) Имеем: 32a5 - 25a5 = (2a)5. Значит, А = В5, где В = 2с.
б) Имеем: а3b6 = a3(b2)3 = (ab2)3. Следовательно, А = B3, где B = ab2.
в) Так как 49a2b4c6 =72a2(b2)2(c3)3=(7ab2c3)2
то А=В2 , где В=7ab2c3
г) Поскольку - 27a3b9 = (- 3)3a3(b3)3, заключаем, что А - В3, где В - ЗaЬ3.
д) Имеем: 16a8 =24(a2)4=(2a2)4.
Если бы не было множителя b5, то задача решалась бы без труда:
16a8 = 24(a2)4=(2a2)4
Если бы вместо b5 был множитель b12, то мы решили бы задачу так:
16a8b12 = 24(a2)4(b3)4 =(2a2b3)4
Однако множитель b5 нельзя представить в виде (bk)4, где k — натуральное число, этот множитель, как говорится, «портит все дело». Значит, одночлен
16a8 b5 нельзя представить в виде В4, где В — некоторый одночлен, в Пример показывает, что в математике далеко не все всегда получается, не любая задача имеет решение (как и в реальной жизни).
Кстати, если математику предлагают решить задачу, которая на самом деле не имеет решения, то он говорит: «Задача поставлена некорректно» или «Это — некорректная задача». Тот, кто предложил некорректную задачу, должен извиниться. Вот и автор извиняется за пример 4д). Хотя согласитесь, i что он был дан не без пользы.
Раз уж мы заговорили о корректных и некорректных задачах, приведем еще несколько примеров и тех, и других, а вы попытайтесь объяснить, ' почему задача корректна или некорректна.
Корректные задачи:
1. Упростить 2cb2'CcbK.
2. Упростить 7ab + 8ab + аЬ.
3. Вычислить 2>7 + 3'8 .
4. Представить одночлен 13a4b5 в виде суммы одночленов.
5. Представить одночлен 48х3у*г в виде произведения одно-
членов.
6. Представить одночлен А - 25с4 в виде квадрата некоторого
одночлена В.
Некорректные задачи:
1. Сложить одночлены ЗсЬ2, ЪаЪ2 и 7с2Ь.
2. Вычислить 2'7 + 8'8 .
6-6
3. Представить одночлен А в виде квадрата некоторого одно-
члена В, если А = - 25а4.
4. Представить одночлен А в виде куба некоторого одночлена
В, если А — 8с4.
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|