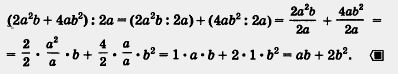|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | ''' ДЕЛЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН ''' |
| - | ''' ДЕЛЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН ''' | + | |
| | | | |
| | <br>Снова, как и в начале § 15, сравним планы построения глав 3 и 4. Вы, наверное, заметили, что эти планы почти одинаковы, хотя полное совпадение нарушил предыдущий параграф (посвященный специфическим формулам сокращенного умножения), да и в главе 3 мы рассмотрели возведение одночлена в степень, а в главе 4 соответствующего разговора о возведении в степень многочлена не было, за исключением случая, когда двучлен возводится в квадрат. После умножения одночленов в главе 3 шла речь о делении одночлена на одночлен. Вот и в главе 4 мы сейчас поговорим об аналогичной операции — делении многочлена на одночлен. | | <br>Снова, как и в начале § 15, сравним планы построения глав 3 и 4. Вы, наверное, заметили, что эти планы почти одинаковы, хотя полное совпадение нарушил предыдущий параграф (посвященный специфическим формулам сокращенного умножения), да и в главе 3 мы рассмотрели возведение одночлена в степень, а в главе 4 соответствующего разговора о возведении в степень многочлена не было, за исключением случая, когда двучлен возводится в квадрат. После умножения одночленов в главе 3 шла речь о делении одночлена на одночлен. Вот и в главе 4 мы сейчас поговорим об аналогичной операции — делении многочлена на одночлен. |
| Строка 13: |
Строка 13: |
| | В ее основе лежит следующее свойство деления суммы на число: <br>(a + b + c):m = (a:m) + (b:m) + (c: m). <br>Это позволяет сразу сформулировать правило деления многочлена на одночлен. | | В ее основе лежит следующее свойство деления суммы на число: <br>(a + b + c):m = (a:m) + (b:m) + (c: m). <br>Это позволяет сразу сформулировать правило деления многочлена на одночлен. |
| | | | |
| - | [[Image:08-06-21.jpg]] | + | [[Image:08-06-21.jpg]] |
| | | | |
| - | В § 12 мы отмечали, что не всегда можно разделить одночлен на одночлен; чтобы деление было выполнимо, необходимо соблюдение целого ряда условий — вспомните их (или посмотрите в § 12), прежде чем рассматривать пример, который приведен ниже. Если задача деления одночлена (простейшего многочлена) на одночлен не всегда была корректной, то что же говорить о делении многочлена на одночлен: такое деление выполнимо достаточно редко. | + | В § 12 мы отмечали, что не всегда можно разделить одночлен на одночлен; чтобы деление было выполнимо, необходимо соблюдение целого ряда условий — вспомните их (или посмотрите в § 12), прежде чем рассматривать пример, который приведен ниже. Если задача деления одночлена (простейшего многочлена) на одночлен не всегда была корректной, то что же говорить о делении многочлена на одночлен: такое деление выполнимо достаточно редко. |
| | | | |
| | <br>'''Пример 1. '''Разделить многочлен 2а<sup>2</sup>b + 4аb<sup>2</sup> на одночлен 2а. <br>Решение. Находим: | | <br>'''Пример 1. '''Разделить многочлен 2а<sup>2</sup>b + 4аb<sup>2</sup> на одночлен 2а. <br>Решение. Находим: |
| | | | |
| - | [[Image:08-06-21.jpg]]<br><br>Здесь мы использовали тот способ записи, кото- <br>рый обговорили в § 12. А вот иной способ (можно <br>применять и тот, и другой, смотря по тому, какой <br>из них вам больше нравится): выделим в каждом <br>члене многочлена 2а2& + 4а&2 множитель, в точнос- <br>ти равный делителю 2а. Получим: <br>2а2& + 4а&2 = 2а • аЪ + 2а • 2&2. <br>Эту сумму можно записать в виде произведения <br>2a(ab + 2Ь2). Теперь ясно, что если это произведение разделить на <br>2а (на один множитель), то в частном получится аЪ + 2Ьг (другой <br>множитель). <br>Пример 2. Разделить многочлен бд:3 - 24л:2 на бд:2. <br>Решение. <br>Первый способ. Находим: <br>(б*3 - 24*2): б*2 = (б*3 : б*2) - B4*2: б*2) = <br>6х3 <br>6хг <br>24*2 6 <br>24 <br><¦ <br>Второй способ. Имеем: <br>б*3 - 24*2 - б*2• х - 6хг • 4 = 6*2(;с - 4). <br>Значит, частное от деления бд:3 - 24а:2 на бд:2 равно х - 4. <br>Пример 3. Разделить многочлен 8а3 + 6а2& - Ъ на 2а2. <br>Решение. Имеем: <br>8а3 + 6а2& - Ъ = 2а2 • 4а + 2а2 -ЗЬ-Ъ. <br>Поскольку в третьем члене заданного многочлена (речь идет о <br>члене -Ь) множитель 2а2 не выделяется, деление невозможно. Эта <br>задача некорректна. Фактически мы снова, как и в конце § 12, <br>пришли к алгебраической дроби — на этот раз к алгебраической <br>8а3+6а2Ь-Ь <br>дроби <br>2а2 <br><¦ <br>Итак, деление многочлена на одночлен выполняется не все- <br>гда, а если и выполняется, то требует определенных усилий. Де- <br>ление же многочлена на многочлен — еще более трудная (и еще <br>более редко выполнимая) операция, это нам пока не по силам. <br><br> | + | [[Image:08-06-21.jpg]]<br><br>Здесь мы использовали тот способ записи, кото- <br>рый обговорили в § 12. А вот иной способ (можно <br>применять и тот, и другой, смотря по тому, какой <br>из них вам больше нравится): выделим в каждом <br>члене многочлена 2а2& + 4а&2 множитель, в точнос- <br>ти равный делителю 2а. Получим: <br>2а2& + 4а&2 = 2а • аЪ + 2а • 2&2. <br>Эту сумму можно записать в виде произведения <br>2a(ab + 2Ь2). Теперь ясно, что если это произведение разделить на <br>2а (на один множитель), то в частном получится аЪ + 2Ьг (другой <br>множитель). <br>Пример 2. Разделить многочлен бд:3 - 24л:2 на бд:2. <br>Решение. <br>Первый способ. Находим: <br>(б*3 - 24*2): б*2 = (б*3 : б*2) - B4*2: б*2) = <br>6х3 <br>6хг <br>24*2 6 <br>24 <br><¦ <br>Второй способ. Имеем: <br>б*3 - 24*2 - б*2• х - 6хг • 4 = 6*2(;с - 4). <br>Значит, частное от деления бд:3 - 24а:2 на бд:2 равно х - 4. <br>Пример 3. Разделить многочлен 8а3 + 6а2& - Ъ на 2а2. <br>Решение. Имеем: <br>8а3 + 6а2& - Ъ = 2а2 • 4а + 2а2 -ЗЬ-Ъ. <br>Поскольку в третьем члене заданного многочлена (речь идет о <br>члене -Ь) множитель 2а2 не выделяется, деление невозможно. Эта <br>задача некорректна. Фактически мы снова, как и в конце § 12, <br>пришли к алгебраической дроби — на этот раз к алгебраической <br>8а3+6а2Ь-Ь <br>дроби <br>2а2 <br><¦ <br>Итак, деление многочлена на одночлен выполняется не все- <br>гда, а если и выполняется, то требует определенных усилий. Де- <br>ление же многочлена на многочлен — еще более трудная (и еще <br>более редко выполнимая) операция, это нам пока не по силам. <br><br> |
| - | | + | |
| | | | |
| | + | <br> |
| | | | |
| | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> | | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> |
Версия 09:11, 8 июня 2010
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Деление многочлена на одночлен
ДЕЛЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН
Снова, как и в начале § 15, сравним планы построения глав 3 и 4. Вы, наверное, заметили, что эти планы почти одинаковы, хотя полное совпадение нарушил предыдущий параграф (посвященный специфическим формулам сокращенного умножения), да и в главе 3 мы рассмотрели возведение одночлена в степень, а в главе 4 соответствующего разговора о возведении в степень многочлена не было, за исключением случая, когда двучлен возводится в квадрат. После умножения одночленов в главе 3 шла речь о делении одночлена на одночлен. Вот и в главе 4 мы сейчас поговорим об аналогичной операции — делении многочлена на одночлен.
В ее основе лежит следующее свойство деления суммы на число:
(a + b + c):m = (a:m) + (b:m) + (c: m).
Это позволяет сразу сформулировать правило деления многочлена на одночлен.
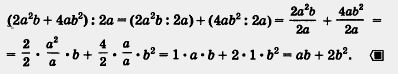
В § 12 мы отмечали, что не всегда можно разделить одночлен на одночлен; чтобы деление было выполнимо, необходимо соблюдение целого ряда условий — вспомните их (или посмотрите в § 12), прежде чем рассматривать пример, который приведен ниже. Если задача деления одночлена (простейшего многочлена) на одночлен не всегда была корректной, то что же говорить о делении многочлена на одночлен: такое деление выполнимо достаточно редко.
Пример 1. Разделить многочлен 2а2b + 4аb2 на одночлен 2а.
Решение. Находим:
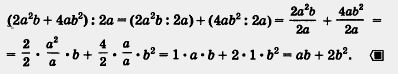
Здесь мы использовали тот способ записи, кото-
рый обговорили в § 12. А вот иной способ (можно
применять и тот, и другой, смотря по тому, какой
из них вам больше нравится): выделим в каждом
члене многочлена 2а2& + 4а&2 множитель, в точнос-
ти равный делителю 2а. Получим:
2а2& + 4а&2 = 2а • аЪ + 2а • 2&2.
Эту сумму можно записать в виде произведения
2a(ab + 2Ь2). Теперь ясно, что если это произведение разделить на
2а (на один множитель), то в частном получится аЪ + 2Ьг (другой
множитель).
Пример 2. Разделить многочлен бд:3 - 24л:2 на бд:2.
Решение.
Первый способ. Находим:
(б*3 - 24*2): б*2 = (б*3 : б*2) - B4*2: б*2) =
6х3
6хг
24*2 6
24
<¦
Второй способ. Имеем:
б*3 - 24*2 - б*2• х - 6хг • 4 = 6*2(;с - 4).
Значит, частное от деления бд:3 - 24а:2 на бд:2 равно х - 4.
Пример 3. Разделить многочлен 8а3 + 6а2& - Ъ на 2а2.
Решение. Имеем:
8а3 + 6а2& - Ъ = 2а2 • 4а + 2а2 -ЗЬ-Ъ.
Поскольку в третьем члене заданного многочлена (речь идет о
члене -Ь) множитель 2а2 не выделяется, деление невозможно. Эта
задача некорректна. Фактически мы снова, как и в конце § 12,
пришли к алгебраической дроби — на этот раз к алгебраической
8а3+6а2Ь-Ь
дроби
2а2
<¦
Итак, деление многочлена на одночлен выполняется не все-
гда, а если и выполняется, то требует определенных усилий. Де-
ление же многочлена на многочлен — еще более трудная (и еще
более редко выполнимая) операция, это нам пока не по силам.
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|