Метод геометрических мест — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Метод геометрических мест

 		Версия 10:00, 18 июня 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад)
← Предыдущая правка
		Текущая версия на 10:18, 18 июня 2012 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
 
		
Строка 1:
Строка 1:
- <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему,  Метод геометрических мест</metakeywords>   + <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Метод геометрических мест, окружность, точка, перпендикулярная прямая</metakeywords>  
  
 '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 7 класс|Математика 7 класс]]&gt;&gt;Математика: Метод геометрических мест'''    '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 7 класс|Математика 7 класс]]&gt;&gt;Математика: Метод геометрических мест'''  
Строка 8:
Строка 8:
 &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Метод геометрических мест. Полные уроки|Метод геометрических мест]]'''    &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Метод геометрических мест. Полные уроки|Метод геометрических мест]]'''  
  
- <br>Сущность метода геометрических мест, используемого при решении задач на построение, состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F<sub>1</sub>, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F<sub>2</sub>. Искомая точка X принадлежит F<sub>1</sub> и F<sub>2</sub>, т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X. Приведем пример.   + <br>Сущность метода геометрических мест, используемого при решении задач на построение, состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. '''[[Геометричне місце точок. Метод геометричних місць|Геометрическое место]]''' точек, удовлетворяющих первому условию, есть некоторая фигура F<sub>1</sub>, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F<sub>2</sub>. Искомая точка X принадлежит F<sub>1</sub> и F<sub>2</sub>, т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и '''[[Окружность|окружностей]]'''), то мы можем их построить и найти интересующую нас точку X. Приведем пример.  
  
 Задача (43). Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В к находится на данном расстоянии от точки С.    Задача (43). Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В к находится на данном расстоянии от точки С.  
  
- Решение. Искомая точка X удовлетворяет двум условиям:   + Решение. Искомая '''[[Точка и прямая|точка]]''' X удовлетворяет двум условиям:  
  
 1) она одинаково удалена от точек А к В;    1) она одинаково удалена от точек А к В;  
Строка 18:
Строка 18:
 2) она находится на данном расстоянии от точки С.    2) она находится на данном расстоянии от точки С.  
  
- Геометрическое место точек, удовлетворяющих первому условию, есть прямая, перпендикулярная отрезку АВ и проходящая через его середину (рис. 106).   + Геометрическое место точек, удовлетворяющих первому условию, есть прямая, '''[[Шпаргалки на тему «Паралельні та перпендикулярні прямі, їх властивості. Доведення від супротивного»|перпендикулярная]]''' отрезку АВ и проходящая через его середину (рис. 106).  
  
 <br>    <br>  
Строка 36:
Строка 36:
  
  
- <sub>Планирование математике, материалы по математике 7 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub>   + <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub>  
  
 <br>    <br>  

Текущая версия на 10:18, 18 июня 2012
 
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Метод геометрических мест 



 
                      Метод геометрических мест 

Сущность метода геометрических мест, используемого при решении задач на построение, состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F₁, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F₂. Искомая точка X принадлежит F₁ и F₂, т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X. Приведем пример. 
Задача (43). Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В к находится на данном расстоянии от точки С. 
Решение. Искомая точка X удовлетворяет двум условиям: 
1) она одинаково удалена от точек А к В; 
2) она находится на данном расстоянии от точки С. 
Геометрическое место точек, удовлетворяющих первому условию, есть прямая, перпендикулярная отрезку АВ и проходящая через его середину (рис. 106). 

 
 

 
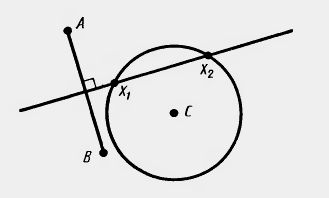
Геометрическое место точек удовлетворяющих второму условию, есть окружность данного радиуса с центром в точке С. Искомая точка X лежит на пересечении этих геометрических мест. 
 



 А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений 
 





 
 _{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать} 

 

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D0%BC%D0%B5%D1%81%D1%82»
@@ Строка 1: / Строка 1: @@
-<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему,  Метод геометрических мест</metakeywords>
+<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 7 класс, Алгебра, урок, на Тему, Метод геометрических мест, окружность, точка, перпендикулярная прямая</metakeywords>
 '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 7 класс|Математика 7 класс]]&gt;&gt;Математика: Метод геометрических мест'''
@@ Строка 8: / Строка 8: @@
 &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; '''[[Метод геометрических мест. Полные уроки|Метод геометрических мест]]'''
-<br>Сущность метода геометрических мест, используемого при решении задач на построение, состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F<sub>1</sub>, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F<sub>2</sub>. Искомая точка X принадлежит F<sub>1</sub> и F<sub>2</sub>, т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X. Приведем пример.
+<br>Сущность метода геометрических мест, используемого при решении задач на построение, состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X, удовлетворяющую двум условиям. '''[[Геометричне місце точок. Метод геометричних місць|Геометрическое место]]''' точек, удовлетворяющих первому условию, есть некоторая фигура F<sub>1</sub>, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F<sub>2</sub>. Искомая точка X принадлежит F<sub>1</sub> и F<sub>2</sub>, т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и '''[[Окружность|окружностей]]'''), то мы можем их построить и найти интересующую нас точку X. Приведем пример.
 Задача (43). Даны три точки: А, В, С. Постройте точку X, которая одинаково удалена от точек А и В к находится на данном расстоянии от точки С.
-Решение. Искомая точка X удовлетворяет двум условиям:
+Решение. Искомая '''[[Точка и прямая|точка]]''' X удовлетворяет двум условиям:
 ) она одинаково удалена от точек А к В;
@@ Строка 18: / Строка 18: @@
 ) она находится на данном расстоянии от точки С.
-Геометрическое место точек, удовлетворяющих первому условию, есть прямая, перпендикулярная отрезку АВ и проходящая через его середину (рис. 106).
+Геометрическое место точек, удовлетворяющих первому условию, есть прямая, '''[[Шпаргалки на тему «Паралельні та перпендикулярні прямі, їх властивості. Доведення від супротивного»|перпендикулярная]]''' отрезку АВ и проходящая через его середину (рис. 106).
 <br>
@@ Строка 36: / Строка 36: @@
-<sub>Планирование математике, материалы по математике 7 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub>
+<br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub>
 <br>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: