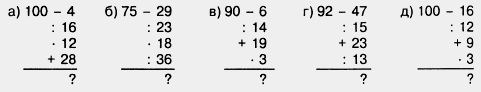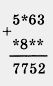|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Степень числа, Квадрат, куб числа</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 5 класс, Алгебра, урок, на Тему, Степень числа, Квадрат, куб числа, число, уравнения, цифры, задачи, выражение, квадратом числа, натуральных чисел</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Степень числа. Квадрат и куб числа''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Степень числа. Квадрат и куб числа''' |
| Строка 8: |
Строка 8: |
| | <br>Мы знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче — в виде произведения. Например, вместо 3 + 3 + 3 + 3 + 3 пишут 3 • 5. В этом произведении число 5 показывает, сколько слагаемых было в [http://xvatit.com/busines/ '''сумме''']. | | <br>Мы знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче — в виде произведения. Например, вместо 3 + 3 + 3 + 3 + 3 пишут 3 • 5. В этом произведении число 5 показывает, сколько слагаемых было в [http://xvatit.com/busines/ '''сумме''']. |
| | | | |
| - | Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют основанием степени, число 6, которое показывает, сколько множителей было в произведении, — показателем степени, а выражение 26 называют степенью. | + | Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют основанием степени, '''[[Додавання і віднімання натуральних чисел|число]]''' 6, которое показывает, сколько множителей было в произведении, — показателем степени, а выражение 26 называют степенью. |
| | | | |
| | '''Пример 1.''' Запишем произведения в виде степени и найдем их значения: <br> | | '''Пример 1.''' Запишем произведения в виде степени и найдем их значения: <br> |
| Строка 14: |
Строка 14: |
| | 3 • 3 • 3 • 3 = 34 = 81; <br>5 . 5 • 5 = 53= 125; <br>2 • 2 • 2 • 2 • 2 • 2 = 26 = 64. <br> | | 3 • 3 • 3 • 3 = 34 = 81; <br>5 . 5 • 5 = 53= 125; <br>2 • 2 • 2 • 2 • 2 • 2 = 26 = 64. <br> |
| | | | |
| - | торую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З<sup>2</sup>. <br>Произведение n и n называют квадратом числа n и обозначают n2 (читают: «эн в квадрате»). Итак, n<sup>2</sup> = n • n.
| + | Которую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З<sup>2</sup>. <br>Произведение n и n называют '''[[Множення натуральних чисел. Квадрат і куб числа. Презентація уроку|квадратом числа]]''' n и обозначают n2 (читают: «эн в квадрате»). Итак, n<sup>2</sup> = n • n. |
| | | | |
| | Например, 172 = 17 • 17 = 289. <br> | | Например, 172 = 17 • 17 = 289. <br> |
| Строка 28: |
Строка 28: |
| | Например, 8<sup>3</sup> = 8 •8 •8 = 64-8 = 512. | | Например, 8<sup>3</sup> = 8 •8 •8 = 64-8 = 512. |
| | | | |
| - | Таблица кубов первых 10 натуральных чисел имеет вид: <br> | + | Таблица кубов первых 10 '''[[Обозначение натуральных чисел|натуральных чисел]]''' имеет вид: <br> |
| | | | |
| | [[Image:16-06-2.jpg|480px|Задание]]<br><br>Первую степень числа считают равной самому числу: | | [[Image:16-06-2.jpg|480px|Задание]]<br><br>Первую степень числа считают равной самому числу: |
| Строка 36: |
Строка 36: |
| | Показатель степени 1 обычно не пишут. | | Показатель степени 1 обычно не пишут. |
| | | | |
| - | Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий. | + | Если в числовое '''[[Повторення таблиць додавання і віднімання. Складання виразів за текстовим формулюванням|выражение]]''' входят степени чисел, то их значения вычисляют до выполнения остальных действий. |
| | | | |
| | '''Пример 2.''' Найдем значение выражения (4 + З)<sup>2</sup> • 5<sup>2</sup> - 8<sup>3</sup> + 2<sup>6</sup>. | | '''Пример 2.''' Найдем значение выражения (4 + З)<sup>2</sup> • 5<sup>2</sup> - 8<sup>3</sup> + 2<sup>6</sup>. |
| Строка 84: |
Строка 84: |
| | [[Image:16-06-3.jpg|480px|Задание]]<br> | | [[Image:16-06-3.jpg|480px|Задание]]<br> |
| | | | |
| - | <br>660. Угадайте корни уравнения: <br> | + | <br>660. Угадайте корни '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнения]]''': <br> |
| | | | |
| | а) х • х = 25; в) а • а = 1; <br>б) у • у = 81; г)Ь•Ь•Ь = 0.<br> | | а) х • х = 25; в) а • а = 1; <br>б) у • у = 81; г)Ь•Ь•Ь = 0.<br> |
| | | | |
| - | 661. Какие цифры заменены звездочками? <br> | + | 661. Какие '''[[Ілюстрації: Лічба предметів. Порівняння предметів за величиною. Підготовчі вправи до написання цифр.|цифры]]''' заменены звездочками? <br> |
| | | | |
| | [[Image:16-06-4.jpg|80px|Задание]]<br>Подумайте, какие уравнения пришлось решать для нахождения 7752 неизвестных цифр. <br> | | [[Image:16-06-4.jpg|80px|Задание]]<br>Подумайте, какие уравнения пришлось решать для нахождения 7752 неизвестных цифр. <br> |
| Строка 136: |
Строка 136: |
| | 14 • (3600 • 18 - 239 200 : 46). <br> | | 14 • (3600 • 18 - 239 200 : 46). <br> |
| | | | |
| - | Выдающийся российский [http://xvatit.com/vuzi/ '''математик'''] академик Андреи Николаевич Колмогоров решил много сложнейших задач, совершил не одно открытие в различных разделах современной математики. Но радость своих первых математических «открытий» он познал рано. Андрей Николаевич рассказывал, что еще до поступления в гимназию в возрасте пяти-шести лет он любил придумывать задачи, подмечал интересные свойства чисел. Эти «открытия» публиковались в домашнем журнале. Вот одно из «открытий» шестилетнего Колмогорова. Он заметил, что <br> | + | Выдающийся российский [http://xvatit.com/vuzi/ '''математик'''] академик Андреи Николаевич Колмогоров решил много сложнейших задач, совершил не одно открытие в различных разделах современной математики. Но радость своих первых математических «открытий» он познал рано. Андрей Николаевич рассказывал, что еще до поступления в гимназию в возрасте пяти-шести лет он любил придумывать '''[[Практичне завдання до теми Додавання та віднімання чисел в межах 10 Поняття вартість монет|задачи]]''', подмечал интересные свойства чисел. Эти «открытия» публиковались в домашнем журнале. Вот одно из «открытий» шестилетнего Колмогорова. Он заметил, что <br> |
| | | | |
| | 1<sup>2</sup> = 1, 2<sup>2</sup> = 1+3, 3<sup>2</sup> = 1+3 + 5, 4<sup>2</sup> = 1+3 + 5 + 7. | | 1<sup>2</sup> = 1, 2<sup>2</sup> = 1+3, 3<sup>2</sup> = 1+3 + 5, 4<sup>2</sup> = 1+3 + 5 + 7. |
Текущая версия на 08:57, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Степень числа. Квадрат и куб числа
Степень числа. Квадрат и куб числа
Мы знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче — в виде произведения. Например, вместо 3 + 3 + 3 + 3 + 3 пишут 3 • 5. В этом произведении число 5 показывает, сколько слагаемых было в сумме.
Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют основанием степени, число 6, которое показывает, сколько множителей было в произведении, — показателем степени, а выражение 26 называют степенью.
Пример 1. Запишем произведения в виде степени и найдем их значения:
3 • 3 • 3 • 3 = 34 = 81;
5 . 5 • 5 = 53= 125;
2 • 2 • 2 • 2 • 2 • 2 = 26 = 64.
Которую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З2.
Произведение n и n называют квадратом числа n и обозначают n2 (читают: «эн в квадрате»). Итак, n2 = n • n.
Например, 172 = 17 • 17 = 289.
Таблица квадратов первых 10 натуральных чисел имеет следующий вид:

Третья степень числа также имеет и иное название. Произведение 4 • 4 • 4 называют кубом числа 4 и обозначают 43. Произведение n • n • n называют кубом числа n и обозначают n3 (читают: 5 «эн в кубе»).
Итак, n3 = n • n • n.
Например, 83 = 8 •8 •8 = 64-8 = 512.
Таблица кубов первых 10 натуральных чисел имеет вид:

Первую степень числа считают равной самому числу:
71 = 7, 161 = 16, 11 = 1.
Показатель степени 1 обычно не пишут.
Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.
Пример 2. Найдем значение выражения (4 + З)2 • 52 - 83 + 26.
Решение.
(4 + З)2 • 52 - 83 + 26 = 72 - 25 - 512 + 64= 49 • 25 - 512 + 64 = 1225 - 512 + 64 = 777.
Что такое квадрат числа?
Что такое куб числа?
Назовите основание и показатель степени: б7, 123, 410, 152, 81.
652. Составьте таблицу квадратов чисел от 11 до 20.
653. Представьте в виде степени произведение:
а) 6 • 6 • 6 • 6 • 6 • 6 • 6;
в) 73 • 73;
б) 25 • 25 • 25 • 25 • 25;
г) 11 • 11 • 11 • 11;
д) 9 • 9 • 9;
е) m• m • m • m • m • m;
ж) х • х • х;
з) у• у •у• у• у• у• у •у;
и) k • к
к) n • n • n •n • n;
л) (х + 1)(х + 1)(х + 1);
м) (7 - n)(7 - n).
654. Представьте в виде произведения степень:
а) 75; г) 10002; ж) k3; к) (m + 2)4;
б) 124; д) 607; з) а8; л) (а - 7)2;
в) 153; е) n9; и) х2; м) (х 4- у)3.
655. Найдите значения: 252; 1002; 103; II3; 123; 153.
656. Найдите значения степеней: 25; 106; I20; З4; 411; 44.
657. Найдите значение выражения:
а) З2 • 18; д) 7 + 43; и) 52 • 23;
б) 5 + 42; е) 73 + 4; к) 25 + З4;
в) (5 + 4)2; ж) (7 + 4)3; л) (30 : З)5 - 1003;
г) 52 + 42; з) (73 - 43) : (7 - 4); м) (102 - 26) : 6 + 110.
658. Пользуясь таблицами квадратов и кубов чисел, найдите значение д, если:
121 - n2; n2 = 196; n2 = 10 000; 125 = n3; n3 = 512.
659. Вычислите устно:
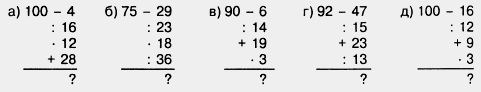
660. Угадайте корни уравнения:
а) х • х = 25; в) а • а = 1;
б) у • у = 81; г)Ь•Ь•Ь = 0.
661. Какие цифры заменены звездочками?
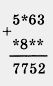
Подумайте, какие уравнения пришлось решать для нахождения 7752 неизвестных цифр.
662. Каков порядок выполнения действий при вычислении значения выражения:
а) 160 + 37 - 20;
б) 90 - 60 : 15;
в) 80 - 15 + 25?
Если возможно, укажите другой порядок действий, приводящий к тому же результату.
663. Составьте выражение по следующей программе:
1. Разделить 58 344 на 429.
2. 215 умножить на 48.
3. Сложить результаты команд 1 и 2.
Найдите значение получившегося выражения.
664. Составьте схему вычисления выражения:
(39 • 71 + 25 • 95) - (248 : 4 - 176 : 11).
665. Решите задачу:
1) Сумма двух чисел 549. Одно из них в 8 раз больше другого. Найдите эти числа.
2) Сумма двух чисел 378. Одно из них в 8 раз меньше другого. Найдите эти числа.
3) Разность двух чисел 342. Одно из них в 7 раз меньше другого. Найдите эти числа.
4) Разность двух чисел 516. Одно из них в 7 раз больше другого. Найдите эти числа.
666. Найдите значения:
182; 53; 132; 203; 402; 303.
667. Найдите значения: 24; З3; 105; 112; 1004; 206.
668. Найдите значение выражения:
а) 92 + 19; е) (17 - 16)8 + 25;
б) 172 - 209; ж) 106 - 204;
в) б3 : 3; з) З4 • 104;
г) 23 • З2; и) 54 : 52.
д) (15 - 7)2 : 23;
669. Из Москвы и Ростова-на-Дону одновременно вышли навстречу друг другу два поезда. Поезд из Москвы шел со скоростью 65 км/ч, а поезд из Ростова-на-Дону — со скоростью на 7 км/ч меньшей. На каком расстоянии друг от друга будут поезда через 6 ч после начала движения, если расстояние между Москвой и Ростовом-на-Дону 1230 км?
670. С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 75 км/ч, а скорость второго на 10 км/ч больше. На каком расстоянии друг от друга будут поезда через 4 ч?
671. Составьте программу вычислений для нахождения значения выражения
67 392 : (3504 - 3408) + 19 232 : 601
и изобразите ее схемой. Найдите значение выражения.
672. Выполните действия:
14 • (3600 • 18 - 239 200 : 46).
Выдающийся российский математик академик Андреи Николаевич Колмогоров решил много сложнейших задач, совершил не одно открытие в различных разделах современной математики. Но радость своих первых математических «открытий» он познал рано. Андрей Николаевич рассказывал, что еще до поступления в гимназию в возрасте пяти-шести лет он любил придумывать задачи, подмечал интересные свойства чисел. Эти «открытия» публиковались в домашнем журнале. Вот одно из «открытий» шестилетнего Колмогорова. Он заметил, что
12 = 1, 22 = 1+3, 32 = 1+3 + 5, 42 = 1+3 + 5 + 7.
673. Попробуйте рассказать, что это за свойство. Проверьте, выполняется ли оно для квадратов нескольких следующих чисел.
Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека. Таковы сажень, локоть, пядь. В Англии и США до сих пор используется «ступня» — фут (31 см), «большой палеи,» — дюйм (25 мм) и даже ярд (91 см) — единица длины, появившаяся почти 900 лет назад.
Она была равна расстоянию от кончика носа короля Генриха I до конца пальцев его вытянутой руки.
Для измерения больших расстояний на Руси использовали единииу пoприще, замененную позже верстбй (в разных местностях версту считали по-разному — от 500 до 750 сажен).
От восточных купцов пошла единица аршин (тоже означает «локоть») — существовали турецкий аршин, персидский аршин и др. Поэтому и возникла по-
говорка «мерить на свой аршин».
Множество единиц существовало и для измерения массы. Наиболее древняя русская мера — гривна, или гривенка (около 410 г). Позднее появились золотники, фунты, пуды.
В связи с развитием торговли назрела необходимость установить четкие определения единиц и соотношения между ними. При Петре I русские меры были приведены в определенную систему:
1 верста = 500 саженям (1 км 67 м);
1 сажень = 3 аршинам (2131см);
1 аршин = 16 вершкам = 28 дюймам (71 см);
1 фут = 12 дюймам (30 см 5 мм):
1 пуд = 40 фунтам (гривенкам) (16 кг 400 г);
1 фунт = 96 золотникам (410 г).
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Книги и учебники согласно календарному плануванння по математике 5 класса скачать, помощь школьнику онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|