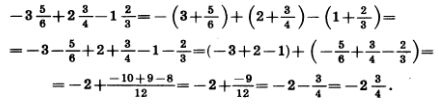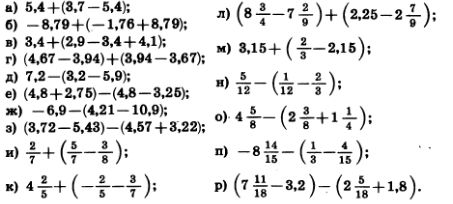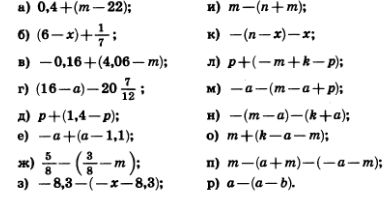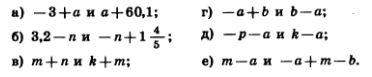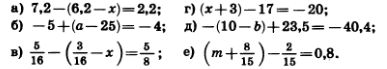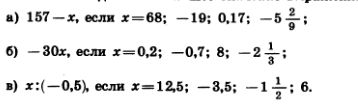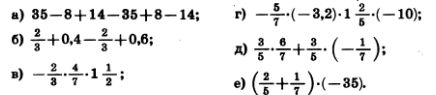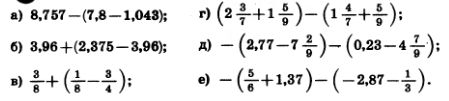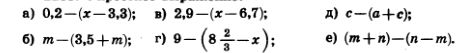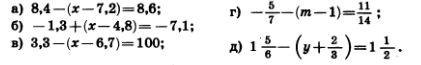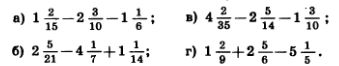|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Раскрытие скобок</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 6 класс, Алгебра, урок, на Тему, Раскрытие скобок, Выражение, числа, сложения, дробные, уравнение, координаты, пропорции</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Раскрытие скобок''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Раскрытие скобок''' |
| Строка 7: |
Строка 7: |
| | '''39. Раскрытие скобок''' | | '''39. Раскрытие скобок''' |
| | | | |
| - | <br>Выражение а+(b + с) можно записать без скобок: a+(b + c)=a + b + c. Эту операцию называют раскрытием скобок.<br> | + | <br>'''[[Основное свойство алгебраической дроби|Выражение]]''' а+(b + с) можно записать без скобок: a+(b + c)=a + b + c. Эту операцию называют раскрытием скобок.<br> |
| | | | |
| | '''Пример 1. '''Раскроем скобки в выражении а + ( — b + c). | | '''Пример 1. '''Раскроем скобки в выражении а + ( — b + c). |
| Строка 19: |
Строка 19: |
| | '''Решение.''' Раскрывая скобки, получим - 2,87 + (2,87 - 7,639) = — - 2,87 + 2,87 - 7,639 =0 — 7,639 = - 7,639.<br> | | '''Решение.''' Раскрывая скобки, получим - 2,87 + (2,87 - 7,639) = — - 2,87 + 2,87 - 7,639 =0 — 7,639 = - 7,639.<br> |
| | | | |
| - | Чтобы найти значение выражения — (— 9 + 5), надо сложить числа —9 и 5 и найти число, противоположное полученной сумме: —( — 9 + 5)= —( — 4) = 4. | + | Чтобы найти значение выражения — (— 9 + 5), надо сложить '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|числа]]''' —9 и 5 и найти число, противоположное полученной сумме: —( — 9 + 5)= —( — 4) = 4. |
| | | | |
| | То же значение можно получить по-другому: вначале записать числа, противоположные данным слагаемым (т. е. изменить их знаки), а потом сложить: 9 + ( — 5) = 4. Таким образом, —( — 9 + 5) = 9 — 5 = 4.<br> | | То же значение можно получить по-другому: вначале записать числа, противоположные данным слагаемым (т. е. изменить их знаки), а потом сложить: 9 + ( — 5) = 4. Таким образом, —( — 9 + 5) = 9 — 5 = 4.<br> |
| Строка 37: |
Строка 37: |
| | '''Решение.''' 9,36 - (9,36 - 5,48) = 9,36 + (- 9,36 + 5,48) = = 9,36 — 9,36 + 5,48 = 0 -f 5,48 = 5,48.<br> | | '''Решение.''' 9,36 - (9,36 - 5,48) = 9,36 + (- 9,36 + 5,48) = = 9,36 — 9,36 + 5,48 = 0 -f 5,48 = 5,48.<br> |
| | | | |
| - | Раскрытие скобок и применение переместительного и сочетательного свойств сложения позволяют упрощать вычисления. | + | Раскрытие скобок и применение переместительного и сочетательного свойств '''[[Метод алгебраического сложения|сложения]]''' позволяют упрощать вычисления. |
| | | | |
| | '''Пример 5.''' Найдем значение выражения (—4—20)+(6+13)—(7—8)—5. | | '''Пример 5.''' Найдем значение выражения (—4—20)+(6+13)—(7—8)—5. |
| Строка 49: |
Строка 49: |
| | [[Image:2010-120.jpg|160px|Задание]] | | [[Image:2010-120.jpg|160px|Задание]] |
| | | | |
| - | '''Решение.'''Сначала представим каждое слагаемое в виде суммы их целой и дробной частей, затем раскроем скобки, потом сложим отдельно целые и отдельно дробные части и, наконец, сложим полученные результаты: | + | '''Решение.'''Сначала представим каждое слагаемое в виде суммы их целой и дробной частей, затем раскроем скобки, потом сложим отдельно целые и отдельно '''[[Фішки для допитливих до уроку: Дробові числа. Звичайні дроби.|дробные]]''' части и, наконец, сложим полученные результаты: |
| | | | |
| | [[Image:2010-121.jpg|480px|Задание]]<br>[[Image:2010-09.jpg]]Как раскрывают скобки, перед которыми стоит знак « + »? Как можно найти значение выражения, противоположное сумме нескольких чисел? Как раскрыть скобки, перед которыми стоит знак « — »?<br> | | [[Image:2010-121.jpg|480px|Задание]]<br>[[Image:2010-09.jpg]]Как раскрывают скобки, перед которыми стоит знак « + »? Как можно найти значение выражения, противоположное сумме нескольких чисел? Как раскрыть скобки, перед которыми стоит знак « — »?<br> |
| Строка 75: |
Строка 75: |
| | [[Image:2010-125.jpg|480px|Задание]] | | [[Image:2010-125.jpg|480px|Задание]] |
| | | | |
| - | <br>1225. Решите уравнение: | + | <br>1225. Решите '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''': |
| | | | |
| | [[Image:2010-126.jpg|480px|Задание]] | | [[Image:2010-126.jpg|480px|Задание]] |
| Строка 101: |
Строка 101: |
| | а) меньшее из них равно —12; в) меньшее из них равно n;<br>б) большее из них равно —18; г) большее из них равно k. | | а) меньшее из них равно —12; в) меньшее из них равно n;<br>б) большее из них равно —18; г) большее из них равно k. |
| | | | |
| - | 1231. Найдите координаты середины отрезка, если координаты его концов равны: | + | 1231. Найдите '''[[Шкалы и координаты|координаты]]''' середины отрезка, если координаты его концов равны: |
| | | | |
| | [[Image:2010-130.jpg|480px|Задание]]<br>1232. Каким числом будет значение выражения x + y, если: | | [[Image:2010-130.jpg|480px|Задание]]<br>1232. Каким числом будет значение выражения x + y, если: |
| Строка 113: |
Строка 113: |
| | 1234. Найдите значение выражения:<br>[[Image:2010-131.jpg|480px|Задание]]<br>1235. Представьте:<br>а) в виде десятичных дробей: [[Image:2010-132.jpg|Задание]]<br>б) в виде обыкновенных дробей: 1,2; 3,25; 0,75; 1,125. | | 1234. Найдите значение выражения:<br>[[Image:2010-131.jpg|480px|Задание]]<br>1235. Представьте:<br>а) в виде десятичных дробей: [[Image:2010-132.jpg|Задание]]<br>б) в виде обыкновенных дробей: 1,2; 3,25; 0,75; 1,125. |
| | | | |
| - | 1236. Найдите неизвестный член пропорции:<br>[[Image:2010-133.jpg|320px|Задание]]<br>[[Image:2010-09d.jpg]] 1238. Раскройте скобки и найдите значение выражения:<br>[[Image:2010-134.jpg|480px|Задание]] | + | 1236. Найдите неизвестный член '''[[Фішки для допитливих до уроку на тему «Пропорція»|пропорции]]''':<br>[[Image:2010-133.jpg|320px|Задание]]<br>[[Image:2010-09d.jpg]] 1238. Раскройте скобки и найдите значение выражения:<br>[[Image:2010-134.jpg|480px|Задание]] |
| | | | |
| | <br>1239. Упростите выражение: | | <br>1239. Упростите выражение: |
Текущая версия на 17:47, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Раскрытие скобок
39. Раскрытие скобок
Выражение а+(b + с) можно записать без скобок: a+(b + c)=a + b + c. Эту операцию называют раскрытием скобок.
Пример 1. Раскроем скобки в выражении а + ( — b + c).
Решение. a + (-b+c) = a + ((-b) + c)=a + (-b) + c = a-b + c.
Если перед скобками стоит знак « + » то можно опустить скобки и этот знак « + » сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком « + ».
Пример 2. Найдем значение выражения -2,87+ (2,87-7,639).
Решение. Раскрывая скобки, получим - 2,87 + (2,87 - 7,639) = — - 2,87 + 2,87 - 7,639 =0 — 7,639 = - 7,639.
Чтобы найти значение выражения — (— 9 + 5), надо сложить числа —9 и 5 и найти число, противоположное полученной сумме: —( — 9 + 5)= —( — 4) = 4.
То же значение можно получить по-другому: вначале записать числа, противоположные данным слагаемым (т. е. изменить их знаки), а потом сложить: 9 + ( — 5) = 4. Таким образом, —( — 9 + 5) = 9 — 5 = 4.
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
Значит, — (а + b) = — а — b.
Пример 3. Найдем значение выражения 16 — (10 —18 + 12).
Решение. 16—(10 —18 + 12) = 16 + ( —(10 —18 + 12)) = = 16 + (-10 +18-12) = 16-10 +18-12 = 12.
Чтобы раскрыть скобки, перед которыми стоит знак «—», надо заменить этот знак на « + », поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Пример 4. Найдем значение выражения 9,36—(9,36 — 5,48).
Решение. 9,36 - (9,36 - 5,48) = 9,36 + (- 9,36 + 5,48) = = 9,36 — 9,36 + 5,48 = 0 -f 5,48 = 5,48.
Раскрытие скобок и применение переместительного и сочетательного свойств сложения позволяют упрощать вычисления.
Пример 5. Найдем значение выражения (—4—20)+(6+13)—(7—8)—5.
Решение. Сначала раскроем скобки, а потом найдем отдельно сумму всех положительных и отдельно сумму всех отрицательных чисел и, наконец, сложим полученные результаты:
( — 4 — 20)+(6+ 13)—(7 — 8) — 5 = —4—20 + 6 + 13—7 + 8—5 = = (6 + 13 + 8)+( — 4 — 20 — 7 — 5)= 27—36=—9.
Пример 6. Найдем значение выражения
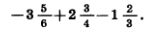
Решение.Сначала представим каждое слагаемое в виде суммы их целой и дробной частей, затем раскроем скобки, потом сложим отдельно целые и отдельно дробные части и, наконец, сложим полученные результаты:
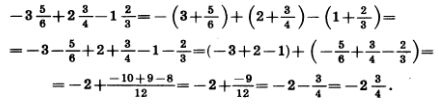
 Как раскрывают скобки, перед которыми стоит знак « + »? Как можно найти значение выражения, противоположное сумме нескольких чисел? Как раскрыть скобки, перед которыми стоит знак « — »? Как раскрывают скобки, перед которыми стоит знак « + »? Как можно найти значение выражения, противоположное сумме нескольких чисел? Как раскрыть скобки, перед которыми стоит знак « — »?
 1218. Раскройте скобки: 1218. Раскройте скобки:
а) 3,4+(2,6+ 8,3); в) m+(n-k);
б) 4,57+(2,6 — 4,57); г) с+(-a + b).
1219. Найдите значение выражения:
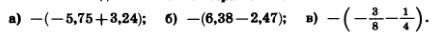
1220. Раскройте скобки:
а) 85+(7,8+ 98); г) -(80-16) + 84; ж) a-(b-k-n);
б) (4,7 —17)+7,5; д) -а + (m-2,6); з) -(а-b + с);
в) 64—(90 + 100); е) с+(— а-b); и) (m-n)—(p-k).
1221. Раскройте скобки и найдите значение выражения:
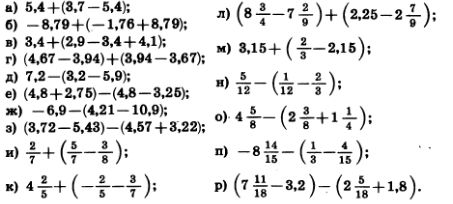
1222. Упростите выражение:
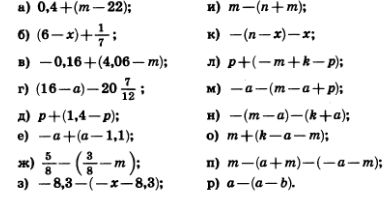
1223. Напишите сумму двух выражений и упростите ее:
а) — 4 — m и m + 6,4; г) а+b и р — b
б) 1,1+а и —26—а; д) — m + n и —k — n;
в) а + 13 и —13 + b; е)m — n и n — m.
1224. Напишите разность двух выражений и упростите ее:
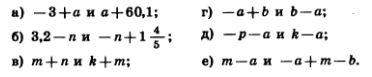
1225. Решите уравнение:
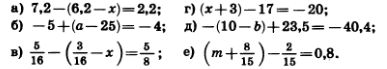
1226. Решите с помощью уравнения задачу:
а) На одной полке 42 книги, а на другой 34. Со второй полки сняли несколько книг, а с первой — столько, сколько осталось на второй. После этого на первой полке осталось 12 книг. Сколько книг сняли со второй полки?
б) В первом классе 42 ученика, во втором на 3 ученика меньше, чем в третьем. Сколько учеников в третьем классе, если всего в этих трех классах 125 учеников?
1227. Найдите значение выражения:

 1228. Вычислите устно: 1228. Вычислите устно:
1229. Найдите наибольшее значение выражения:
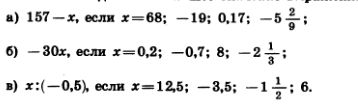
1230. Укажите 4 последовательных целых числа, если:
а) меньшее из них равно —12; в) меньшее из них равно n;
б) большее из них равно —18; г) большее из них равно k.
1231. Найдите координаты середины отрезка, если координаты его концов равны:
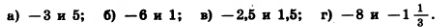
1232. Каким числом будет значение выражения x + y, если:
а) x>0, у>0; в) x>0, ус0; д) x>0, у=0;
б) x<0, у<0; г) x=0, у<0; е) x=0, у=0?
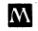 1233. Решите с помощью графа задачу: «Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, белое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля — в синем, Люба — в белом; 2) Оля — в красном, Нина — в синем; 3) Вера — в синем, Люба в голубом. В каждом ответе только одна часть верна, а остальные нет. Какого цвета платье надела каждая девочка? 1233. Решите с помощью графа задачу: «Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, белое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля — в синем, Люба — в белом; 2) Оля — в красном, Нина — в синем; 3) Вера — в синем, Люба в голубом. В каждом ответе только одна часть верна, а остальные нет. Какого цвета платье надела каждая девочка?
1234. Найдите значение выражения:
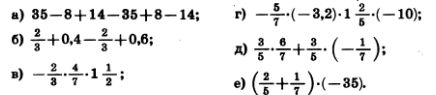
1235. Представьте:
а) в виде десятичных дробей: 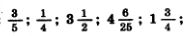
б) в виде обыкновенных дробей: 1,2; 3,25; 0,75; 1,125.
1236. Найдите неизвестный член пропорции:
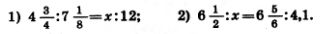
 1238. Раскройте скобки и найдите значение выражения: 1238. Раскройте скобки и найдите значение выражения:
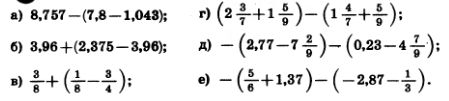
1239. Упростите выражение:
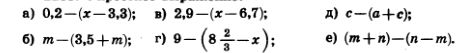
1240. Решите уравнение:
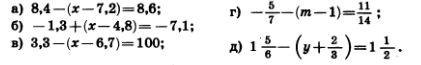
1241. Найдите значение выражения:
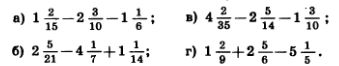
1242. Решите задачу, составив пропорцию:
а) Затрачивая на изготовление каждой детали 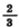 ч, бригада выпускала за смену 540 деталей. Сколько деталей будет выпускать за смену бригада, если на изготовление каждой детали будут затрачивать ч, бригада выпускала за смену 540 деталей. Сколько деталей будет выпускать за смену бригада, если на изготовление каждой детали будут затрачивать 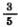 ч? На сколько процентов повысится при этом производительность труда? ч? На сколько процентов повысится при этом производительность труда?
б) Масса 15 л керосина 12,3 кг. Какова масса 35 л керосина?
в) Из 0,3 т свежих яблок получается 57 кг сушеных. Сколько сушеных яблок получится из 5,5 т свежих?
1243. Решите уравнение:
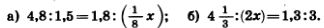
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Планы конспектов уроков по математике 6 класса скачать, учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|